
Универсальные направления: кодирование многоплоскости динамики решетки в квантовых системах
17 июня 2025 г.Таблица ссылок
Введение
Решетчатые модели и координировать пространство
Кодирование государствам кубита
3.1 Кодирование структуры решетки в QUBIT STA
3.2 Выбор плоскости поворота
3.3 Распространение его на другие структуры
Выводы и ссылки
2 модели решетки и координировать пространство
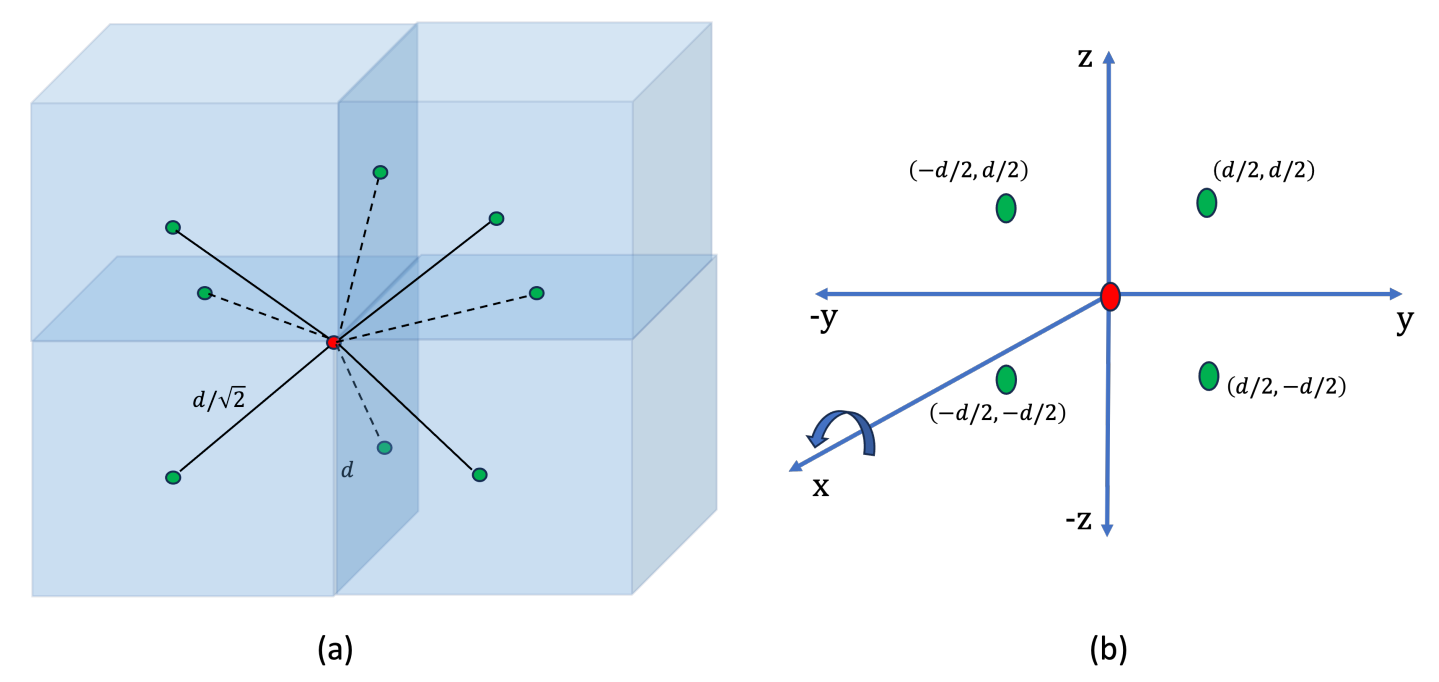
Рис. 2 (а) дает раздел структуры решетки FCC. Учитывая белковый бусин на начале координат, мы хотели бы узнать возможный набор 3D -координат, которые может занять следующий шарик после поворота. Рис. 2 (b) дает возможные координаты в данной плоскостиy - z.

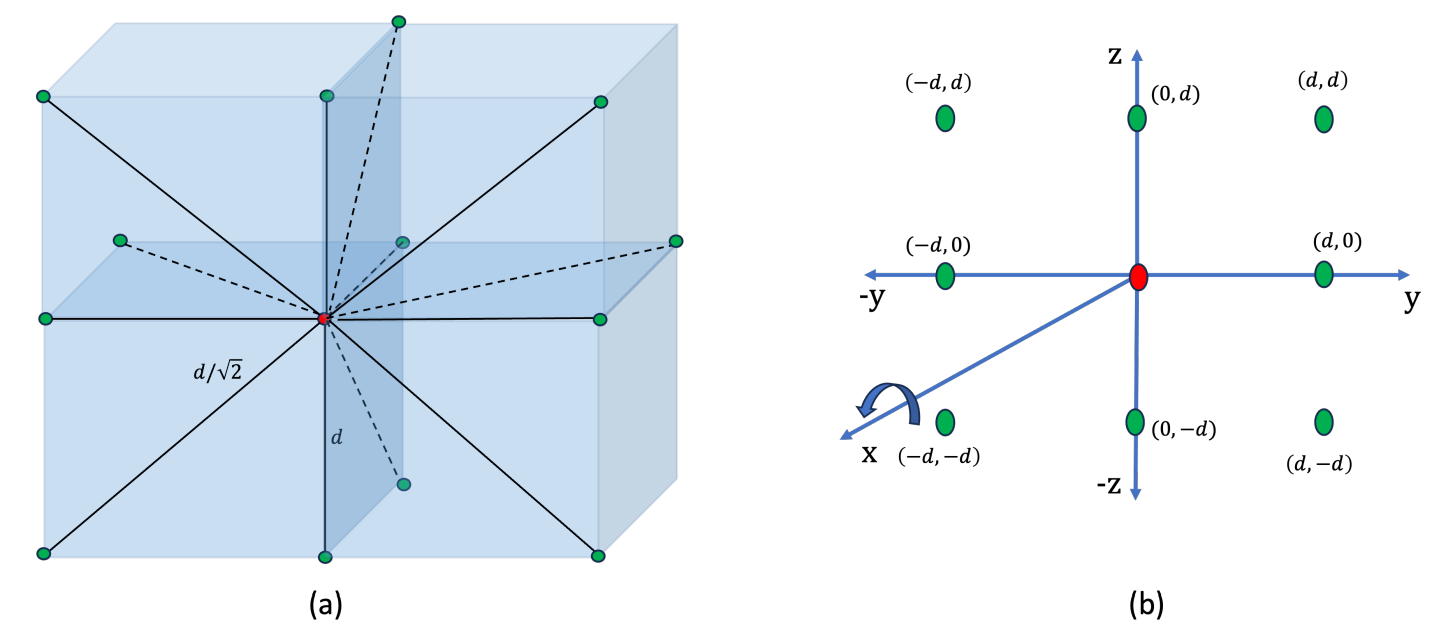
Теперь давайте посмотрим на кубическую решетку с плоскими диагоналами. Рис. 3 (а) дает раздел кубической решетки, а 3 (b) дает картирование координат. В кубической решетке повороты могут быть в 8 направлениях в данной плоскости. С 3 самолетами есть 24 возможных поворотов. Однако для каждого набора двух плоскостей есть два направления, которые повторяются. Например, если мы рассмотрим плоскость x - y и плоскость y -z, направления ± y повторяются. В результате у нас будет 6 таких плоскостей, которые повторяются. В целом, у нас будет 24 - 6 = 18 градусов свободы здесь.
Чтобы кодировать, нам нужно сопоставить состояния кубита с координатами бисера. Давайте рассмотрим решетку FCC. Мы можем начать с происхождения как координаты первой бусинки. Вторая бусинка займет положение на любой из вершин или грани, как показано на рис. 2 (б). Если мы обозначим оси как x, y и z, местоположение второго шарика может быть в любой из плоскостей XY, YZ или ZX. Красная бусинка на начале. Если второй шарик должен был быть в плоскости Y - Z, возможные координаты, которые он мог иметь, показаны на рисунке. Координаты - это координаты Y и Z, данные как (Y, Z). Это вращение вокруг оси X с интервалом 90 ° для 4 различных точек, в направлении против часовой стрелки. Мы увидим аналогичный набор координат в плоскости z - x и x - y, если бы второй шарик должен был быть в этих плоскостях. На рис. 2 (б) x координаты красных и зеленых бусин одинаковы. Мы могли бы перенести эту логику в каждый шарик в последовательности белка. Если мы рассмотрим какой -либо бусин I с координатами (x, y, z), бусин i + 1 будет тогда иметь координаты (x + ∆x, y + ∆y, z + ∆z). Если шарик I + 1 находится в плоскости, параллельной плоскости Y - Z, ∆x = 0 и ∆y и ∆Z будут принимать значения, как показано на рис. 2 (b). Если он находится в плоскости, параллельной плоскости z-x (вращение против часовой стрелки вокруг оси y), ∆Z и ∆x будут принимать те же значения, что и ∆y и ∆Z в предыдущем случае, и в том же порядке. Точно так же, когда шарик I + 1 находится в плоскости, параллельной плоскости x-Y (вращение против часовой стрелки вокруг оси Z), ∆x и ∆y будут принимать одинаковые значения.

Точно так же, с кубической решеткой с плоской диагонали, существует 8 возможных направлений. Векторы ∆A и ∆B будут иметь форму, показанную в (3).
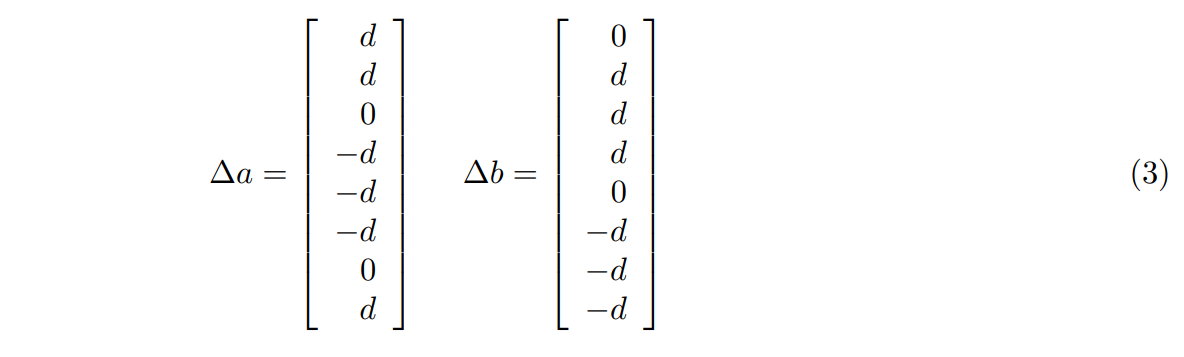
3 кодировки в штаты Кубит




3. 3.1 Кодирование структуры решетки в QUBIT STA

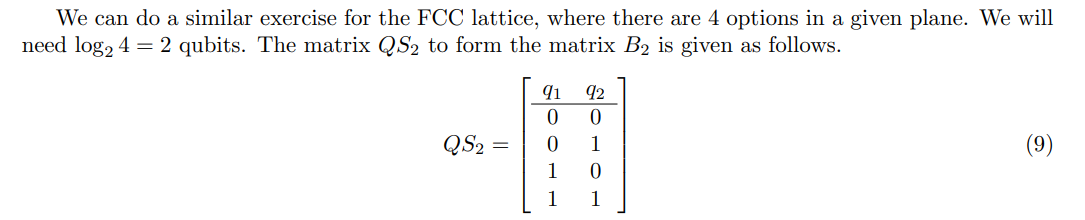
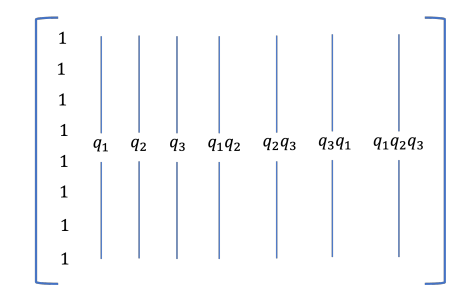
Основа B2 будет иметь форму, показанную на рис. 5. путем замены значений Q1 и Q2 в QS2 в
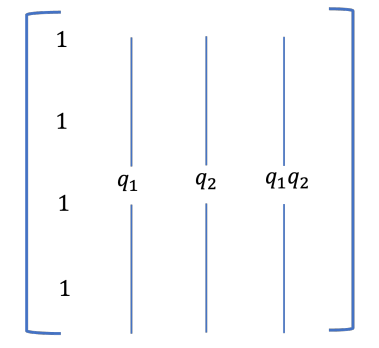
Матрица, приведенная на рис. 5, мы получим базисную матрицу B2, как указано ниже.
Как и в предыдущем случае, векторы ∆A и ∆B в (1) могут быть представлены с использованием базисных векторов в B2. Коэффициенты могут быть оценены следующим образом.

Коэффициенты, полученные для решетки FCC, следующие.
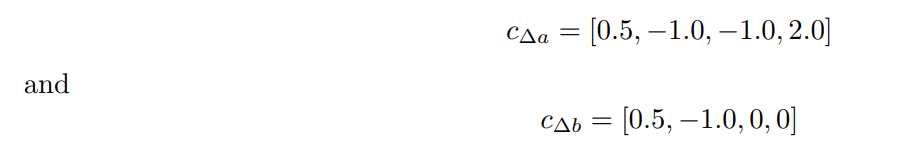
Таким образом, мы можем выразить ∆A и ∆B следующим образом.
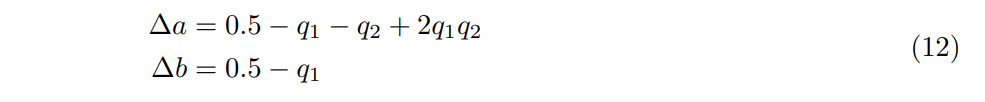
3.2 Выбор плоскости поворота
Поскольку существует 3 ортогональных плоскости (x - y, y - x и z - x), нам нужно еще два кубита больше, чтобы сделать выбор одной из плоскостей. Пусть эти два кубита будут обозначены как Q4 и Q5. Выбор может быть основан на вычислительных базисных состояниях Q4 и Q5 следующим образом.
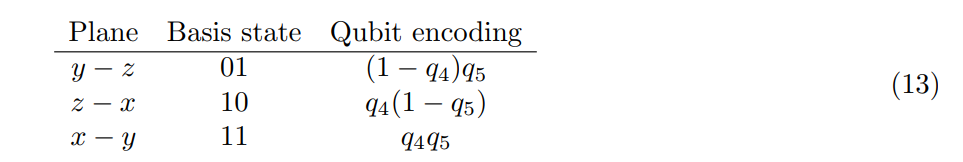
С заданными критериями отбора мы должны обновить уравнение (2) следующим образом.

3.3 Распространение его на другие структуры
Эта концепция может быть расширена и на другие структуры решетки. Нам не нужны повороты вдоль ортогональных плоскостей, таких как кубические или FCC Lateces. Самолеты могут быть под углом до рабочей плоскости. Пока каждая точка бусинки или решетки имеет равные и идентичные степени свободы, мы могли бы использовать методологию, объясненную здесь. В случае, если решетка включает в себя направления, которые всегда находятся под углом, мы могли бы покончить с кубитами, участвующими в выборе плоскости, и непосредственно перейти к указаниям кодирования в вычислительные базисные состояния. При таких обстоятельствах обновления координат после поворота будут из формы, приведенной в (15).
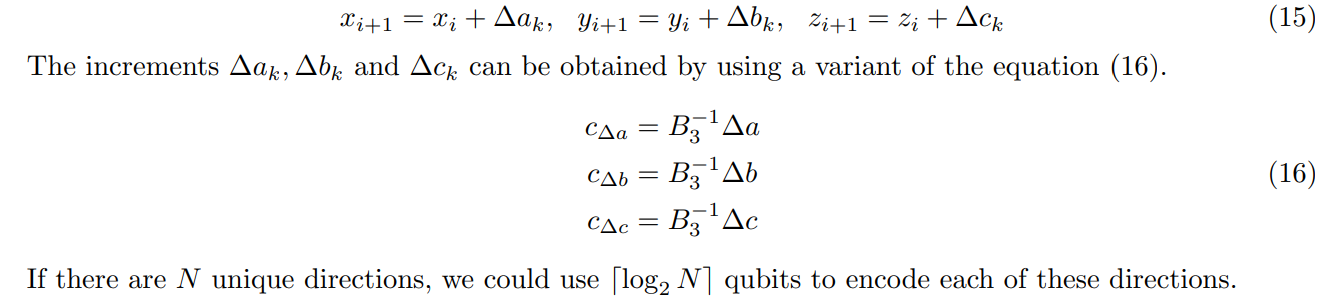
4 Выводы
В этой статье мы обсудили методологию кодирования решетки, поворачиваемые к вычислительным базисным состояниям, которые могли бы найти применение в прогнозировании структуры белка, исследовании полимерной структуры и других крупнозернистых моделях. Мы показали, как комбинация состояний кубита может быть использована для охвата пространства направлений. Эти направления могут быть вдоль самолетов, которые являются ортогональными или неорфогональными друг для друга. Мы взяли конкретные примеры кубической и FCC решетки. Тем не менее, они также могут быть распространены на другие решетки.
Ссылки
[1] В. Э. Харт и А. Ньюман, «Прогноз структуры белка с помощью решетки моделей», http: // dimacs. rutgers.edu/2aalantha/papers2/alantha-bill-bc.pdf.
[2] S. Kmiecik и Et. al., «Крупнозернистые модели белка и их применение», ACS Chem. Rev., Vol. 116, с. 7898–7936, июнь 2016 года.
[3] M. Fingerhuth, T. babej и C. Ing, «Квантовый чередовый оператор Ansatz с твердыми и мягкими ограничениями для складывания белка решетки», Arxiv Preprint Arxiv: 1810.13411, 2018.
[4] А. Пердомо, С. Трункик, И. Туберт-Броман, Г. Роуз и А. Ассуру-Гузик, «Конструкция модельных гамильтоновцев для адиабатических квантовых вычислений и его применение к поиску низкоэнергетических конформаций моделей белка решетки», Phys. Rev. A, Vol. 78, с. 012320, июль 2008.
[5] А. Роберт, П. Баркоутсос, С. Вернер и И. Тавернелли, «Ресурсный квантовой алгоритм для складывания белка», NPJ Quantum Information, vol. 7:38, 2021.
[6] J. P. Vasavi и Et. al., «Подход к решению сложной проблемы складывания белка в квантовом компьютере», Arxiv Preprint arxiv: 2311.14141v1, 2023.
Автор:
(1) Калян Дасгупта, IBM Research, Бангалор, Индия.
Эта статья есть
Оригинал

