Этот статистический тест может сэкономить 22% ваших данных (и времени)
12 августа 2025 г.Таблица ссылок
Введение
Гипотеза тестирование
2.1 Введение
2.2 Байесовская статистика
2.3 тестируйте мартингингинг
2.4 P-значения
2.5 Дополнительная остановка и взгляды
2.6 Сочетание P-значений и дополнительного продолжения
2.7 А/б -тестирование
Безопасные тесты
3.1 Введение
3.2 Классический T-критерий
3.3 Безопасный T-критерий
3.4 χ2 -Test
3,5 безопасного теста на пропорцию
Безопасное моделирование тестирования
4.1 Введение и 4.2 реализация Python
4.3 Сравнение t-теста с безопасным t-тестом
4.4 Сравнение χ2 -теста с тестом на безопасную пропорцию
Смесь последовательного теста вероятности
5.1 Последовательное тестирование
5.2 Смесь SPRT
5.3 MSPRT и безопасный T-критерий
Онлайн -контролируемые эксперименты
6.1 Безопасный t-тест на наборах данных OCE
Vinted A/B-тесты и 7.1 Safe T-критерий для Vinted A/B-тестов
7.2 безопасная пропорция для несоответствия соотношения образца
Заключение и ссылки
5.3 MSPRT и безопасный T-критерий
В этом разделе мы будем сравнивать MSPRT и безопасный T-критерий с точки зрения мощности, размера выборки и других свойств.
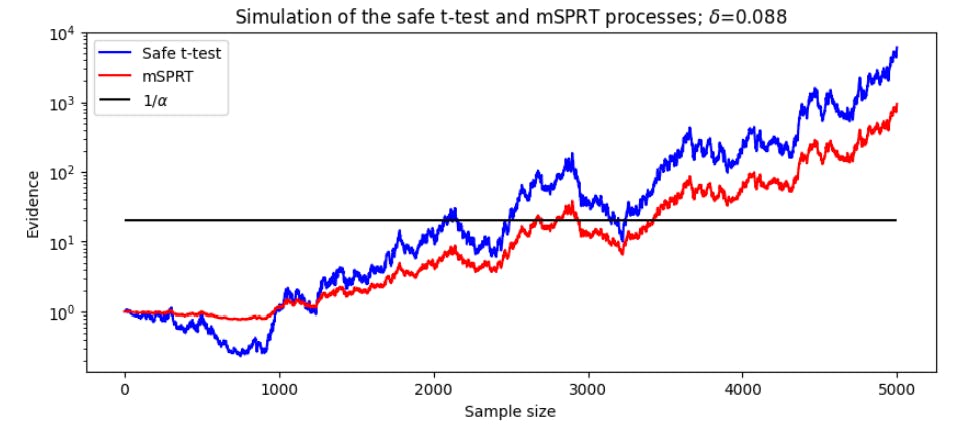
Сначала мы рассмотрим производительность статистики на паре случайных нормальных образцов со средней разницей в дисперсии Δ и единицы. Обе статистические данные ведут себя как тестирование мартингал, поэтому мы можем сравнить их визуально, когда они накапливают доказательства для и против H0. На рисунке 8 показано симуляция этих процессов.
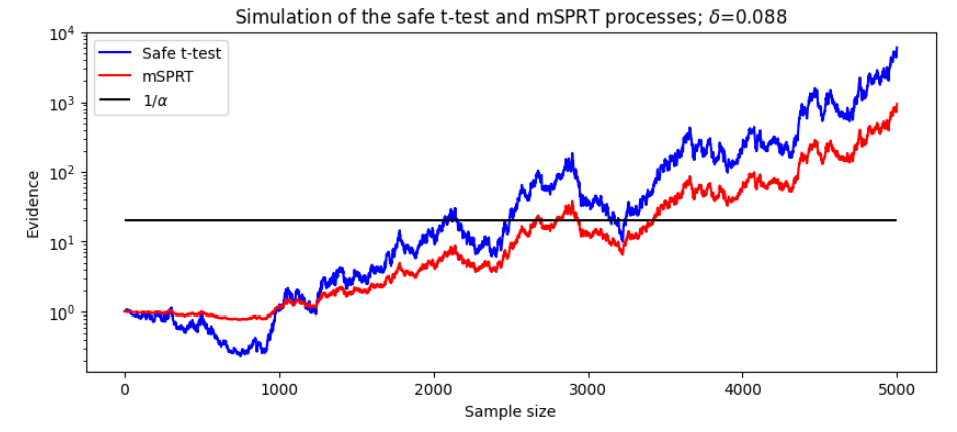
Первое, что нужно заметить, это то, что оба теста делают аналогичные выводы из данных. В первых 1000 образцов есть доказательства в пользу H0: Δ = 0, что приводит к снижению обеих тестовых статистических данных. Следующие доказательства в пользу альтернативной гипотезы H1: Δ ̸ = 0, обе статистики испытаний увеличиваются до тех пор, пока они не пересекают порог 1/α. Второе наблюдение происходит в величине, которую каждый тест весит. Поскольку доказательства первоначально подтверждают нулевую гипотезу, статистика безопасного теста уменьшается гораздо быстрее, чем статистика MSPRT. Однако по мере того, как данные, поддерживающие H1, увеличиваются, безопасная статистика превосходит статистику MSPRT, оставаясь намного выше до конца эксперимента. Последнее наблюдение происходит, когда статистика пересекает порог 1/α. В то время как безопасное тест требует менее 2100 образцов для отклонения нуля, MSPRT требуется более 2700 образцов.
С пониманием того, как безопасное t-критерий и MSPRT работают на случайной выборке, теперь мы можем рассмотреть множество моделирования с тем же размером эффекта δ. Цель этих тестов состоит в том, чтобы остановиться, когда было собрано достаточное количество доказательств против H0: Δ = 0. Поэтому мы сравним время остановки 1/α этой статистики испытаний. В тех случаях, когда эффект не обнаруживается, тест останавливается при силе 1 - β = 0,8. На рисунке 9 показан результат многих моделирования этого процесса.
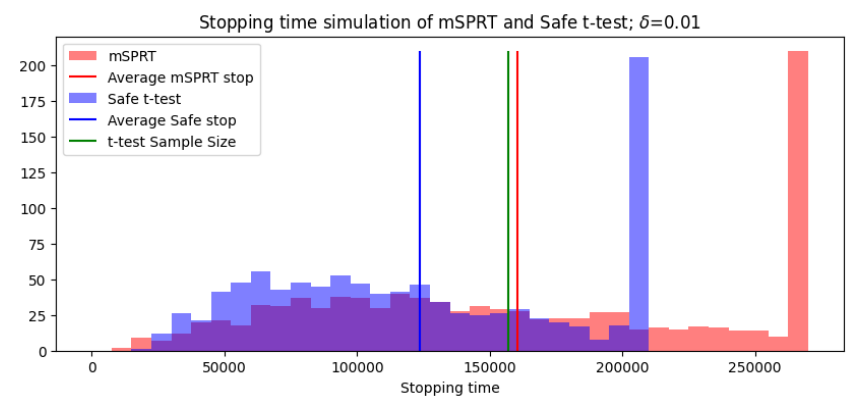
Гистограмма времени остановки на рисунке 9 показывает, что для моделируемых данных с величиной эффекта Δ = 0,01 безопасные тесты способны завершить гораздо быстрее, чем MSPRT. В среднем, Safe Test использует на 22% меньше данных, чем MSPRT. Для тестов, которые не достигают порога 1/α, тест останавливается без отвержения нулевой гипотезы. Около 20% как безопасного теста, так и MSPRT достигают этого порога, как и ожидается для теста с 80% мощностью. Эти результаты размера выборки могут быть разбиты дальше в зависимости от результата теста. Интересно узнать, например, количество образцов, необходимых в среднем, для отклонения H0. Эти результаты можно увидеть в таблице 2.
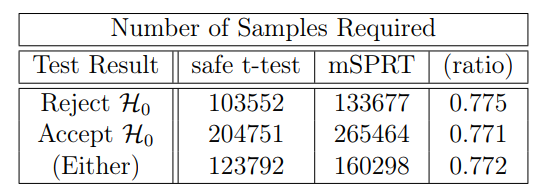
Результаты таблицы 2 имеют отношение к практикующим врачам, которые особенно обеспокоены отклонениями от нулевой гипотезы. Например, Uber использует MSPRT для мониторинга отключений своей платформы [SA23]. Учитывая, что Safe T-тест отклоняет H0 с на 22% меньше данных, это может уменьшить время для распознавания отключений и, следовательно, улучшить время отклика.
Мы видели, что для моделирования Δ = 0,01 безопасное тест завершается с использованием меньшего количества образцов, чем MSPRT, но его еще предстоит увидеть для разных величин эффекта. Следующий эксперимент проводится на 30 размерах эффектов в диапазоне от 0,01 до 0,3. Мы хотим рассмотреть два времени остановки: среднее время остановки для каждого теста и время остановки, необходимое для 80% мощности. Чтобы контекстуализировать эти результаты, мы можем рассмотреть отношение размера выборки каждого из этих тестов относительно классического теста A/B. На рисунке 10 показано среднее и максимальное время остановки безопасного t-критерия и MSPRT с точки зрения соотношения размера выборки классического t-критерия.
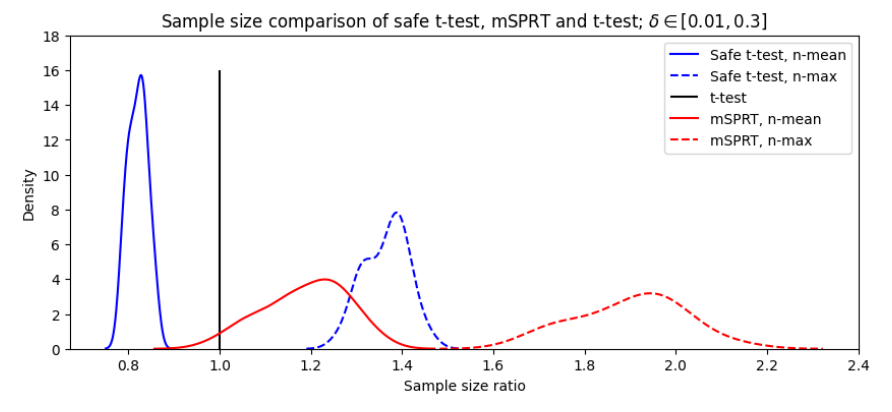
Сплошные линии на рисунке 10 представляют среднее время остановки всех моделирования для всех величин эффекта. Безопасному тесту требуется примерно на 20% меньше образцов, чем в T-тесте, в то время как MSPRT требуется примерно на 20% больше. Пунктирные линии представляют максимальные размеры выборки, необходимые для достижения 1 - β -мощности. В то время как MSPRT нуждается в примерно в два раза больше выборки, чем T-критерий для достижения этой мощности, Safe T-критерий нуждается только в примерно на 40% больше образцов.
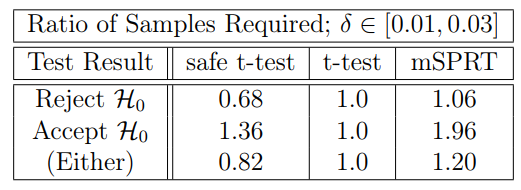
Как и в таблице 2, мы можем сравнить среднее время остановки для тестов, основанных на том, отвергают ли они или принимают H0. Эти результаты, обнаруженные в таблице 3, показывают, что для отклонения H0 Safe T-критерий использует на 32% меньше данных, чем T-критерий, в то время как MSPRT использует на 6% больше. Это дает дополнительные доказательства того, что безопасное t-критерий является более эффективным, чем MSPRT, при том, чтобы сделать выводы с теми же данными.
Чтобы сравнить среднее время остановки с функцией величины эффекта δ, мы можем снова нормализовать размеры выборки с помощью классического размер выборки T-теста. Результаты можно увидеть на рисунке 11.
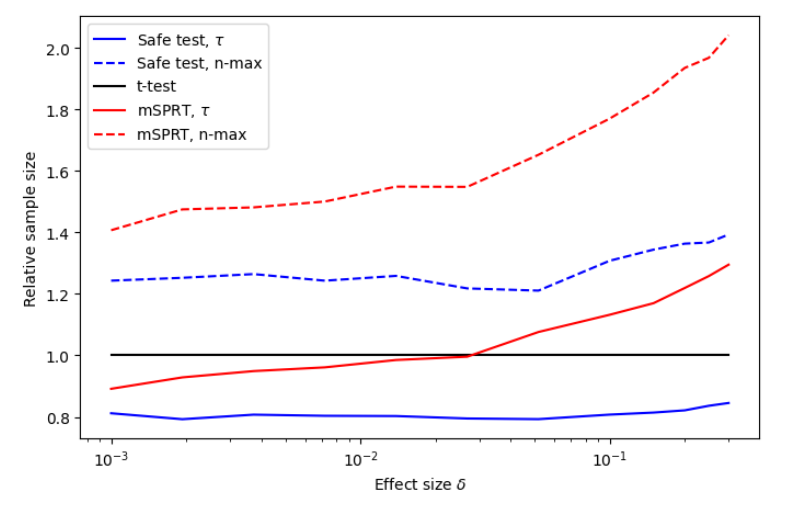
На рисунке 11 показано, что безопасные T-статистические размеры выборки меньше, чем классический t-критерий, так и MSPRT для всех δ ∈ [0,001, 0,3]. Возможность безопасного t-критерия обнаруживает эти небольшие величины эффекта, является мотиватором для его использования в онлайн-тестировании A/B.
До сих пор все моделирование проводилось с α = 0,05 и β = 0,2. Чтобы заверить читателей, что эти параметры не смещают результаты, на рисунке 12 показано время остановки при изменении этих параметров.
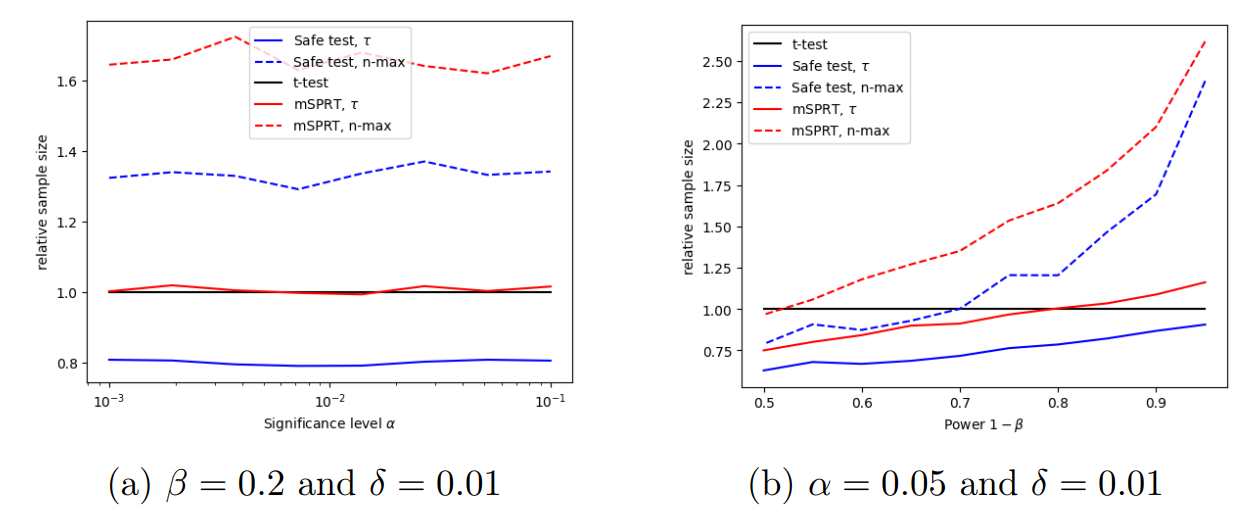
Понятно, что эффективность безопасного T-теста будет распространяться на различные сценарии тестирования, основанные на потребностях экспериментатора.
В этом разделе мы сравнили безопасное t-критерий и MSPRT с помощью различных моделирования. Было обнаружено, что безопасный T-тест останавливается раньше, чем MSPRT во всех симуляциях. Это приводит к меньшим размерам выборки и более быстрым экспериментам. Мы также обнаружили, что безопасное t-критерий способен отклонять H0 с гораздо меньшим количеством данных, чем классический T-критерий и MSPRT. В следующем разделе мы дополнительно анализируем эффективность этих статистических тестов на реальных данных A/B.
Автор:
(1) Даниэль Бизли
Эта статья есть
Оригинал

