
Двухэтапный секрет ML за Skycurtains
18 июня 2025 г.Таблица ссылок
Аннотация и 1. Введение
2. Набор данных
3. Метод Skycurtains и 3.1 Countainsf4f
3.2. Обнаружение линии
4. Результаты
4.1. Метрики
4.2. Полное сканирование потока GD-1
5. Заключение, подтверждение, доступность данных и ссылки
Приложение A: Drainainsf4f обучение и сведения о настройке гиперпараметра
А1. Countainsf4f имеет предварительную обработку
A2 Настройка гиперпараметра
3 метод Skycurtains
Skycurtains - это двухэтапный подход, чтобы найти звездные потоки в модельном агностическом манере. Первый этап - шторы, за которым следует шаг CWOLA. Этот этап используется для вывода порога для выбора звезд кандидата для второго этапа. Первый этап флага всех чрезмерных аномальных. Но поскольку мы ищем звездные потоки, нам нужно идентифицировать линейные структуры в популяции звезд кандидатов. Это делается вторым этапом метода Skycurtains, который использует преобразование Hough (Hough 1962) для обнаружения линий. Детали обучения и реализации двух этапов обсуждаются в следующих разделах.
3.1 Curtainsf4f
Countainsf4f создает обогащенный фоном шаблон в области сигнала, изучая условное преобразование функций от боковых полос в область сигнала, в зависимости от правильного движения. Curtainsf4f использует максимальную потерю вероятности транспортируемых данных и целевые данные, использующие метод потоков для потоков, введенный в Golling et al. (2023) Чтобы узнать эту трансформацию.
Нормализующий поток (Papamakarios et al. 2021) - это модель, которая изучает вариант преобразования 𝑓𝜙: 𝑧 → 𝑥 между основным распределением до целевого распределения по максимальной вероятности, где 𝑧 ∼ 𝜃 𝜃 и 𝑥 ∼ 𝑃𝑋. Обычным выбором для базового распределения является стандартное нормальное распределение. Функция потерь для обучения этого нормализующего потока 𝑓𝜙 определяется изменением формулы переменных
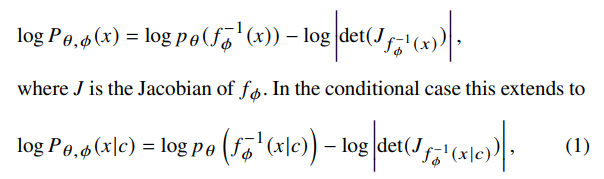
где 𝑐 являются условными свойствами, и 𝜙 являются обучаемыми параметрами нормализующего потока 𝑓, а 𝜃 являются параметрами базового распределения.
В методах обнаружения аномалий, таких как (Nachman & Shih 2020), кто-то изучает распределение 𝑝𝜙 (𝑥 | 𝑐) для 𝑐 в боковых областях, а затем запрашивает условный нормализующий поток для 𝑐 в области сигнала, чтобы получить модель, управляемую данными для фонового шаблона. Эта «автоматическая» интерполяция условной плотности проста и эффективна, как бы эмпирически она была обнаружена в (Nachman & Shih 2020), что для точной интерполяции в боковую полосу, необходимую для обучения 𝑝𝜙 (𝑥 | 𝑐) во всем дополнении области сигнала. Для поиска скользящего окна, вычислительно дорого обучать отдельный поток на дополнение каждой области сигнала. Curtainsf4f улучшает эту ситуацию, обучая второй условный поток, чтобы изучить преобразование между данными левой и правой полосы. Этот поток, как обнаружено, находится гораздо лучше, поскольку преобразования, которые необходимо изучить, намного проще, и эта простота действует как неявная регуляризация при интерполяции в область сигнала. Можно получить точный фоновый шаблон в области сигнала с просто обучением на более узких боковых полосах вместо всего комплемента области сигнала. Процедура CORTANESF4F также позволяет обучать один базовый поток для изучения 𝑝𝜙 (𝑥 | 𝑐) для всех данных, а затем отбираться из этого в узких боковых полосах, которые можно обучить верхний поток для интерполяции в любую область сигнала. Таким образом, дорогостоящий этап обучения базовому потоку должен быть сделан только один раз, а затем дешевый этап обучения верхнего потока может быть повторен с гораздо меньшими вычислительными затратами.

Surtainsf4f обучается в обоих направлениях. Правный проход преобразует данные от низких до более высоких значений целевых целевых движений, тогда как данные обратного прохода преобразуют данные из высоких до низких целевых значений. Данные взяты из как SBS, так и целевые правильные значения движения случайным образом присваиваются каждой точке данных, используя все правильные значения движения в партии. Данные передаются через сеть в прямом или обратном проходе, в зависимости от того, является ли правильное движение больше или меньше, чем их первоначальное правильное движение. Сеть обусловлена функцией начального и целевого правильного движения, причем два значения упорядочены в порядке возрастания. Эта функция может быть, например, разница между двумя или просто оба значения, объединенные. Срок вероятности оценивается с использованием одного базового распределения, обученного данным SB1 и SB2. Потеря для партии рассчитывается из среднего значения вероятностей, рассчитанных по прямым и обратным проходам. Схематический обзор показан на рисунке 3.
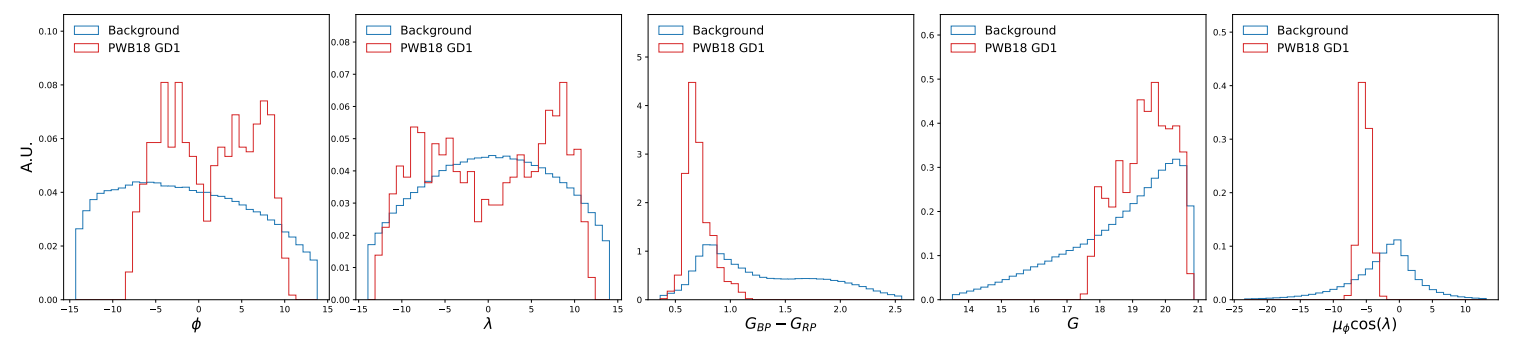
Базовый поток обучается на боковых данных со стандартным нормальным распределением в качестве целевого предыдущего. Это обусловлено правильным движением. Верхний поток обучается между данными, взятыми из боковых полос. Преобразование обусловлено конкатенированным кортежом начального и целевого правильного движения. В зависимости от того, какое правильное движение выбирается в качестве функции кондиционирования, нижняя задача поиска потока может быть затронута. Это связано с тем, что звезды кандидатов в потоку могут иметь нетривиальную корреляцию и, следовательно, могут производить по плотности различных форм в двух правильных движениях соответственно. В этой работе мы используем 𝜇𝜆 в качестве условной функции. Остальные особенности, то есть [𝜙, 𝜆, 𝐺, 𝐺BP - 𝐺RP, 𝜇𝜙 COS 𝜆] используются для характеристики шаблона.
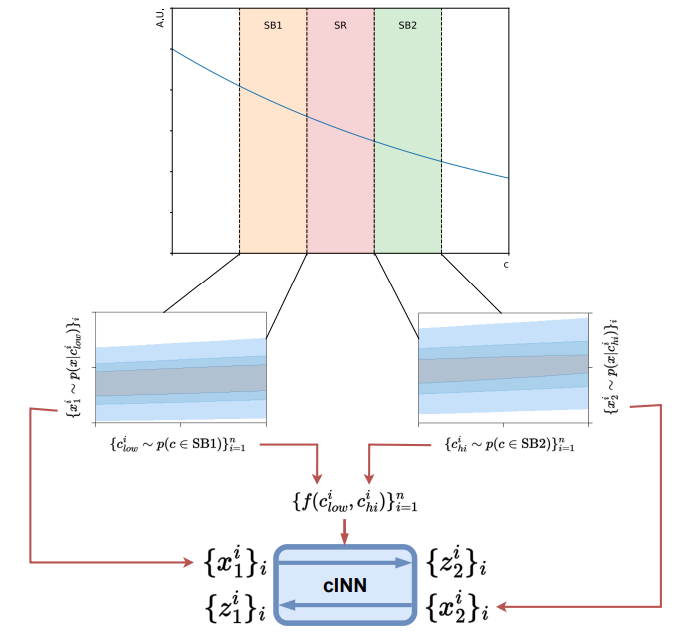
Одним из важных аспектов метода штор -штарей является определение регионов сигнала и боковой полосы. На рисунке 4 мы показываем распределение 𝜇𝜆 фоновых звезд и звезд GD-1 в боковых полосах (SB1, SB2) и области сигнала (SR). В отличие от метода Via Machinae, где область боковой полосы была комплементарной областью выбранного SR, Skycurtains определяет область боковой полосы, как правило, 2-6 Mas/год. Поскольку верхний поток должен только изучать небольшое (но не обязательно тривиальное) преобразование данных боковых полос для создания шаблона в SR, мы обнаруживаем эту ширину боковой полосы. Это также сокращает общее время обучения по сравнению с Via Machinae, поскольку, несмотря на то, что оба метода, состоящие из двух генеративных моделей, вторая генеративная модель Skycurtaines эффективно учится на более узких боковых полосах. Чтобы продемонстрировать эффективность метода на потоке GD-1, мы определяем область сигнала как интервал, в котором содержится сигнал. В фактическом анализе, где местоположение сигнала не известно априори, нужно было бы сканировать несколько значений 𝜇𝜆 с помощью метода штурмановф4F. Здесь вступает в игру модульность метода CORTANESF4F, так как базовый поток может быть обучен на весь участок неба и заморожен. После этого верхние потоки могут быть обучены на отдельных областях, представляющих интерес. Это значительно снижает вычислительную стоимость обучения модели, позволяя обучению базового потока один раз и повторно используется для нескольких интересующих регионов.
После обучения модели Counainsf4f, обогащенный фоном шаблон построен путем преобразования данных из боковых полос в область сигнала, обусловленную на корте начального и правильного движения цели. Правильные движения цели в области сигнала отображаются из подгонки плотности ядра при правильном распределении движения. Мы тренируем ансамбль из 10 многослойных классификаторов на основе персептрона [1]

Между этим шаблоном и данными области сигнала. Затем оценки агрегируются путем получения среднего балла и используются для классификации данных в области сигнала. Лучшие 0,1% большинство сигнальных звезд выбираются в качестве кандидатов на следующий шаг. Этот порог выбирается для удаления наибольшего фона, таких как звезды из области сигнала, который является настраиваемым параметром и может быть скорректирован на основе желаемой чистоты и эффективности сигнала.
3.2 Обнаружение линии
Шаг Shutainsf4f дает нам набор звезд, которые производят чрезмерную плотность в пространстве объектов. Нам все еще нужно отфильтровать избыточность, которая особенно похожа на линию, так как мы заинтересованы в звездных потоках. Мы используем хорошо известный алгоритм поиска линии для оценки параметров линии потока через преобразование Хаф, как это было сделано (Shih et al. 2021, 2023). Поскольку мы не применяем фидуциальный разрез, чтобы устранить звезды за пределами радиуса 10 °, мы можем использовать полный набор звезд, которые пропускают шторфы, вырезанные в патче, чтобы оценить параметры линии.
Для данной звезды, расположенной в (𝜙 ′, 𝜆 ′), преобразование Hough-это отображение от пространства 𝜙-𝜆 в пространство параметров 𝜌-𝜃, определяемое как:

Авторы:
(1) Debajyoti Sengupta, Département de Physique Nucléaire et Corpusculaire, Женевский университет, Швейцария (debajyoti.sengupta@unige.ch);
(2) Стивен Маллиган, департамент De Physique Nucléaire et Corpusculaire, Женевский университет, Швейцария;
(3) Дэвид Ши, NHETC, Департамент физики и астрономии, Рутгерс, Пискатауэй, Нью -Джерси 08854, США;
(4) Джон Эндрю Рейн, Département de Physique Nucléaire et Corpusculaire, Женевский университет, Швейцария;
(5) Тобиас Голлинг, Département de Physique Nucléaire et Corpusculaire, Женевский университет, Швейцария.
Эта статья есть
[1] Подробности об архитектуре можно найти в Приложении A
Оригинал

