
Тайваньское исследование картирует глобальный разрыв в исследованиях в выборе аудита на основе искусственного интеллекта
13 июня 2025 г.Авторы:
(1) Гуан-и-Йи Шеу, Департамент инновационных приложений и управления/бухгалтерского учета и информационной системы, Чанг-Юнг Христианский университет, Тайнан, Тайвань и этот автор внесли одинаковый вклад в эту работу (xsheu@hotmail.com);
(2) Наи-ру-Лю, факультет бухгалтерского и информационной системы, Христианский университет Чанг-Юнг, Тайнан, Тайвань (110B17727@mailst.cjcu.edu.tw).
Примечание редактора: это часть 2 из 3 исследований, в котором изучается, как выборка с AI может помочь аудиторам обрабатывать большие наборы данных. Прочитайте остальное ниже.
Таблица ссылок
- Аннотация и 1. Введение
- 2. Обзор литературы
- Наивный байесовский классификатор
- 4. Результаты
- Дискуссия
- Выводы и ссылки
2. Обзор литературы
Как указывалось ранее, только в некоторых исследованиях были отобраны данные с использованием алгоритма машинного обучения при аудитории. Эта разреженность приводит к преследованию в поисках совета по реализации этого исследования.
Если цель состоит в том, чтобы повысить эффективность аудита, некоторые опубликованные исследования (например, [5])) интегрированное машинное обучение с отбором выборки для обнаружения аномалий. Например, Chen et al. [5] выбрали алгоритмы ID3, CART и C4.5, чтобы найти аномалии в финансовых операциях. Их результаты показали, что алгоритм машинного обучения может упростить аудит финансовых транзакций, эффективно изучая их атрибуты.
Schreyer et al. [8,9] построили нейронную сеть AutoEncoder для образцов записей журнала в своих двух документах. Они кормили атрибуты этих записей в журнале в полученный автоэкодер. Однако Schreyer et al. Нанесенные рисунки для описания представителей образцов.
Ли [10] построил еще одну нейронную сеть AutoEncoder для выборки налогоплательщиков. В отличие от Schreyer et al. [8,9], Ли рассчитал ошибку реконструкции для количественной оценки репрезентативности образцов. Этот показатель измеряет разницу между входными данными и выходами, реконструированными с использованием образцов. Более низкие ошибки реконструкции указывают на лучшую репрезентативность оригинальных налогоплательщиков. Кроме того, Ли [10] использовал алгоритм априора, чтобы найти тех налогоплательщиков, которые могут быть ценными для пробеги вместе. Если один налогоплательщик нарушает некоторые законы, другие налогоплательщики также могут быть мошенническими.
Chen et al. [11] применили случайный классификатор леса, алгоритм XGBOOST, квадратичный дискриминантный анализ и модель поддержки векторных машин для образцов атрибутов биткойнов ежедневных данных транзакций. Эти атрибуты содержат цены на недвижимость и сеть, торговлю и рынок, внимание и золотые спотовые цены. Цель этого предыдущего исследования - предсказать ежедневные цены биткойнов. Chen et al. [11] обнаружили, что алгоритмы машинного обучения предсказывают более точно 5-минутные цены на биткойн, чем статистические методы.
В отличие от вышеупомянутых четырех исследований, Чжан и Трубей [3] разработали методы подборочки и перепродажи, чтобы выделить редкие события в проблеме отмывания денег. Их целью было улучшение производительности алгоритмов машинного обучения в моделировании событий отмывания денег. Чжан и Трубей [3] приняли байесовскую логистическую регрессию, дерево решений, классификатор случайного леса, модель поддержки векторных машин и искусственную нейронную сеть.
В полях, отличных от аудита, перечислены три примера: Liberty et al. [12] определили специализированную проблему регрессии для расчета вероятности отбора каждую запись набора данных об просмотре. Цель состояла в том, чтобы попробовать небольшой набор записей, по которым оценка агрегатных запросов может быть выполнена как эффективно, так и точно. В результате их решения проблемы регрессии используется простой алгоритм управляемого эмпирического минимизации риска. Liberty et al. [12] пришли к выводу, что интеграция машинного обучения улучшила как однородные, так и стандартные методы стратифицированной выборки.
Hollingsworth et al. [13] Полученные модели генеративного машинного обучения для повышения эффективности вычислений в выборке высоких параметров. Их результаты достигают порядка повышения эффективности отбора проб по сравнению с поиском BruteForce.
Artrith et al. [14] объединили генетический алгоритм и специализированный потенциал машинного обучения, основанный на искусственных нейронных сетях, чтобы ускорить выборку аморфных и беспорядочных материалов. Они обнаружили, что интеграция машинного обучения уменьшила необходимые расчеты в выборке.
В других соответствующих исследованиях обсуждались преимущества или проблемы интеграции алгоритма машинного обучения с аудитом данных. Эти исследования только поощряют или напоминают текущему исследованию, чтобы заметить эти преимущества или проблемы. Например, Huang et al. [15] предположил, что алгоритм машинного обучения может служить «черным ящиком», чтобы помочь аудитору. Тем не менее, аудиторам может понадобиться помощь в освоении алгоритма машинного обучения. Кроме того, аудиторы могут иметь неправильное понимание производительности алгоритма машинного обучения. Это недоразумение заставляет аудиторов полагать, что мы всегда можем получить точную классификацию или кластеризацию данных, используя алгоритм машинного обучения. Кроме того, это повышает эффективность и эффективность экономии, анализирует массовые наборы данных и сокращает время, затрачиваемое на задачи. Поэтому мы должны обеспечить, чтобы производительность алгоритма машинного обучения была достаточно хорошей, прежде чем применять его для помощи аудиторам.
3. Наивный классификатор Байеса


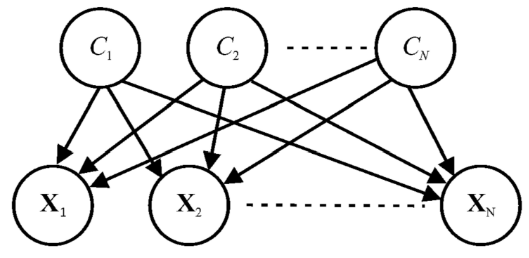
Относительно традиционных методов выборки [7], в этом исследовании разрабатывает пользовательские и основанные на элементах подходы в интеграции уравнений (3)-(4) с выбором аудиторских доказательств:
я. Подход на основе пользователя: в попытке генерировать беспристрастные представления данных, классификация (x1, c1), (x2, c2). Полем Полем , (XN, CN) и вычислите два процентиля симметричных вокруг медианы каждого класса в соответствии с профессиональными предпочтениями аудитора. Нарисуйте X1, x2 ,. Полем Полем Xn ограничен полученными процентилями в качестве аудиторских доказательств, и
II Подход на основе элементов: Предположим, XJ, CJ (1 ≤ J ≤ N) представляют рискованные образцы. Асимметрически выберите их на основе значений pr ci | xj (1 ≤ i ≤ n) в качестве аудиторских доказательств после классификации (x1, c1), (x2, c2). Полем Полем , (Xn, cn:.
3.1. Пользовательский подход

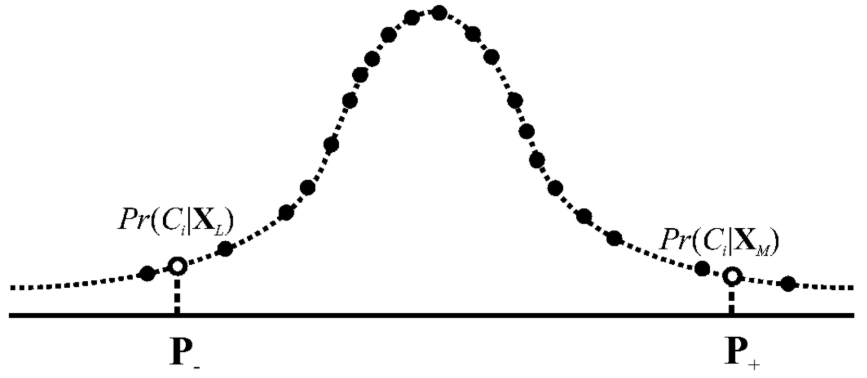

Что касается существующих методов выборки аудита [4], настоящий пользовательский подход может быть идентичен комбинации методов монетарной и переменной выборки.
3.2. Подход на основе элементов

Дальнейшее упрощение уравнения (10) приводит к

Что касается существующих методов выборки аудита [4], настоящий подход, основанный на элементах, может быть эквивалентен комбинации нестатистических и монетарных методов выборки.
Как и раздел 3.1, мы рассчитываем индекс репрезентативности RI [3], чтобы проверить, являются ли аудиторские доказательства достаточно репрезентативными.
3.3. Гибридный подход
Аудиторы могут гибридизировать полученные работы в разделах 3.1-3.2, чтобы сбалансировать репрезентативность и рискованность. Сначала мы применяем пользовательский подход к образцам репрезентативных членов, ограниченных двумя процентилями, симметричными вокруг медианы класса CI (1 ≤ I ≤ N). Применение основанного на элементах подход к образцам асимметрично рискованных образцов в следующий раз выполняется среди полученных результирующих образцов.
Эта статья естьДоступно на ArxivПод атрибуцией-некоммерческими показателями 4.0 Международная лицензия.
Оригинал

