Защита скидок от майнеровских игр с R-TFRM

Защита скидок от майнеровских игр с R-TFRM

30 июня 2025 г.

Аннотация и 1. Введение

  1. Связанная работа

  2. Предварительные

    3.1 TFMS: желательные свойства

    3.2 Механизм перераспределения Groves (RM)

  3. Идеал-TFRM: невозможность достижения строго положительного индекса перераспределения

  4. Механизм перераспределения платы за транзакцию (TFRM)

  5. R-TFRM: TFRM, надежный для манипуляций с шахтером

    6.1 R-TFRM: анализ влияния манипуляций с шахтером на скидку и доходы от шахтеров

  6. R2-TFRM: надежный и рациональный TFRM

  7. Заключение и ссылки

A. Доказательства для результатов раздела 4 и 5

B. Доказательства для результатов раздела 6

C. Доказательства для результатов раздела 7

6 R-TFRM: TFRM, устойчивый к манипуляциям с майнером

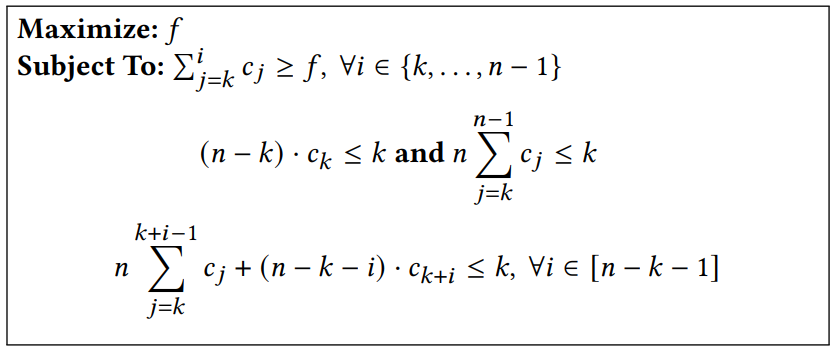
Figure 4: R-TFRM: Linear Program Independent of the bid vector b

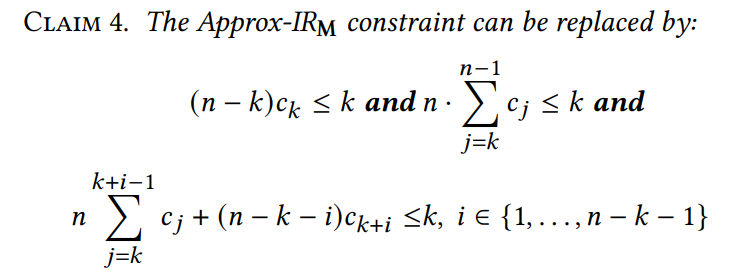
Используя претензии 3 и 4, мы переформулируем линейную программу на рисунке 3, чтобы она не зависела от векторов BID. На рисунке 4 представлен этот переформулированный LP.

Оптимальная фракция перераспределения наихудшего случая.Затем мы предоставляем аналитическое решение линейной программы на рисунке 4 и, таким образом, также указываем оптимальный перераспределенные фракции.

6.1 R-TFRM: анализ влияния манипуляций с шахтером на скидку и доходы от шахтеров

Из теоремы 4 и теоремы 5 мы видим, что в R-TFRM часть платежей перераспределена для пользователей Top-K, то есть, 𝑘/𝑛, одинакова для честного и стратегического майнера. Это подразумевает, что R-TFRM устойчив к манипуляциям с шахтером, одновременно является оптимальным.

Авторы:

(1) Sankarshan Damle, IIIT, Хайдарабад, Хайдербад, Индия (Sankarshan.damle@research.iiit.ac.in);

(2) Маниша Падала, IISC, Бангалор, Бангалор, Индия (manishap@iisc.ac.in);

(3) Суджит Гуджар, IIIT, Хайдарабад, Хайдербад, Индия (sujit.gujar@iiit.ac.in).

Эта статья естьДоступно на ArxivПод CC по лицензии 4.0.

Оригинал

🔥 Популярное на этой неделе

⭐ Самое популярное

Categories


PREVIOUS ARTICLE
NEXT ARTICLE