Освоение теста последовательного отношения с последовательным соотношением смеси (MSPRT) для A/B -тестирования
tech-stories data-driven-decision-making safe-ab-testing real-time-ab-testing avi-statistical-methods msprt-comparison hypothesis-testing p-hacking hypothesis-testing-methods

Освоение теста последовательного отношения с последовательным соотношением смеси (MSPRT) для A/B -тестирования

12 августа 2025 г.

  1. Введение

  2. Гипотеза тестирование

    2.1 Введение

    2.2 Байесовская статистика

    2.3 тестируйте мартингингинг

    2.4 P-значения

    2.5 Дополнительная остановка и взгляды

    2.6 Сочетание P-значений и дополнительного продолжения

    2.7 А/б -тестирование

  3. Безопасные тесты

    3.1 Введение

    3.2 Классический T-критерий

    3.3 Безопасный T-критерий

    3.4 χ2 -Test

    3,5 безопасного теста на пропорцию

  4. Безопасное моделирование тестирования

    4.1 Введение и 4.2 реализация Python

    4.3 Сравнение t-теста с безопасным t-тестом

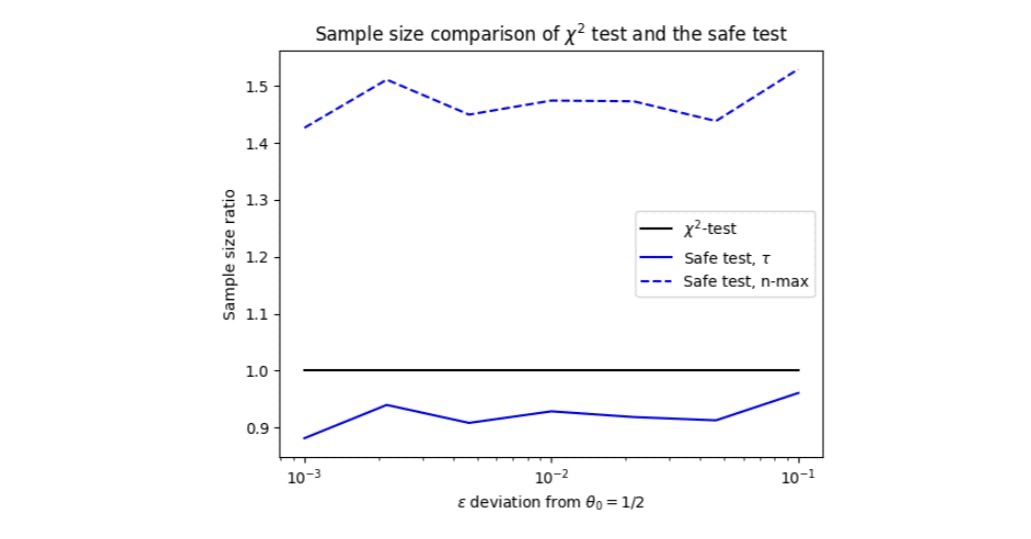
    4.4 Сравнение χ2 -теста с тестом на безопасную пропорцию

  5. Смесь последовательного теста вероятности

    5.1 Последовательное тестирование

    5.2 Смесь SPRT

    5.3 MSPRT и безопасный T-критерий

  6. Онлайн -контролируемые эксперименты

    6.1 Безопасный t-тест на наборах данных OCE

  7. Vinted A/B-тесты и 7.1 Safe T-критерий для Vinted A/B-тестов

    7.2 безопасная пропорция для несоответствия соотношения образца

  8. Заключение и ссылки

5 Проверка последовательного соотношения смеси

5.1 Последовательное тестирование

Поскольку сложная инфраструктура A/B -тестирования размножалась, также имеют возможность взглянуть на результаты испытаний [Joh+17]. Как мы уже видели, это приводит к непреднамеренному следствию раздувания ложной положительной скорости. Чтобы воспользоваться своей инфраструктурой, крупные технологические компании начали реализовывать статистические методы, которые действительны в любое время. Эта область статистики известна как последовательное тестирование или вывод для в любом случае. Последовательное тестирование произошло с оригинальной статьей Уолда на субъекту, последовательные тесты статистических гипотез [WAL45]. Уолд вводит первый метод последовательного тестирования, известный как тест по сравнению с последовательным соотношением вероятности (SPRT). SPRT представляет собой тест размера M с одной выборкой, который делит пространство выборки на три взаимоисключающих областях, соответствующих принятию решения: либо принимайте H0, отклоните H0 или продолжайте выборку. Количество для определения решения - это апостериорная вероятность данных при H1, разделенной на заднюю вероятность при H0, P (D | H1)/P (D | H0). Это хорошо известный фактор байеса между альтернативными и нулевыми гипотезами и тесно связан с e-variables в безопасном тестировании [GHK23].

Wald и Wolfowitz доказали, что SPRT является оптимальным последовательным тестом с точки зрения статистической мощности [WW48]. Следует отметить, однако, что их формулировка последовательного теста не совпадает с составлением безопасных тестов. Их доказательство основано на разделении пространства коэффициента вероятности на три региона: принять H0, отклонить H0 или продолжить выборку. И наоборот, безопасное t-критерий является оптимальным с точки зрения выращивания [Pér+22], что означает, что E-переменная E будет расти быстрее всего, когда H0 не правда. Решение об отклонении H0 принимается при e ≥ 1/α, в то время как противоположное решение о принятии H0 может быть принято в любое время. Понять различные формулировки этих последовательных тестов, и их доказательства их оптимальности должны помочь усвоить относительные характеристики двух тестов.

5.2 Смесь SPRT

Разработка теста A/B для последовательного тестирования включала расширение SPRT для функционирования с помощью данных с двумя выборками. Это было достигнуто Johari et al. [Joh+17] Кто впервые подготовил метод A/B -тестирования, известный как тест последовательного соотношения смеси (MSPRT). Этот тест был принят в крупных технологических компаниях, таких как Uber и Netflix [SA23]. Как и в случае с безопасным t-тестом, MSPRT оптимально работает с гранулированными последовательными данными. MSPRT по существу похож на SPRT, с предварительным убеждением, что истинный параметр находится близко к θ0. Давайте рассмотрим математические детали этого теста более подробно.

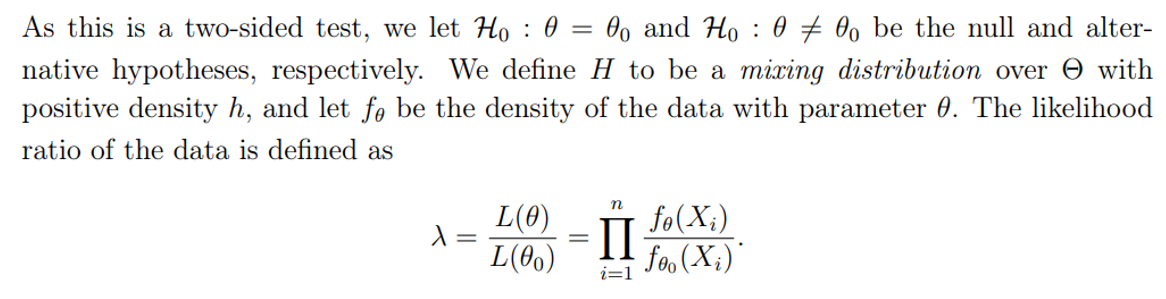
Мы сохраним статистику MSPRT в его форме мартингейла, чтобы сравнить производительность с безопасным t-тестом.

Автор:

(1) Даниэль Бизли

Эта статья естьДоступно на ArxivПод атрибуцией-некоммерческими показателями 4.0 Международная лицензия.

Оригинал

Recent Post

Categories

PREVIOUS ARTICLE
NEXT ARTICLE