
Свойства функции logsumexp: леммы для энергетических функций
24 июня 2025 г.Таблица ссылок
Аннотация и 1 введение
2 Связанная работа
3 модели и 3.1 ассоциативные воспоминания
3.2 трансформаторные блоки
4 Новая энергетическая функция
4.1 Слоистая структура
5 Потеря по перекрестной энтропии
6 Эмпирические результаты и 6.1 Эмпирическая оценка радиуса
6.2 Обучение GPT-2
6.3 Тренировка ванильных трансформаторов
7 Заключение и подтверждение
Приложение A. отложенные таблицы
Приложение B. Некоторые свойства энергетических функций
Приложение C. отложенные доказательства из раздела 5
Приложение D. Трансформатор Подробности: Использование GPT-2 в качестве примера
Ссылки
Приложение B. Некоторые свойства энергетических функций
Мы вводим некоторые полезные свойства функции logsumexp, определенной ниже. Это особенно полезно, потому что функция SoftMax, широко используемая в моделях трансформатора, является градиентом функции logsumexp. Как показано в (Grathwohl et al., 2019), logsumexp соответствует энергетической функции классификатора A.
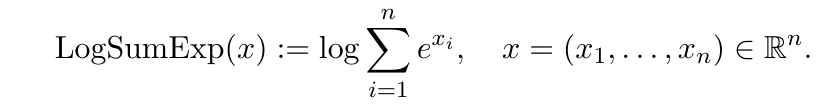
Лемма 1Logsumexp (x)это выпуклый.
Доказательство
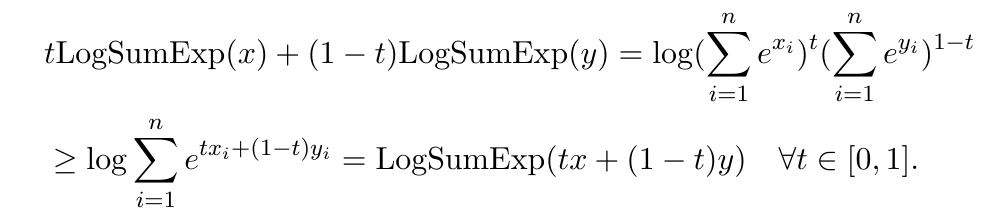
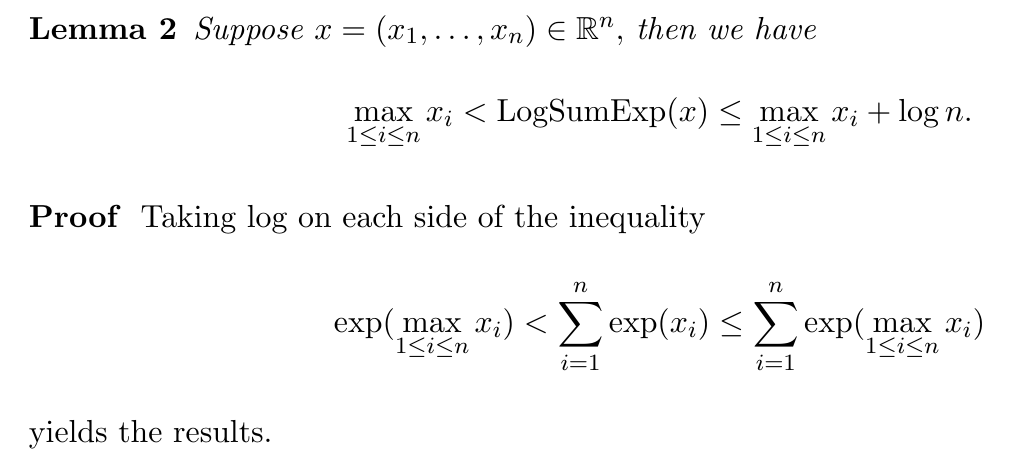
Следовательно, у нас есть следующее плавное приближение для функции MIN.

B.1 Доказательство предложения 2
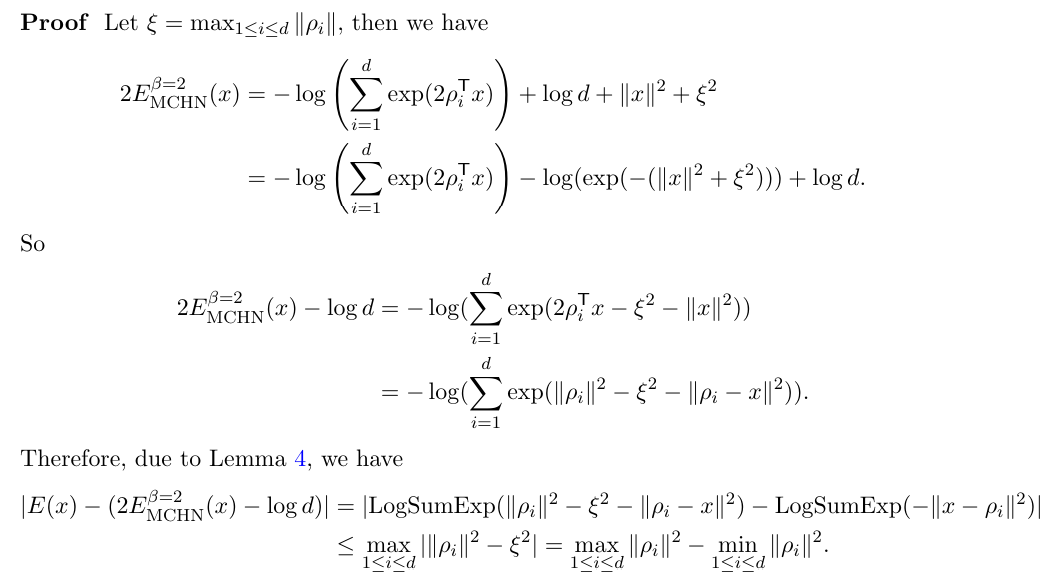
Авторы:
(1) Xueyan Niu, Theory Laboratory, Central Research Institute, 2012 Laboratories, Huawei Technologies Co., Ltd.;
(2) Бо Бай Байбо (8@huawei.com);
(3) Lei Deng (deng.lei2@huawei.com);
(4) Вэй Хан (harvey.hanwei@huawei.com).
Эта статья есть
Оригинал

