Как безопасные тесты уменьшают размеры выборки без ущерба для статистической достоверности
12 августа 2025 г.Таблица ссылок
Введение
Гипотеза тестирование
2.1 Введение
2.2 Байесовская статистика
2.3 тестируйте мартингингинг
2.4 P-значения
2.5 Дополнительная остановка и взгляды
2.6 Сочетание P-значений и дополнительного продолжения
2.7 А/б -тестирование
Безопасные тесты
3.1 Введение
3.2 Классический T-критерий
3.3 Безопасный T-критерий
3.4 χ2 -Test
3,5 безопасного теста на пропорцию
Безопасное моделирование тестирования
4.1 Введение и 4.2 реализация Python
4.3 Сравнение t-теста с безопасным t-тестом
4.4 Сравнение χ2 -теста с тестом на безопасную пропорцию
Смесь последовательного теста вероятности
5.1 Последовательное тестирование
5.2 Смесь SPRT
5.3 MSPRT и безопасный T-критерий
Онлайн -контролируемые эксперименты
6.1 Безопасный t-тест на наборах данных OCE
Vinted A/B-тесты и 7.1 Safe T-критерий для Vinted A/B-тестов
7.2 безопасная пропорция для несоответствия соотношения образца
Заключение и ссылки
4 моделирования безопасного тестирования
4.1 Введение
В этом разделе мы сравниваем классический t-критерий с безопасным t-критерием и тест χ2 с тестом на безопасную пропорцию. Тщательная библиотека для безопасного тестирования была разработана в R [LTT20]. С целью увеличения принятия в области науки о данных мы перенесли код для безопасного t-критерия и безопасного теста на пропорцию в Python.
4.2 Реализация Python
В то время как логика безопасного t-критерия остается прежней, в исходном коде был ряд неэффективности, которые необходимо решить, чтобы работать с большими размерами выборки. Улучшения подробно описаны здесь.
Первое улучшение происходит при определении размера выборки, необходимого для партийного процесса данных. Исходная функция выполняет линейный поиск от 1 до произвольного большого количества. Для каждого возможного размера выборки в диапазоне функция вычисляет E-значение на основе размеров выборки, степеней свободы и величины эффекта. Цикл разрывается, когда E-значение больше 1/α. Поскольку это монотонно увеличивающаяся функция, бинарный поиск значительно увеличивает расчет, снижая вычислительную сложность от O (n) до O (log n). Эта оптимизация оказалась необходимой при работе с миллионами образцов.
Необходимым улучшением скорости является расчет времени остановки для силы 1 - β. Это определяется путем моделирования данных, различающихся в результате минимального размера эффекта. В ходе n моделирования данные длины М индивидуально транслируются, чтобы определить точку, в которой E-значение пересекает 1/α. Еще раз, этот процесс осуществляется с помощью линейного поиска. Чтобы оптимизировать эту функцию, расчет мартингейла параллелизируется по всему вектору длины m. Вычислительная сложность остается O (NM), но векторное вычисление происходит в коде Numpy, в отличие от петли Python. Код Numpy написан в C, следовательно, расчет намного быстрее.
Окончательная модификация заключается не в снижении вычислительной сложности, а в улучшении возможностей теста на безопасную пропорцию. Этот тест был записан в R в качестве теста с двумя выборками с фиксированными размерами партии. Для нашего варианта использования тест с одной выборкой с переменными размерами партии был необходим для определения коэффициента несоответствия выборки и, следовательно, был разработан для пакета Python.
4.3 Сравнение t-теста с безопасным t-тестом
Самый простой способ понять безопасное t-критерий-это сравнить его с классической альтернативой. Мы выполняем моделирование величины эффекта Δ и нулевой гипотезы H0: Δ = 0. Установка уровня значимости α = 0,05 Мы можем моделировать величину эффекта δ между двумя группами, чтобы определить, когда тест останавливается. Если моделируемое E-значение пересекает 1/α = 20, тест останавливается с отклонением H0. Если эффект не обнаружен, тест останавливается при силе 1 - β = 0,8, так как эта сила распространена в промышленности. На рисунке 3 показано моделирование времени остановки и решений безопасного теста по сравнению с t-тестом.
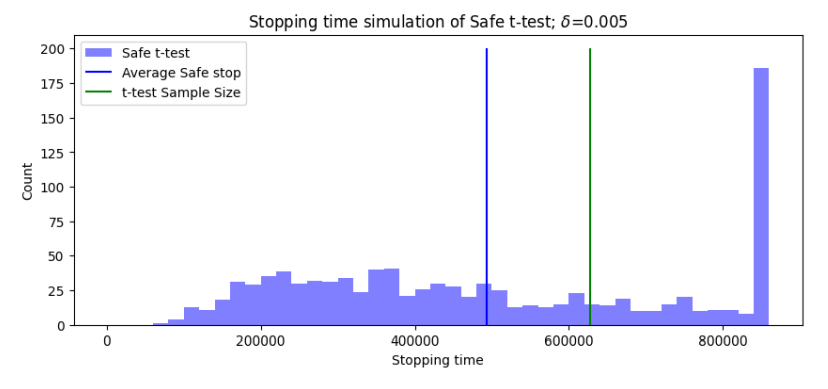
Как мы видим из среднего времени остановки на рисунке 3, в Safe T-тесте используется менее 500 000 образцов для достижения статистически достоверных результатов, в то время как классический T-критерий требует более 600 000. Тем не менее, размер выборки, необходимый для достижения 1-β-мощности для безопасного t-критерия, составляет приблизительно 850 000, что намного больше, чем у классического t-критерия. Можно спросить, приемлемо ли просто провести безопасное t-критерий до классического размера образца T-теста. На рисунке 4 (слева) показано влияние этого действия на статистические ошибки. При завершении теста как классический t-критерий, так и безопасное t-критерий соответствуют требованию, чтобы ошибки типа I ниже α = 0,05, а ошибки типа II ниже β = 0,2. Тем не менее, объединение двух тестов приводит к частоте ошибок типа I и, следовательно, не будет соответствовать ожидаемому уровню статистической значимости экспериментатора. Учитывая сбережения в продолжительности теста, может быть мотивация разработки методов объединить эти тесты в будущем, так что ложная положительная скорость остается ниже α, например, с использованием коррекции Бонферрони.
Помимо общих выводов двух тестов, интересно рассмотреть эксперименты, для которых классический t-критерий и безопасный T-критерий не согласны. Как видно на рисунке 4 (справа), в то время как оба теста достигают 80% мощности, они делают это по -разному. Многие симуляции, для которых классический T-критерий принимает H0, отвергается безопасным T-тестом, и наоборот. Эта разница в результатах, вероятно, будет трудно усвоить для практикующих, которые рассматривают возможность
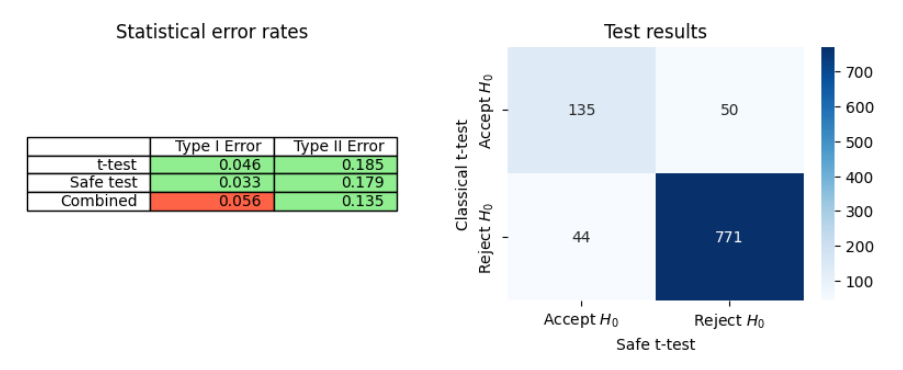
T-тест, который является источником истины для их платформы.
Хотя рисунок 3 оценивает безопасное время остановки для фиксированного размера эффекта, важно рассмотреть результаты для широкого диапазона величин эффекта. Чтобы объединить результаты величины эффекта от 0,01 до 0,3, мы нормализуем время остановки по времени остановки t-критерия. Результаты этого анализа можно увидеть на рисунке 5.
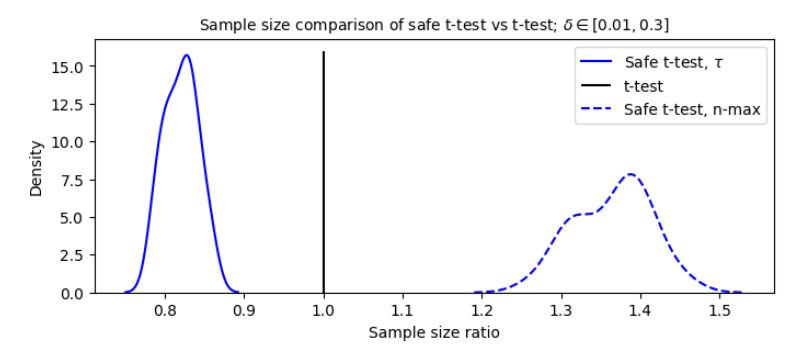
На рисунке 5 показана как средняя остановка безопасного t-теста, так и размер выборки, необходимый для 80% мощности. В среднем, Safe Test использует на 18% меньше данных, чем T-критерий. Однако для достижения той же мощности в 80% в безопасном тесте используется на 36% больше данных. Учитывая, что большинство тестов A/B не приводят к отказу от H0 [Aze+20], это может привести к более длительным экспериментам в целом для практиков.
4.4 Сравнение χ2 -теста с тестом на безопасную пропорцию

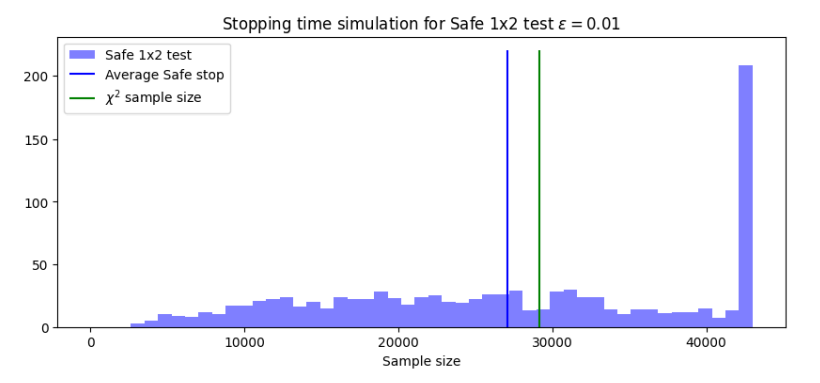
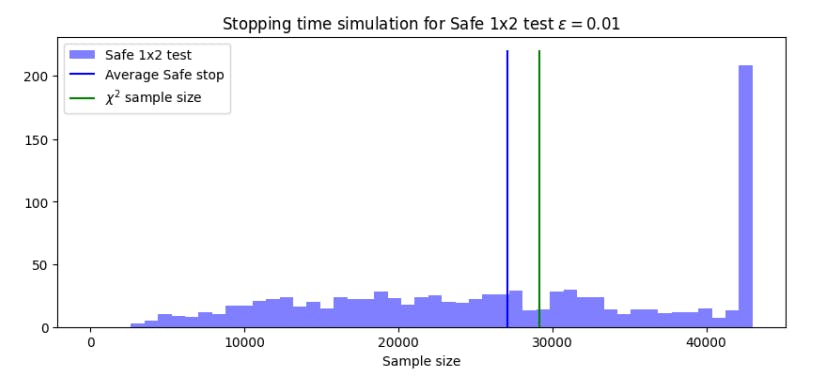
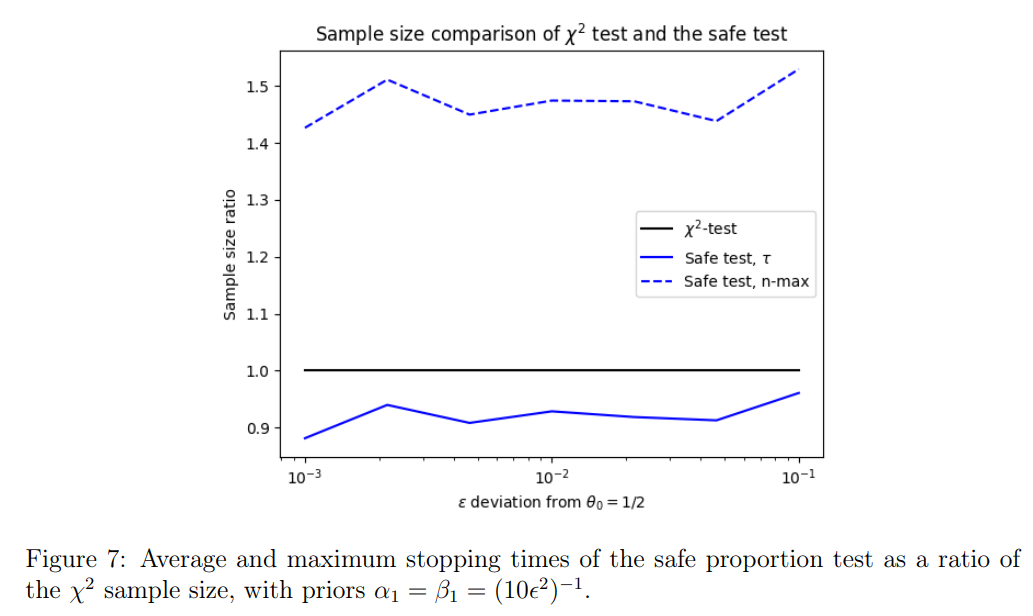
Результаты рисунка 6 удивительно похожи на результаты, которые можно увидеть, сравнивающие t-критерий и безопасное t-критерий на рисунке 3. В безопасном тесте в среднем используется меньше образцов, чем его классическая альтернатива, в то время как максимальное время остановки для достижения требуемой мощности выше. Затем мы рассматриваем размеры выборки тестов как функцию разницы ϵ. На рисунке 7 показано как среднее, так и максимальное время остановки для ϵ ∈ [0001, 0,1].
Как видно на рисунке 7, средний размер выборки, необходимый для безопасной пропорции, меньше, чем у теста χ2 для всех значений ϵ. Это говорит о том, что безопасная пропорция будет конкурентоспособным с тестом χ2, даже для обнаружения небольших эффектов. Глядя на эти результаты, можно задаться вопросом, целесообразно ли установить предыдущий на основе неизвестного величины эффекта. Тем не менее, предварительный может основываться на величине эффекта, рассчитанного по данным после каждой выборки. Следовательно, установление априоров на основе текущего величины эффекта не оказывает влияния на достоверность теста.
В этом разделе мы сравнили безопасное t-критерий и безопасную тест на пропорцию с их классическими альтернативами. Было обнаружено, что средние размеры выборки для безопасного t-критерия меньше, чем у классического t-теста для широкого спектра величин эффекта. Тем не менее, максимальный размер выборки может быть намного больше для достижения той же статистической мощности. Кроме того, средние размеры выборки теста на безопасную долю меньше, чем у теста χ2. Эти результаты мотивируют дальнейшее принятие безопасных тестов в научных усилиях. В следующем разделе мы сравниваем безопасный t-критерий с другим тестом в любое время, используемом в промышленности, тесте последовательного отношения с последовательными вероятностью.
Автор:
(1) Даниэль Бизли
Эта статья есть
Оригинал

