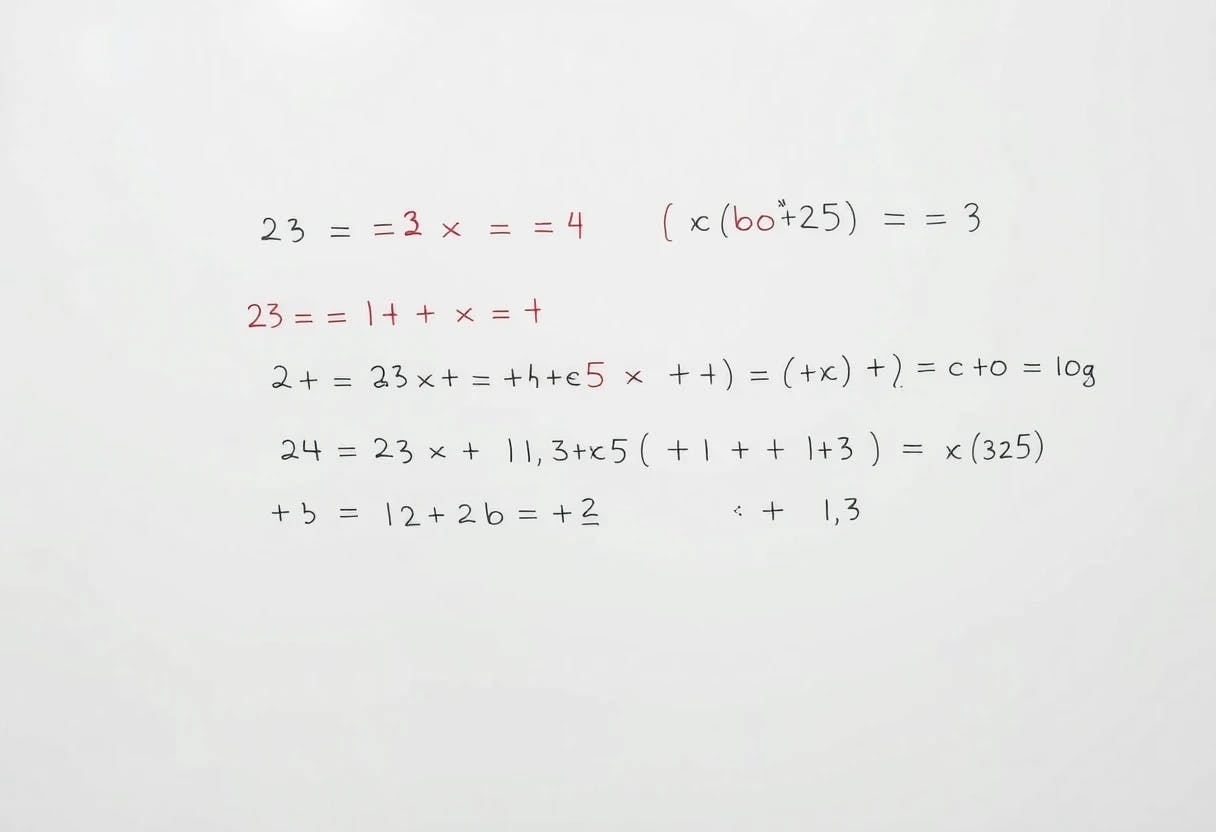
Как функциональные языки имитируют GOTO с этикетками и μ-связками
7 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Data is Dual to Codata
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
2.5 первоклассные функции
Основной функцией, которую мы пропустили до сих пор, являются первоклассные функции, которые характеризуются абстракциями Lambda 𝜆𝑥.𝑡 и функциональными приложениями 𝑡1 𝑡2. Но первоклассные функции не добавляют какую-либо выразительную силу в язык с типами кодатов, поскольку типы кодатов являются более общей концепцией, которая подчиняется функционирует в качестве особого случая. Поэтому мы могли бы реализовать абстракции Lambda и функциональные приложения в качестве синтаксического сахара как в веселье, так и в ядре. Кстати, это также то, что делали разработчики Java, когда они представили Lambdas для языка [Goetz et al. 2014]. Мы вводим Lambda Abstractions и Function Application с синтаксисом веселья и DeSugar их в коказы и деструкторы кодата с деструктором AP во время перевода в Core.

Пример 2.6. Рассмотрим термин (𝜆𝑥.𝑥 ∗ 𝑥) ⌜2⌝ в веселье. Мы можем перевести этот термин и оценить его в ядре следующим образом:
⟨Cocase {ap (𝑥, 𝛽) ⇒ ⟨𝜇𝛾. ∗ (𝑥, 𝑥; 𝛾) | 𝛽⟩} | AP (⌜2⌝; ⋆)⟩ ⊲ ⟨𝜇𝛾. ∗ (⌜2⌝, ⌜2⌝; 𝛾) | ⋆⟩ ⊲ ∗ ⟨⌜4⌝ | ⋆⟩
2.6 Операторы управления
Наконец, мы добавляем функцию, которую мы использовали в мотивирующем примере во введении: этикетки и прыжки. Мы должны расширить удовольствие от конструкций Label и Goto, но, поскольку мы можем перевести их на локальном уровне в 𝜇-связки, нам не нужно что-то добавлять в ядро.

Термин «метка» {𝑡} связывает ковейскую 𝛼 в термине 𝑡 и, таким образом, предоставляет место, в которое можно прыгать в 𝑡 𝑡 𝑡. Такой Goto (𝑡; 𝛼) принимает местоположение 𝛼 в качестве аргумента, а также термин 𝑡, который следует использовать для продолжения вычислений в месте, где 𝛼 был связан. Немного сложно записать точно, как работает оценка метки и готео, но следующие два правила являются хорошим приближением, где мы предполагаем, что 𝛼 не происходит свободным в 𝔱:
Метка 𝛼 {𝔱} ⊲ 𝔱 Метка 𝛼 {. Полем Полем goto (𝔱; 𝛼). Полем .} ⊲ 𝔱
В левом правиле говорится, что, когда помеченный термин 𝑡 можно оценить до значения 𝔱, не используя GOTO, мы можем отказаться от окружающей этикетки. Правило справа гласит, что если у нас есть Goto, который прыгает на этикетку 𝛼 со значением 𝔱, то мы отбрасываем все между меткой и Goto и продолжаем вычисление с этим значением 𝔱. Чтобы сделать это второе правило точным, мы должны ясно сделать то, что мы указываем только с эллипсами, отделяющими этикетку от прыжка; Мы сделаем это в разделе 3.
Пример 2.7.Во введении мы использовали пример функции быстрого умножения, которая умножает все элементы списка и коротко замыкает вычисление, если оно сталкивается с ноль. Поскольку мы позволили определениям верхнего уровня передавать ковариации в качестве аргументов, теперь мы можем написать пример введения.
дефектMult (𝑙) ≔этикетка𝛼 {mult ’(𝑙; 𝛼)}
дефектMult ’(𝑙; 𝛼) ≔случай𝑙из{Nil ⇒ 1, минусы (𝑥, 𝑥𝑠) ⇒IFZ(𝑥,goto(0; 𝛼), 𝑥 ∗ mult ’(𝑥𝑠; 𝛼))}
Когда мы переводим наОсновнойи упростите полученный термин, мы получаем результат:
def mult (𝑙; 𝛼) ≔ mult ’(𝑙; 𝛼, 𝛼)
def mult ’(𝑙; 𝛼, 𝛽) ≔
⟨𝑙 | case {nil ⇒ ⟨1 | 𝛽⟩, минусы (𝑥, 𝑥𝑠) ⇒ ifz (𝑥, ⟨0 | 𝛼⟩, ∗ (𝑥, 𝜇𝛾 .mult ’(𝑥𝑠; 𝛼, 𝛾); 𝛽))}⟩
Это почти тот результат, который мы видели во введении. Единственное отличие состоит в том, что рекурсивный призыв к мульти вложен в умножение. Это та же проблема, которую мы видели с вложенными арифметическими операциями в конце раздела 2.1, и мы рассмотрим ее в следующем разделе.
Оператор управления меткой/GOTO, который мы представили в этом подразделе, конечно, назван в честь инструкций и этикетки GOTO, которые можно найти на многих императивных языках программирования. Наша адаптация к контексту языков функционального программирования аналогична классическим операторам контроля (см. Раздел 5.3 для более точного обсуждения), таких как J [Landin 1965] или Let/CC (также известный как Escape) [Reynolds 1972]; Язык программирования Scala также обеспечивает тесно связанную границу/разрыв [3], где граница отмечает блок кода, на который программист может прыгать с помощью инструкции по разрыву. Одно центральное свойство этого контрольного эффекта заключается в том, что оно лексически ошеломлено, поскольку имена метки 𝛼 передаются вокруг лексически и могут быть затенены. Это отличает их от динамически общекартовых операторов управления, таких как механизмы исключений, найденные во многих языках программирования, таких как Java или C ++. (Динамически окрашенный вариант нашего оператора управления будет опустить имена метки, и прыжок в метке {... goto (𝑡) ...} вернется к ближайшему оболочению метки во время выполнения.) Мы следуем за более поздней переоценкой лежальной области управления, например, от Zhang et al. [2016] В случае исключений или Brachthäuser et al. [2020] В случае обработчиков эффекта и разграниченных продолжений.
Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Оригинал

