Как электронные варибления предотвращают ложную положительную инфляцию
12 августа 2025 г.Таблица ссылок
Введение
Гипотеза тестирование
2.1 Введение
2.2 Байесовская статистика
2.3 тестируйте мартингингинг
2.4 P-значения
2.5 Дополнительная остановка и взгляды
2.6 Сочетание P-значений и дополнительного продолжения
2.7 А/б -тестирование
Безопасные тесты
3.1 Введение
3.2 Классический T-критерий
3.3 Безопасный T-критерий
3.4 χ2 -test
3,5 безопасного теста на пропорцию
Безопасное моделирование тестирования
4.1 Введение и 4.2 реализация Python
4.3 Сравнение t-теста с безопасным t-тестом
4.4 Сравнение χ2 -теста с тестом на безопасную пропорцию
Смесь последовательного теста вероятности
5.1 Последовательное тестирование
5.2 Смесь SPRT
5.3 MSPRT и безопасный T-критерий
Онлайн -контролируемые эксперименты
6.1 Безопасный t-тест на наборах данных OCE
Vinted A/B-тесты и 7.1 Safe T-критерий для Vinted A/B-тестов
7.2 безопасная пропорция для несоответствия соотношения образца
Заключение и ссылки
3 безопасные тесты
3.1 Введение
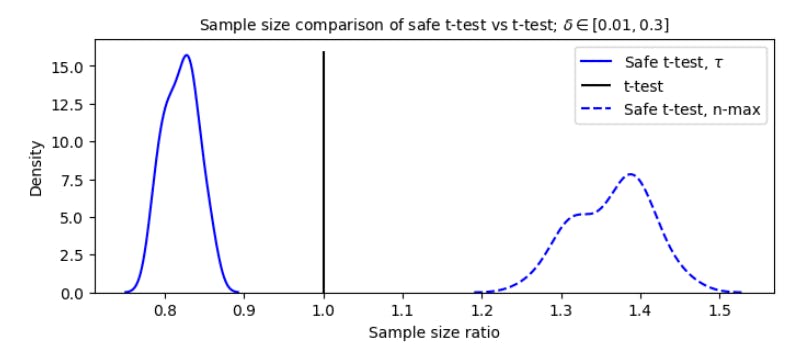
Безопасное тестирование [GHK23] - это новый метод тестирования гипотез, разработанный для решения многих проблем с современным статистическим выводом. АбезопасныйВ безопасном тестировании относится к тому факту, что ложная положительная скорость не увеличивается выше α в необязательных условиях продолжения. Как мы увидим, многие безопасные тесты также позволяют предоставлять дополнительную остановку [GHK23], в частности, те, которые мы будем применить к безопасному t-критерию и безопасному тесту пропорции. На рисунке 2 показано, как ложно положительная скорость безопасного t-теста изменяется по сравнению с экспериментом.
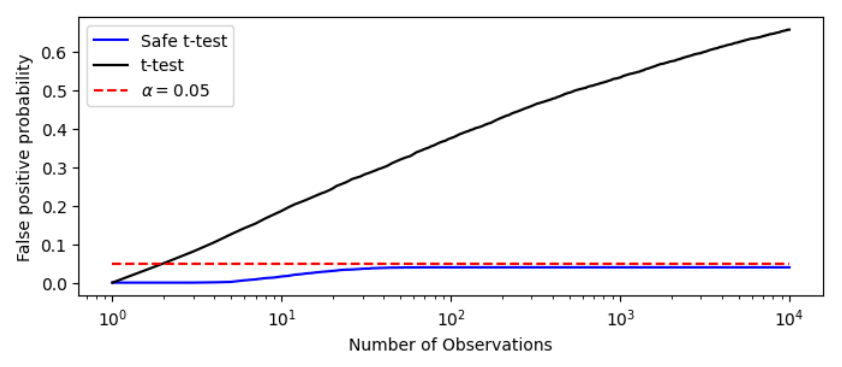
Безопасное тестирование основано наЭлектронныеили (e-test Statistics), которые являются неотрицательными случайными переменными, которые удовлетворяют
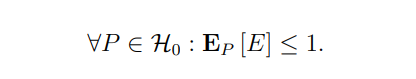
Согласно нулевой гипотезе, многие электронные разнообразные ведут себя как тест Мартингейлс [GHK23], которые тесно связаны с байесами.

В дополнение к этой интуитивной интерпретации, электронные районы также обеспечивают много математических преимуществ. Ранее мы выделили значения p, дополнительную остановку и дополнительное продолжение в качестве нескольких проблем с классическим статистическим тестированием. Сейчас мы продолжаем обсуждать эти вопросы в контексте электронных изменений.


Для ситуаций, в которых величины эффекта неизвестны или для тестов с параметрами неприятностей, рост может быть неопределенным. Тем не менее, оптимальный рост может быть определен относительно неизвестного параметра. Электронная переменная с этим свойством известна какродственникРАСТИ. Эти концепции будут применяться в производных статистике Safe T-Statatistic и безопасной пропорции.
Несмотря на то, что существуют электронные районы, которые небезопасны при дополнительной остановке [GHK23], A/B-тестирование использует довольно распространенные статистические тесты, для которых доступны дополнительные электронные варибные помещения. Первый такой тест, который мы рассмотрим,-это t-критерий, начиная с теории, стоящей за классическим t-тестом.
3.2 Классический T-критерий

Т-статистика в преобразовании в p-значение с использованием T-распределения с ν = N+M-2 градусам свободы,
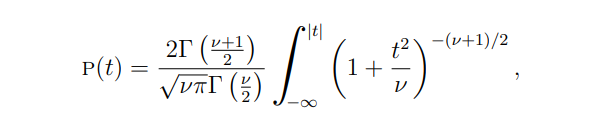
который затем используется для принятия решения о гипотезе.
Размер выборки для t-теста определяется как α, β и величины эффекта Δ. Прежде чем собирать данные, величина эффекта неизвестен и должен быть оценен. После теста величина эффекта может быть рассчитана с помощью D Cohen, который представляет общую разницу между группами
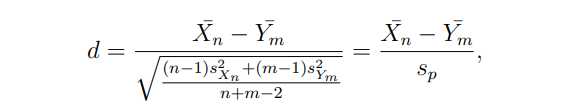
где SP - объединенное стандартное отклонение
3.3 Безопасные Т-Тес

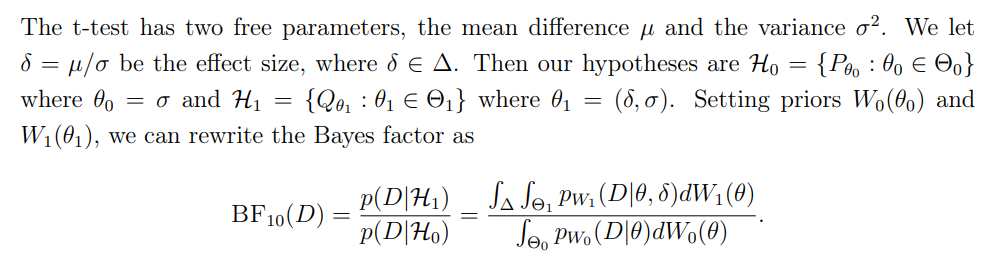

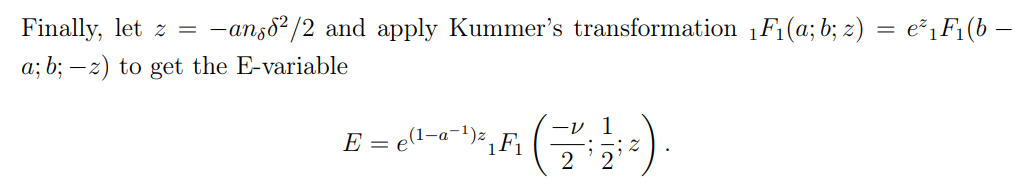
Было показано, что односторонняя статистика Safe T-теста выращивается, а двухсторонняя статистика испытаний была относительной ростом [Pér+22]. Далее мы обсудим тест χ2 и его безопасную альтернативу.
3,4 χ2-теста
Тест χ2 представляет собой классический статистический тест, который используется для оценки распределения ячеек таблицы непредвиденных обстоятельств. Таблица на случай непредвиденных обстоятельств содержит частоты многономиальных данных, что позволяет оценивать сходства параметров двух распределений. В случае биномиальных данных таблица непредвиденных обстоятельств составляет 2x2, что будет в центре внимания этого раздела.

Статистика χ2 в преобразовании в p-значение с использованием распределения χ2 с (r-1) (c-1) степенью свободы, где r и c являются количеством рядов и столбцов в таблице. Как и в случае классического t-теста, χ2 не является безопасным при дополнительной остановке, и, таким образом, заглядывание может надуть их ложную положительную скорость [xu+22]. По этой причине были разработаны безопасные альтернативы, которые позволяют разработать выводы в любое время, которые мы рассмотрим сейчас.
3,5 безопасного теста на пропорцию

Далее рассмотрим количество
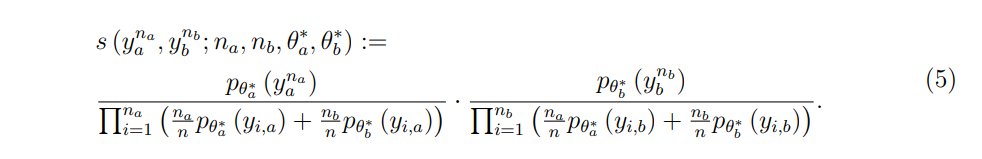


и n1 = na1 + nb1. Под H1 совместное распределение
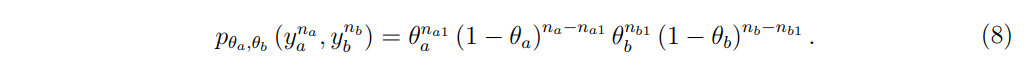
Объединение 6, 7 и 8 и упрощение (подробности см. [TLG22]) дает окончательное выражение для относительного выращивания E-vairate размера партии Na + NB:
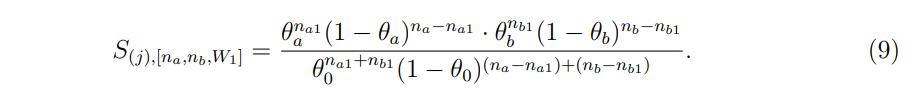
В следующем разделе мы сравниваем безопасный T-критерий и безопасную тест на пропорцию с их классическими альтернативами.
Автор:
(1) Даниэль Бизли
Эта статья есть
Оригинал

