Может ли финансовая модель по -настоящему имитировать реальность? Эти цифры говорят да

28 июля 2025 г.

Таблица ссылок

Аннотация, подтверждения, а также заявления и декларации

1. Введение

2. Фон и связанная работа

   2.1 Моделирование финансового рынка на основе агента

   2.2 Эпизоды флэш -аварии

3. Структура модели и настройка модели 3.1

   3.2 Общее поведение трейдеров

   3.3 Фундаментальный трейдер (Ft)

   3.4 Momentum Trader (MT)

   3,5 шумового трейдера (NT)

   3.6 Market Maker (MM)

   3.7 Динамика моделирования

4. Калибровка и проверка модели и целевая калибровка 4.1: данные и стилизованные факты для реалистичного моделирования

   4.2 Калибровочный рабочий процесс и результаты

   4.3 Проверка модели

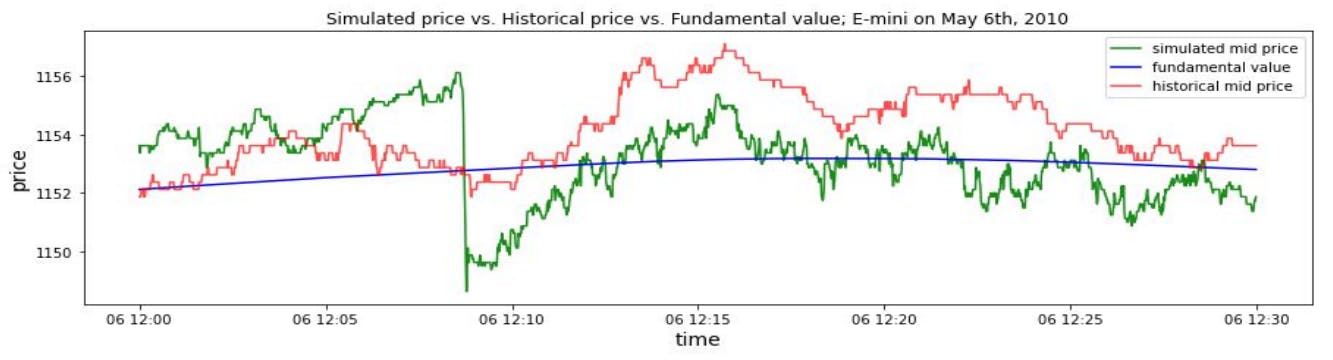
5. Сценарии флэш -аварии 2010 года и 5,1 моделирования исторической флэш -аварии

   5.2 Флэш -авария в разных условиях

6. Мини -флэш -сценарии аварии и 6.1 Внедрение трейдера Spiking (ST)

   6.2 Анализ мини -флэш -аварии

   6.3 Условия для сценариев аварии мини -флэш -авара

7. Заключение и будущая работа

   7.1 Сводка достижений

   7.2 Будущие работы

Ссылки и приложения

4.3 Проверка модели

В таблице 2 показано стилизованное расстояние от калиброванной модели. Тем не менее, само значение не представляет интуитивного описания того, насколько хорошо моделируемые данные соответствуют эмпирическим данным. Требуется перекрестная проверка на обоснованность нашей модели топологии и стратегии калибровки. После Franke and Westerhoff (2012) два метрика используются для оценки качества соответствия момента и обоснованности моделирования модели: специфическое для момента p-значение и моментное соотношение охвата.

4.3.1 Статистическое тестирование гипотезы: специфическое для момента p-значение

Стилизованное расстояние фактов дает нам численные значения для реализма симуляции. Тем не менее, необходимо решить еще один элементарный вопрос: будут ли эмпирические данные отклонены еще один элементарный вопрос. На вопрос отвечает расчет моментного значения P в качестве статистического теста гипотезы.

Напомним, что в разделе 4.1.4 веса рассчитываются методом начальной загрузки блока, предложенного в Franke and Westerhoff (2012). В то время как дисперсия образцов начальной загрузки блока является соответствующим весом для каждой части функции потери, большое количество образцов, полученных в этой процедуре, также может использоваться для применения функции потери D к им. Таким образом, доступно целое частотное распределение значений D, которое впоследствии может противопоставить моделируемому распределению значений D. Основная идея заключается в том, что набор загрузочных образцов временных рядов возврата представляет собой прокси из различных образцов временных рядов возврата, который может быть произведен в случае гипотетического процесса генерации данных в недалью. Соответственно, если смоделированное время возврата дает значение D в диапазоне загрузочных значений D, этот моделируемый временной ряд возврата трудно отличить от реальной серии.

Из таблицы 3 мы видим, что для всего торгового дня в собранном наборе данных, специфичные для момента p-значения превышают 0,05. Следовательно, мы не можем отклонить нулевую гипотезу, которая указывает, что моделируемый временной ряд возврата принадлежит к тому же распределению, что и эмпирический временной ряд возврата. Это статистическое тестирование гипотез дает доказательства того, что калиброванная модель способна генерировать реалистичные финансовые временные ряды.

4.3.2 Моментный коэффициент покрытия

Предыдущая оценка модели была основана на значениях стилизованной функции расстояния фактов D. Хотя статистическое тестирование позволяет нам оценивать достоверность моделирования модели, качество соответствия момента для каждого конкретного момента до сих пор неизвестно. Другая потенциальная проблема заключается в том, что стилизованная функция расстояния фактов D является целью оптимизации в процессе калибровки. Таким образом, метрика оценки с участием расстояния D может быть смещена из -за проблемы с переосмыслением. Чтобы решить вышеуказанные проблемы, принят показатель «Коэффициент охвата момента» (MCR) для оценки степени соответствия момента, принимая во внимание каждый конкретный момент. Моментный коэффициент покрытия первоначально предложен в Franke and Westerhoff (2012). Основой для расчета коэффициента охвата момента является концепция доверительного интервала эмпирических моментов. В соответствии с Franke и Westerhoff (2012), рассматривается 95% доверительный интервал момента, который определяется как интервал с границами ± 1,96 раза превышать стандартное отклонение вокруг эмпирического значения этого момента. Следующим шагом является определение стандартного отклонения для каждого эмпирического момента. Franke and Westerhoff (2012) применяют метод Delta к коэффициентам автокорреляции для расчета стандартного отклонения. В этой статье мы используем более прямой способ получить эмпирическое стандартное отклонение, которое основано на методе начальной загрузки блока. Напомним, что большое количество временных рядов возврата получается методом начальной загрузки блока. Для каждого конкретного момента значение момента может быть рассчитано из каждой серии возврата отбирателей. В общей сложности будут значения B для каждого момента, когда B является номером образец начальной загрузки. Стандартное отклонение этих значений считается стандартным отклонением для соответствующего эмпирического момента. Можно чувствовать себя неловко по поводу начальной загрузки функций автокорреляции при более длинных лагах, поскольку метод изменяет временный порядок серии возврата. Тем не менее, размер блока в нашем методе начальной загрузки блока составляет 1800, что значительно больше, чем самая длинная задержка (90) в функциях автокорреляции. Следовательно, влияние загрузочного блока на функции автокорреляции незначительно.

Со стандартным отклонением под рукой соответствующий доверительный интервал для каждого конкретного момента сразу же доступен. Таким образом, получен интуитивно понятный критерий для оценки моделируемой серии возврата: если все его моменты содержатся в доверительных интервалах, моделируемая серия возврата не может быть отвергнута как несовместимая с эмпирическими данными. Тем не менее, одного моделирования недостаточно для оценки модели в целом из -за изменчивости выборки. Кроме того, вполне вероятно, что для одной моделируемой серии возврата некоторые моменты содержатся в доверительном интервале, а другие - нет. Само собой разумеется, что с учетом нескольких прогонов моделирования модели обеспечит более исчерпывающую оценку производительности модели. В частности, для каждого моделирования запустите проверку доверительного интервала повторяется. Мы подсчитаем количество прогонов моделирования Монте -Карло, в которых одиночные моменты содержатся в соответствующих доверительных интервалах. Соответствующие процентные числа из всех пробежек Монте -Карло определяются как моментный коэффициент покрытия.

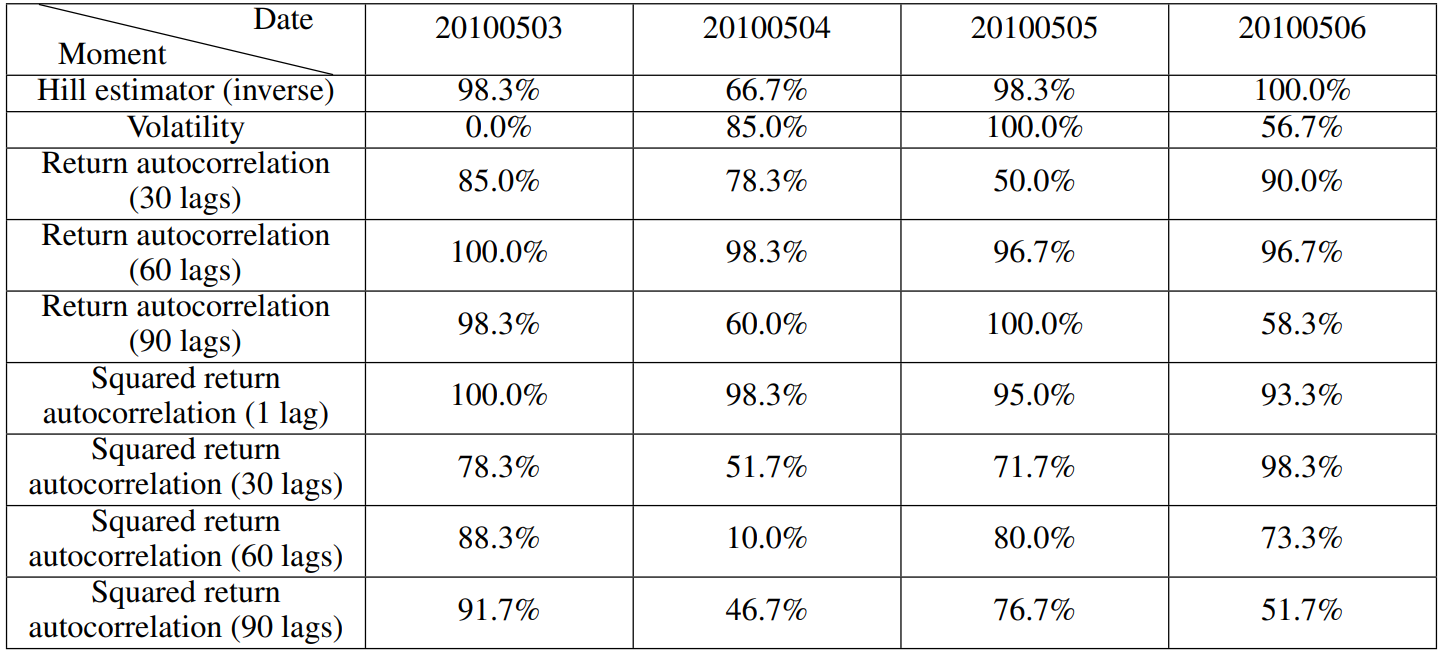
Поскольку модель откалибрована каждым торговым днем, моделирование Монте -Карло выполняется для каждого торгового дня, а соответствующие коэффициенты охвата момента рассчитываются для оценки калиброванной модели. В таблице 4 представлены результаты момента расчета коэффициентов охвата. За исключением момента волатильности 3 мая и момента автокорреляции в квадрате 90-полосных классов 4 мая, все другие коэффициенты охвата момента выше 50%. Согласно анализу в Franke and Westerhoff (2012), коэффициент охвата моментом выше 50% представляет собой потрясающую производительность модели. Кроме того, почти половина моментов коэффициенты охвата даже выше 90%, что указывает на то, что наша калиброванная модель обладает превосходной способностью воспроизводить реалистичные стилизованные факты. В целом, в отношении выбранных моментов способность калиброванной модели сопоставлять эмпирические моменты и воспроизводить реалистичные стилизованные факты очень примечательны.

---

---

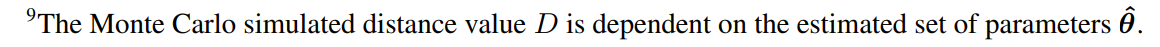
Оригинал