Руководство для начинающих по тестированию гипотез и байесовской статистике
12 августа 2025 г.Таблица ссылок
Введение
Гипотеза тестирование
2.1 Введение
2.2 Байесовская статистика
2.3 тестируйте мартингингинг
2.4 P-значения
2.5 Дополнительная остановка и взгляды
2.6 Сочетание P-значений и дополнительного продолжения
2.7 А/б -тестирование
Безопасные тесты
3.1 Введение
3.2 Классический T-критерий
3.3 Безопасный T-критерий
3.4 χ2 -Test
3,5 безопасного теста на пропорцию
Безопасное моделирование тестирования
4.1 Введение и 4.2 реализация Python
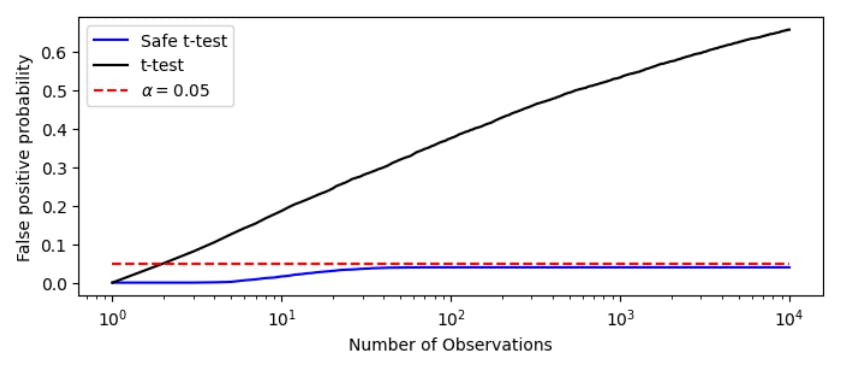
4.3 Сравнение t-теста с безопасным t-тестом
4.4 Сравнение χ2 -теста с тестом на безопасную пропорцию
Смесь последовательного теста вероятности
5.1 Последовательное тестирование
5.2 Смесь SPRT
5.3 MSPRT и безопасный T-критерий
Онлайн -контролируемые эксперименты
6.1 Безопасный t-тест на наборах данных OCE
Vinted A/B-тесты и 7.1 Safe T-критерий для Vinted A/B-тестов
7.2 безопасная пропорция для несоответствия соотношения образца
Заключение и ссылки
2 Гипотеза тестирование
2.1 Введение
Гипотеза тестирование - это метод науки о назначении истины. Начиная с нулевой гипотезы, указывающей на текущее убеждение, цель теста состоит в том, чтобы определить, отверг ли или нет нулевую гипотезу [LR05]. Решение основано на реализации случайной величины x с распределением pθ, где Pθ принадлежит классу {pθ: θ ∈ θ}. Этот класс гипотезы разделен на области, которые принимают или отвергают гипотезу. Для нулевой гипотезы h0 мы позволяем θ0 представлять подмножество θ, для которой H0 является истинной, и θ1 - подмножество, для которого H0 является ложным. Это эквивалентно записи θ ∈ θ0 и θ ∈ θ1 соответственно. Может быть альтернативная гипотеза H1 = {pθ: θ ∈ θ1} к нулевой гипотезе H0. В байесовской формулировке тестирования гипотез всегда есть альтернативный H1, хотя это не требуется во всех частых составах. Если θ1 = {θ1}, одна точка, то H1 называется простым. И наоборот, если | θ1 | > 1, тогда H1 составлен. Обозначение H0: θ = θ0 - конденсированный способ написания h0 = {pθ: θ = θ0}.
Результат теста исходит от функции принятия решения Δ (x), которая может принять значение D0 для принятия H0 или значения D1 для отклонения H0. Поскольку проблема тестирования гипотез является стохастической, всегда существует возможность совершения одной из двух ошибок. Первый тип ошибки возникает, когда нулевая гипотеза отвергается, когда она истина, то есть (x) = d1 для некоторого θ ∈ θ0. Это известно как ошибка типа I или ложный положительный. Статистические испытательные границы. Вероятность ошибки типа I по уровню значимости α, которая представляет максимальную вероятность возникновения этой ошибки. Математически это написано как
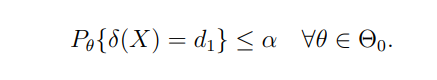
Второй тип ошибки возникает, когда гипотеза не отклоняется, когда она ложна: Δ (x) = d0, когда θ ∈ θ1. Эта ошибка известна как ошибка типа II или ложный отрицательный результат. Для любого классического статистического теста это также будет иметь ненулевую вероятность β:
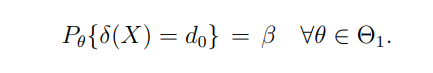
Количество 1 - β известно как сила теста. Это вероятность того, что тест правильно отвергает гипотезу в том случае, что он ложный. Для данного α мы стремимся максимизировать мощность, которая зависит от размера выборки эксперимента.
Размер выборки эксперимента - это количество образцов, которые необходимо собрать, чтобы принять решение. В процессе разработки классического эксперимента экспериментатор обычно будет заранее определять размер выборки. Это требует оценки трех величин: уровень значимости α, мощность 1 - β и неизвестный величина эффекта δ. Размер эффекта - это разница между двумя группами субъектов, часто сочетанием их средней разницы и их отклонений. Размер эффекта может быть оценен, когда он является неизвестным количеством или фиксированным до минимального соответствующего величины эффекта, например, в клинических исследованиях. Снижение любого из трех величин α, β или Δ приведет к большим размерам образцов для экспериментов и аналогично увеличивает приводят к меньшим размерам образцов.
Исторически, большая часть статистического тестирования была сосредоточена на частых статистике, однако байесовская статистика предлагает бесценные методы обучения на данных. Затем мы более глубоко рассмотрим концепции байесовской статистики.
2.2 Байесовская статистика

Соотношение маргинальных распределений относительно альтернативной гипотезы H1, а нулевая гипотеза H0 известна как байесовский фактор:
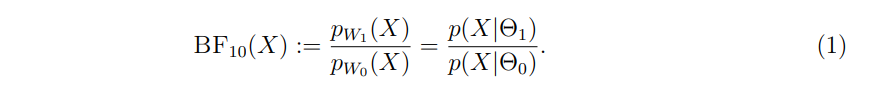
Байесовский фактор можно рассматривать как количество доказательств в пользу альтернативы против нуля. Как мы увидим, байесовские факторы замысловато связаны с безопасным тестированием. Другая важная концепция в этой теории - это концепция тестирования мартингал.
2.3 тестируйте мартингингинг

Теперь мы продолжим обсуждение тестирования гипотез с печально известным значением P.
Автор:
(1) Даниэль Бизли
Эта статья есть
Оригинал

