Алгоритм доказательства с нулевым разглашением: протокол ZK-Stark-FRI

Предисловие

Наконец, мы подошли к заключению серии «Понимание ценности алгоритма доказательства с нулевым разглашением — Zk-stark». Мы обсуждали общую структуру алгоритма Zk-Stark, первую часть алгоритма, арифметизацию, и вторую часть алгоритма, низкоуровневое тестирование, в предыдущих трех статьях. Я считаю, что после прочтения этих статей у вас будет общее представление об алгоритме Zk-Stark. Однако вы можете усомниться в точности некоторых предложений или иллюстраций в статье. Действительно, для определенного содержания требуется более конкретное введение и пояснение. В противном случае могут возникнуть недоразумения.

В третьей статье мы обсудили важность проведения LDT для полиномов, чтобы гарантировать, что значения, возвращаемые доказывающим, удовлетворяют равенству полиномиальных уравнений и действительно вычисляются с использованием эффективных полиномов. Тем временем, чтобы свести к минимуму сложность верификатора, мы преобразовали исходный полином, и, таким образом, полином, который должен быть проверен верификатором, составляет только половину исходного полинома. Повторяйте до тех пор, пока степень многочлена не может быть определена напрямую. Это основная концепция протокола FRI. Теперь давайте подробно рассмотрим протокол FRI.

Протокол FRI

FRI, Fast RS IOPP или Fast Reed—Solomon Interactive Oracle Proofs of Proximity — это более эффективный метод проверки близости, который используется для определения того, находится ли набор точек в основном на полиноме со степенью меньше заданной. значение и может достичь линейной сложности доказательства и логарифмической сложности проверки или нет. Прежде чем мы представим протокол FRI полностью, давайте рассмотрим простой сценарий.

Существует мультипликативная группа L_0 порядка 2^n на поле Галуа F.

• В этот момент доказывающая сторона утверждает, что кодовое слово f_0: L_0−>F удовлетворяет параметру RS[F,L_0,ρ] кодирования, то есть большинству точки в f_0 лежат на многочлене P(x) порядка ; здесь ρ=2^(−R);

В результате, когда f_0=P, существуют многочлены deg(P1,P2)<1/2∗ρ∗2^n , порядок которых удовлетворяет соотношению и удовлетворяет следующему уравнение:

f_0(x) = P(x) = P1(x^2) + xP2(x^2)(1)*

Положим Q(x, y)=P1(y)+x∗P2(y) мы увидим порядок d<2 двоичного многочлена Q(x, y ) относительно переменной x; Порядок d<1/2∗ρ∗2^n. переменной y, а когда y=x^2, существует Q(x, y)=f_0(x); В это время верификатор V случайным образом выбирает значение x0x0 и отправляет его проверяющему P. Доказательство P вычисляет Q(x_0,y) и устанавливает:

f1(y)=Q(x_0, y)=P1(y)+x_0*P2(y)(2)

Для многочлена f1(y), поскольку y=x^2 и x имеет диапазон значений группы L_0, таким образом, существует представляет собой уравнение x^(2^n)=1, которое можно преобразовать в (x^2)^n=1. Следовательно, если диапазон значений независимой переменной y определен как Группа L1, то L1 должен обладать следующими свойствами:

• Порядок группы 2^(n−1);

• Каждый элемент группы L1 соответствует двум элементам группы L_0; то есть для любого элемента y группы L1 существуют два элемента x и (−x) mod p в группе L_0, удовлетворяющих условию x^2 mod p = y&&(−x)^2 mod p = y;

Пока вопрос трансформируется в вопрос, в котором доказывающая P должна доказать, удовлетворяет ли порядок полинома f1(y) d<1/2∗ρ∗ 2^n или нет; при этом должна быть обеспечена согласованность функций f1 и f0. Конкретные шаги заключаются в следующем:

• Проверяющий V выбирает три точки y,s0,s1 из группы L_1 и группы L_0 для удовлетворения s0 !=s1&&s0^2 = s1^2 = у

• Доказательство P возвращает три значения f0(s0), f0(s1), f1(y).

• Верификатор V интерполирует полином g(x) порядка d<2 в соответствии с f0(s0) , f0(s1) .

• Верификатор V подтверждает g(s0)=f1(y), и, если они не равны, проверка завершается неудачно.

• //2022-01-11 Описание ошибки g(x^0)=f1(y) было изменено.

Анализ надежности: если функция f1 не преобразуется из функции f0 в соответствии с описанным выше процессом, то с большой вероятностью полином P1( x2) и P2(x2) формулы (1) и многочленов P1(y) и P2(y) формулы (2) не равны друг другу. Учитывая, что порядок полинома удовлетворяет d<1/2∗ρ∗2n, а диапазон значений переменной равен 2(n−1), вероятность равенства полином (1/2∗ρ∗2^n/2^(n−1))=ρ если значение выбирается случайным образом в пределах этого диапазона в соответствии с теоремой Шварца-Циппеля. ρρ представляет кодовые скорости. Если ρ=2^−8, то вероятность успешной проверки только один раз составляет просто 2^−8. Если он проверен kk раз, то вероятность успеха в работе с невоспитанностью равна 2^−8k.** При увеличении значения kk вероятность бесконечно близка к 0.

Повторяйте описанный выше процесс для функции f1 до тех пор, пока многочлен fr не станет формой, которая может эффективно оценивать порядок, и весь процесс LDT не будет завершен.

Далее давайте взглянем на конкретное содержимое протокола FRI, как показано на рисунке 1:

Протокол FRI разделен на два этапа: фиксация и запрос. Как видно из предыдущего примера простого сценария, процесс взаимодействия требует:

1. Верификатор V отправляет случайное число x0 проверяющему P;

1. Доказательство P создает новый многочлен fi

1. Верификатор V создает наборы точек s0,i,s1,i,yi запросов и отправляет их проверяющему P.

1. Доказательство P вычисляет соответствующие полиномиальные значения fi(yi) , *fi−1(s0,i), fi−1(s1,i)*

1. Верификатор V выполняет проверку достоверности.

Далее мы представим значение параметров и шагов в протоколах Commit и Query , а затем подведем итоги соответствующих процессов.

Совершить:

Общий ввод

• R : параметр коэффициента кодирования.

• i : индекс количества циклов

• r{: время цикла, значение (k0−R)/η

• η : параметр пространственного отображения x=>x^2^η

• Порядок L0:2^k0

• RS[F,Li,ρ] : Параметры кодирования [Поле Галуа, область охвата, коэффициент кодирования]

• q0(x) = x^2^η, Li+1 = q0(Li), Отображение из группы Li в группу Li+1

Доказательство ввода

• fi представляет вход функции цикла за время i.

• Li представляет группу, соответствующую циклу по времени ii, с порядком 2n−i

• RSi : параметры кодирования, соответствующие fi

LOOPi ≤ r

1. \

• xi : случайное число, отправленное верификатором V.

1. \

• Sy : каждый элемент группы Li+1 соответствует набору элементов группы Li.

• Py^i (X) : Полином, интерполированный на основе значения fi(x) на Sy

• fi+1(y)==Py^i (xi): указывает на согласованность между полиномами fi+1: и fi.

1. я==г

• Создание многочлена fr

• Интерполировать полином Pr(x)

• Вычислить порядок многочлена Pr(x)

• Сохранение коэффициентов a0,…,ad многочлена Pr(x)

• Конец этапа фиксации

1. я<г

• Сгенерируйте fi+1 в соответствии с методом расчета на шаге 2.

• Расчет приверженности полиномам fi+1

• Обновите соответствующие параметры и введите следующий цикл

Запрос:

Ввод верификатора

• См. Фиксацию для R/η/Li/RSi/xi/fi/P(x)

• l: количество запросов, повторяющихся несколько раз для достижения требуемого уровня безопасности$

Реконструировать fr

• Получите доступ к оракулу, чтобы получить a0,…,ad и реконструировать многочлен Pr(x)

• Рассчитать все значения P^r(x) в группе Lr и присвоить значения fr

Повторить l раз

• i = {0~r−1}

Si удовлетворяет набору si в si+1=q0(si)

Например, начиная с группы L0, случайным образом выберите элемент s0 и вычислите s1=q0(s0),, тогда s1 равно элемент группы L1. Однако существует также −s0 (при условии, что q0(x)=x2q0(x)=x2), удовлетворяющий приведенному выше соотношению в группе L0, поэтому существует S0= {s0,−s0}; Точно так же продолжайте повторять приведенные выше вычисления с s1 для r раз, и будет получен ряд наборов S0,S1,…,Sr−1 .

• i={0~r−1}

На множестве S0,S1,…,Sr−1, полученном на шаге 1, соответственно ЗАПРОСИТЬ значение многочлена fi

Убедитесь, что возвращаемое значение соответствует соответствующему полиномиальному обязательству (если обязательство на этапе COMMIT является вычислением хеш-функции на основе Меркла, то здесь для получения корня требуется несколько вычислений хеш-функции)

Интерполировать P0(x),P1(x),…,Pr−1(x) по очереди

• круговая проверка согласованности i={0∼−1}

Проверьте fi+1(si+1)=Pi(xi) последовательно

• Если все проверки прошли успешно, проверка проходит.

Затем установите η=1 (т.е. q0(x)=x2) в качестве примера для описания двухэтапного процесса протокола FRI, как показано на следующем рисунке:  d<ρ∗2^n

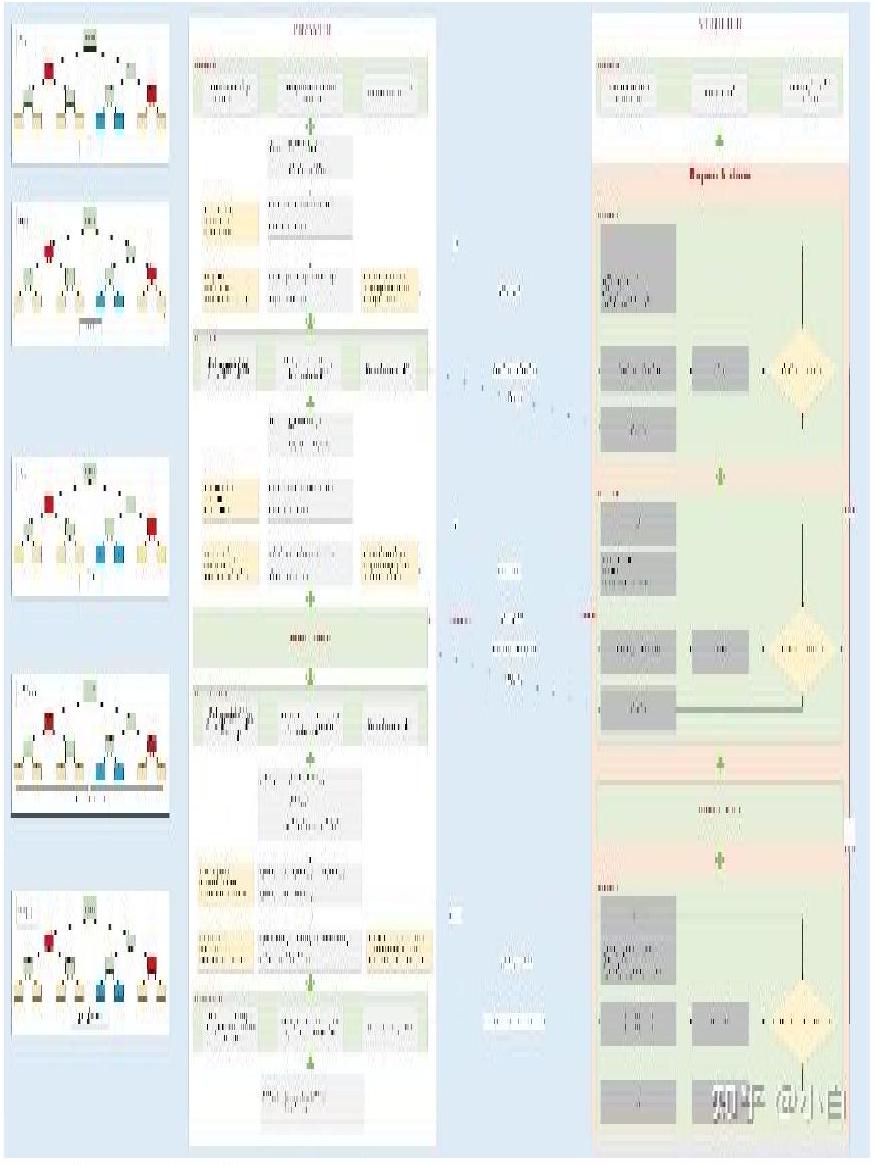
Как видно из описанного выше процесса:

• Для проверки непротиворечивости каждого раунда гарантируется, что исходный полином f0 удовлетворяет порядку d<ρ∗2^n .

• Если вышеуказанный протокол повторяется l раз, вероятность успеха людей, действующих с плохими манерами, может значительно снизиться.

Резюме

Описанный выше процесс представляет собой протокол FRI. Как видно, сложность проверки удовлетворяет логарифмическому соотношению . Алгоритм гарантирует, что циклические проверки непротиворечивости могут быть пройдены тогда и только тогда, когда исходный полином удовлетворяет условию . Фактическая реализация может незначительно отличаться. Для получения дополнительной информации см. документ DEEP-FRI. По сравнению с FRI, DEEP-FRI повышает надежность системы, сохраняя при этом оптимальный уровень сложности доказательства и проверки.

Основываясь на предыдущих трех статьях этой серии, алгоритм Zk-STARK можно резюмировать следующим образом:

1. Алгоритм разделен на две части: арифметизация и LDT.

1. Арифметизация преобразует задачу в полиномиальное равенство и полиномиальную задачу LDT.

1. Протокол FRI используется на этапе LDT для обеспечения сложности линейного доказательства и сложности логарифмической проверки.

1. гарантирует атрибут нулевого знания о том, что проверяющий не могут получить доступ к точкам в траектории полиноме и что траектория Полином содержит значение приватности.

1. Одновременно для обеспечения атрибута с нулевым разглашением случайные значения для строк должны быть добавлены к полиному траектории, который определяется верификатором и доказывающим после согласования.

1. CRS не требуется в качестве третьей стороны на протяжении всего процесса.

1. Весь процесс не зависит от каких-либо математических задач.

Приложение

1. Официальное краткое введение в FRI

1. [Документ FRI] (https://eccc.weizmann.ac.il/report/2017/134/)

1. [Документ DEEP-FRI] (chrome-extension://cdonnmffkdaoajfknoeeecmchibpmkmg/assets/pdf/web/viewer.html?file=https%3A%2F%2Farxiv.org%2Fpdf%2F1903.12243.pdf)

1. [Рид-Соломен WIKI] (https://en.wikipedia.org/wiki/R)