Радиальные базисные функции: типы, преимущества и варианты использования

25 января 2023 г.

Это вводная статья, объясняющая основную интуицию, математическую идею & объем радиальных базисных функций при разработке прогнозирующих моделей машинного обучения.

Содержание

1. Введение
2. Основные сведения о радиальной базисной функции
3. Типы радиальной базовой функции
4. Концепция сети RBF
5. Область применения Преимущества РБФ
6. Заключение
7. Ссылки

Введение

В машинном обучении решение задач на основе алгоритмов гиперплоскости сильно зависит от распределения точек данных в пространстве. Однако известно, что реальные данные редко соответствуют теоретическим предположениям.

Существует множество функций преобразования, которые могут преобразовывать естественную форму точек данных в теоретически рекомендуемые распределения, сохраняющие скрытые закономерности данных. Radial Basis — одна из таких известных функций, которая обсуждается во многих учебниках по машинному обучению. В этой статье мы познакомимся с базовой интуицией, типами и использованием функции радиального базиса.

Основная интуиция радиальной базисной функции

Функция радиального базиса – это математическая функция, которая принимает входные данные с действительным знаком и выводит действительный результат на основе расстояния между входным значением, спроецированным в пространстве, от воображаемой фиксированной точки, расположенной в другом месте.

Эта функция широко используется во многих алгоритмах машинного обучения и глубокого обучения, таких как машины опорных векторов, искусственные нейронные сети и т. д.

Давайте разберемся с концепцией и использованием этой математической функции.

В режиме реального времени всякий раз, когда мы решаем сложные задачи машинного обучения с помощью таких алгоритмов, как SVM, нам нужно проецировать все наши точки данных в воображаемое многомерное пространство, где каждая функция будет измерением.

Предположим, у нас есть задача классификации, чтобы предсказать, сдаст или не сдаст студент экзамен.

У нас есть следующие функции в качестве независимых переменных:

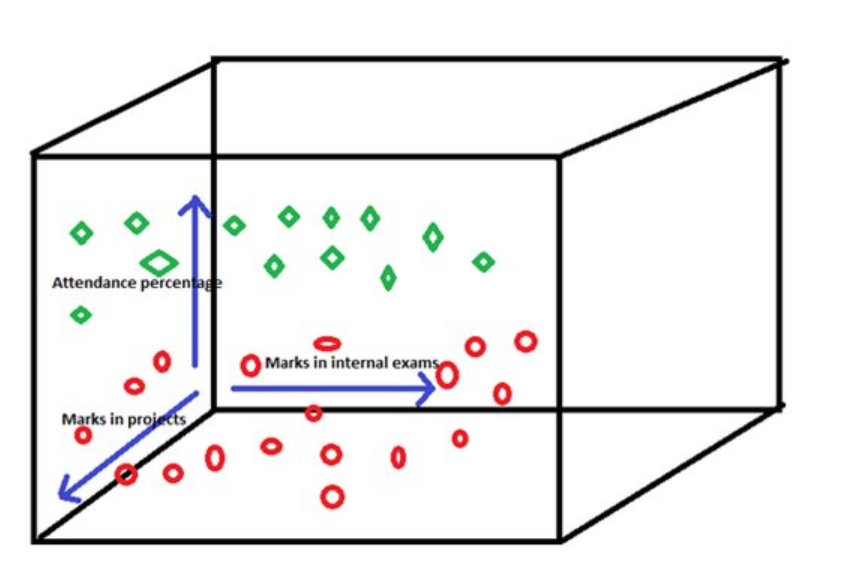
* Оценки на внутренних экзаменах * Отметки в проектах * Процент посещаемости

Итак, эти 3 независимые переменные становятся 3-мя измерениями такого пространства-

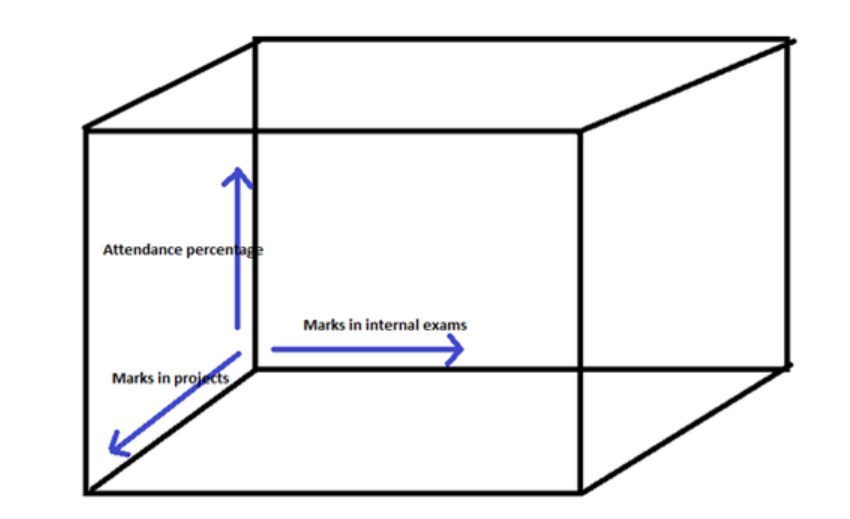
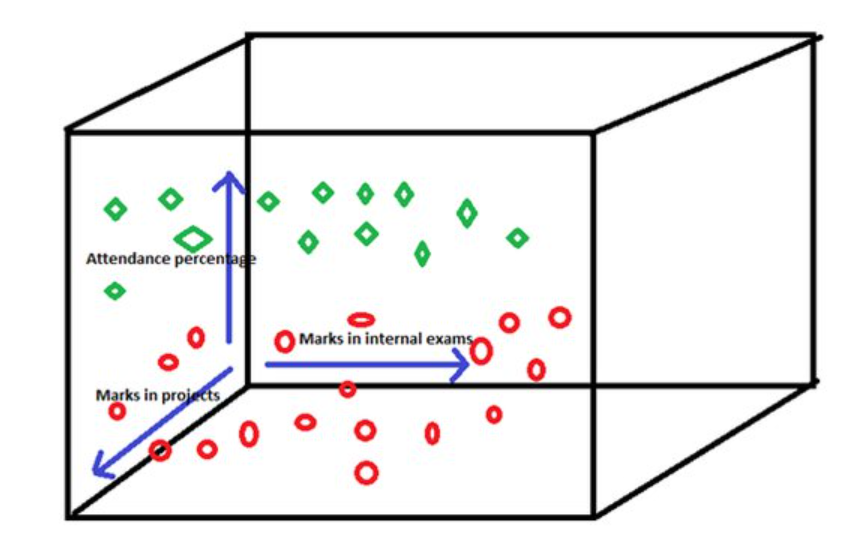
Предположим, что наши точки данных выглядят так, где-

• Зеленым цветом отмечены учащиеся, сдавшие экзамен.
• Красным цветом отмечены учащиеся, не сдавшие экзамен.

Теперь SVM создаст гиперплоскость, которая проходит через эти 3 измерения, чтобы различать неуспешных и неуспешных студентов- n n

Итак, технически теперь модель понимает, что все точки данных, попадающие на одну сторону гиперплоскости, принадлежат сдавшим экзамены студентам, и наоборот.

В нашем примере было легко создать гиперплоскость, потому что линейной и прямой гиперплоскости было достаточно, чтобы различить две категории. Но в сложных проектах реального времени эти отношения могут нарушаться во многих сценариях. Особенно когда у вас есть сотни независимых переменных, нет возможности получить линейную зависимость между точками данных, так что будет сложно создать оптимальную гиперплоскость.

В таких сценариях исследователи обычно применяют радиальную базисную функцию к каждой из точек данных, чтобы они могли провести линейную гиперплоскость через точки данных, чтобы легко решить проблему.

Учтите, что наши точки данных выглядят так в пространстве-

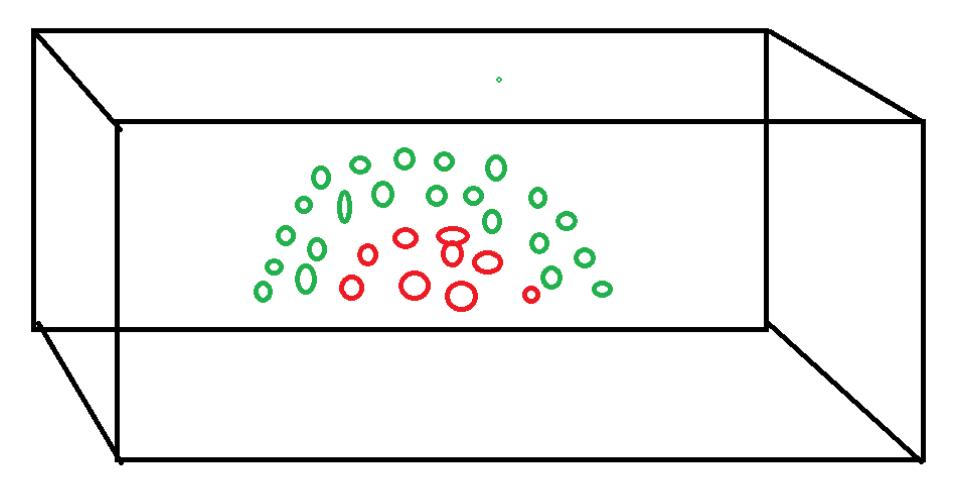
Понятно, что мы не можем использовать линейную гиперплоскость, чтобы она могла группировать точки данных в соответствии с их классами.

RBF поможет нам в таких случаях.

Некоторые исследователи обычно проецируют эти точки данных в гораздо более высоких измерениях, так что расстояние между точками данных будет увеличиваться, чтобы они могли применить некоторую функцию (RBF или любую другую функцию) для построения гиперплоскости. Но нет необходимости строить большие размеры, так как это всегда решение статистика/исследователя, который понимает закономерности в данных.

Далее мы должны отметить воображаемую точку в пространстве, где нам нужно.

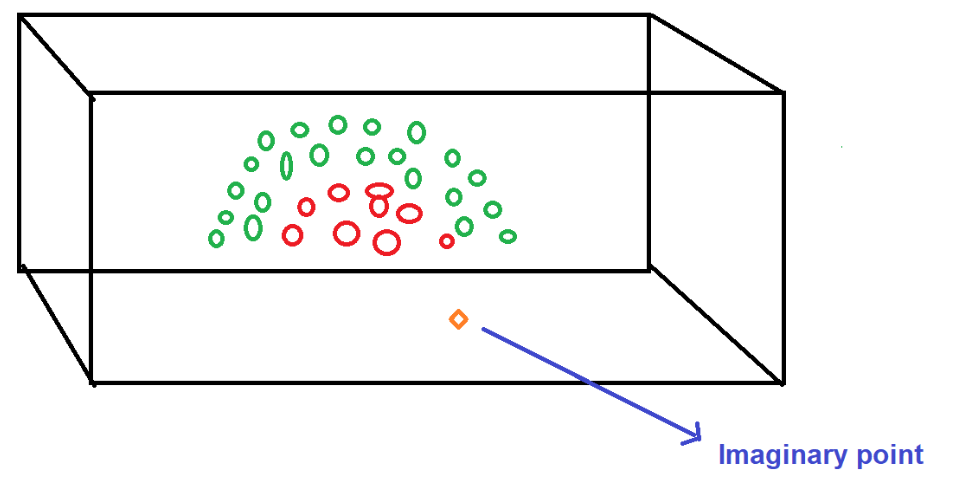
После этого нам нужно нарисовать несколько концентрических окружностей на основе этой воображаемой точки.

n 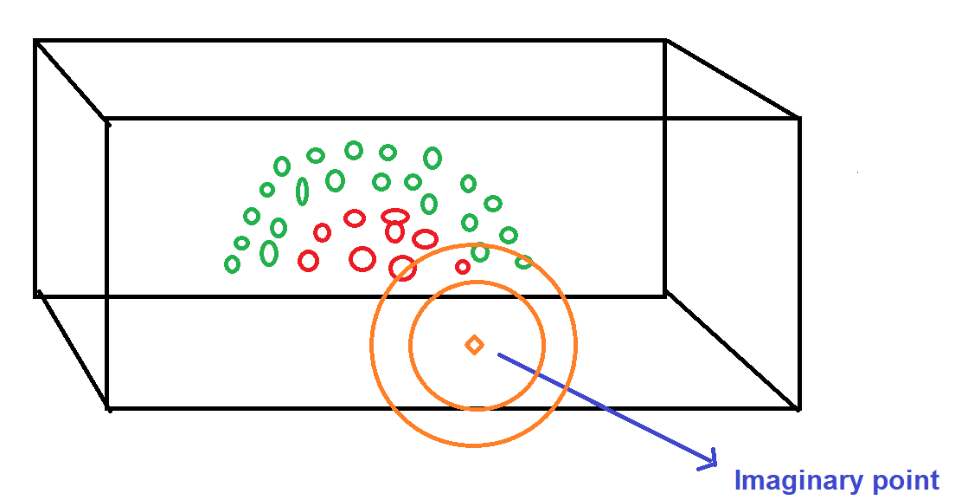n Расстояние между центром и любой точкой данных расположенный на границе круга, называется радиусом. n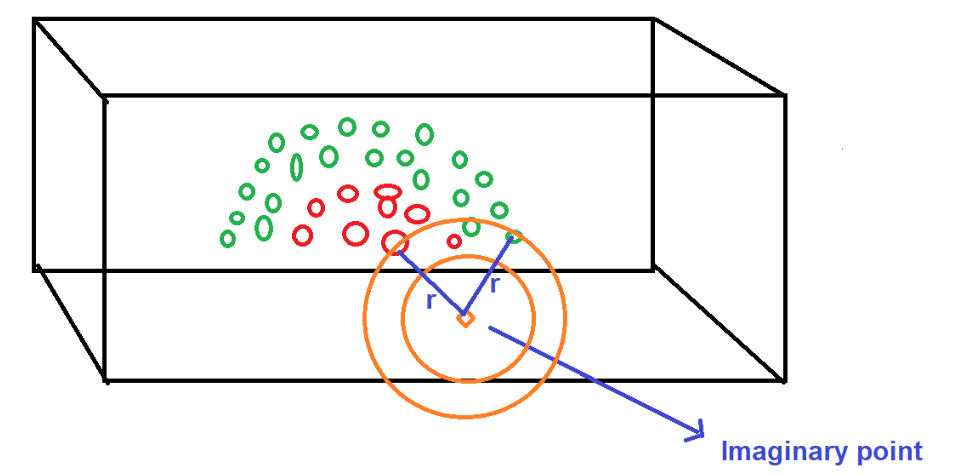

После расчета радиуса нам нужно передать это значение в математическую функцию (RBF), которая вернет реальное значение. Возвращаемое значение будет преобразованной величиной конкретной точки данных, используемой для дальнейших действий.

Типы функций радиального базиса

Существует несколько типов радиальных базисных функций. Каждый из них будет преобразовывать входное значение по-разному. Некоторые из них-

Многоквадратичная функция радиального базиса

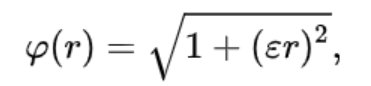
Где

• r — радиус
• ε – константа

Функция будет выглядеть следующим образом относительно времени,

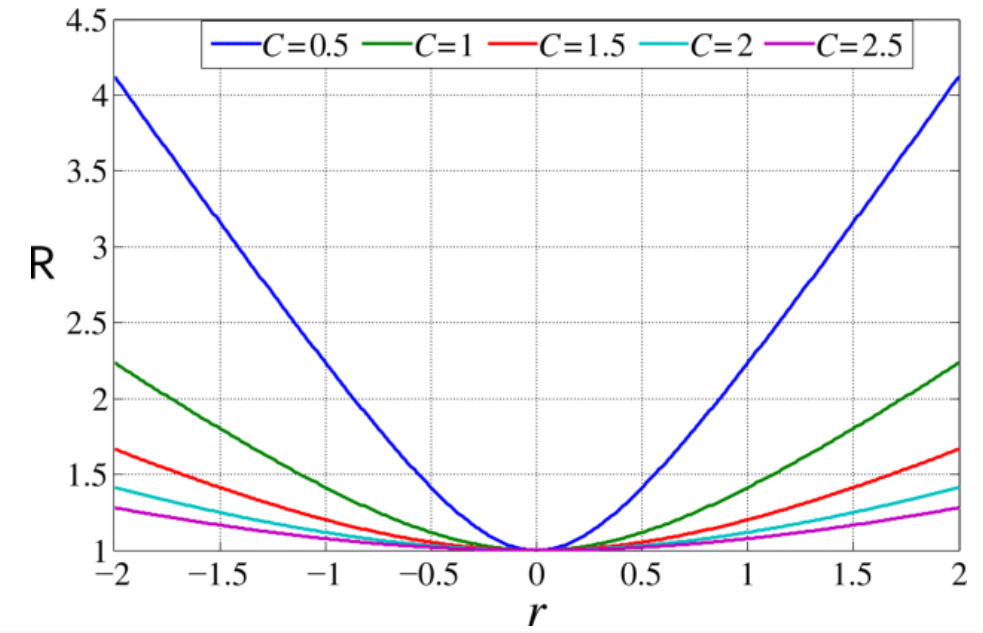
Обратная мультиквадратная функция радиального базиса

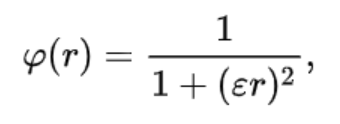
Где

• r — радиус
• ε – константа

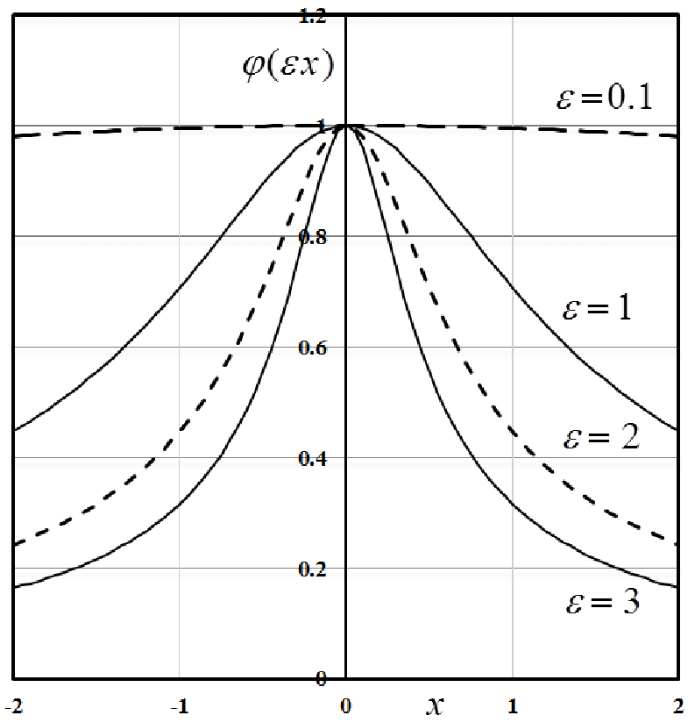
Гауссова радиальная базисная функция

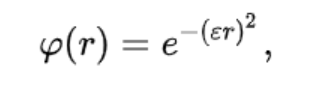Где,

• r — радиус
• ε – константа

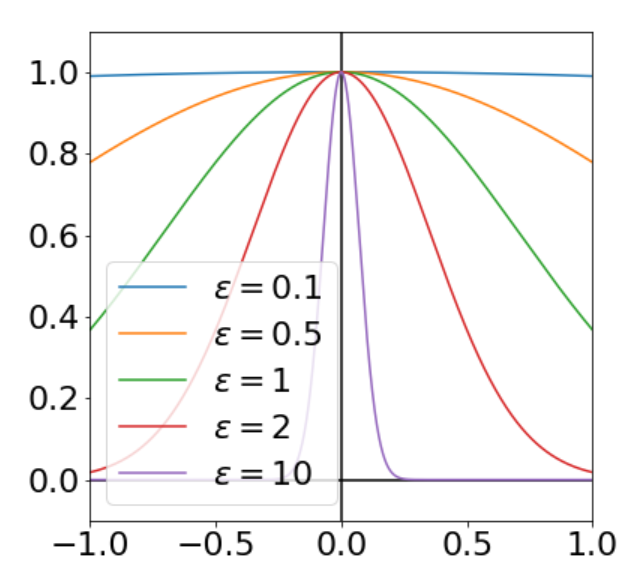
Я объясню интуитивно, что эти функции будут делать интуитивно в пространстве. Эти функции выполняют 2 разных процесса:

* Расширение точек данных по горизонтали * Сжатие точек данных по вертикали

Процесс расширения визуально будет выглядеть примерно так-

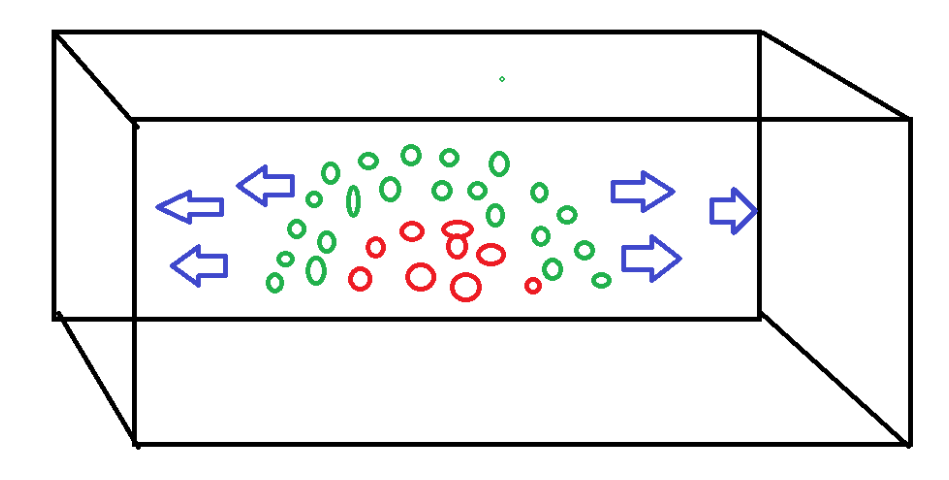
Процесс сжатия визуально будет выглядеть примерно так-

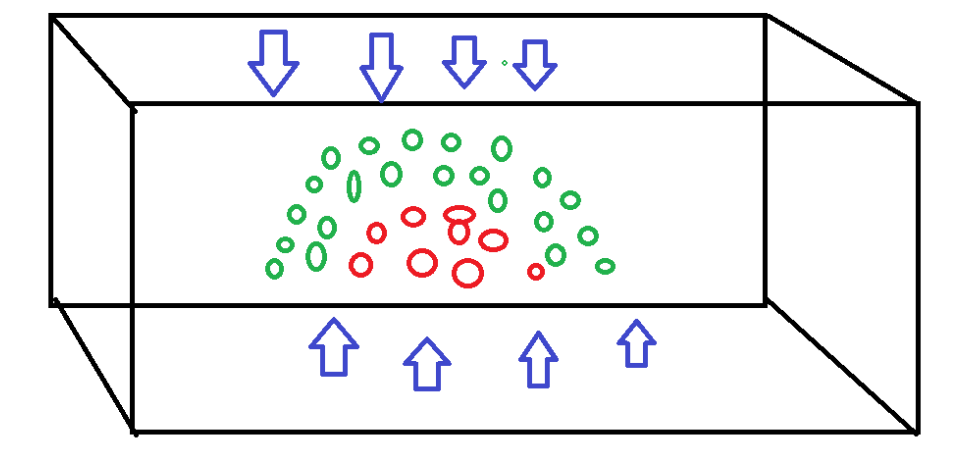
После расширения и сжатия точки данных были бы преобразованы следующим образом:

Теперь мы можем легко построить линейную гиперплоскость, которая может классифицировать точки данных следующим образом: .png"/>

Концепция сети RBF

Иногда RBF также используется вместе с искусственными нейронными сетями с одним скрытым слоем. В сетях такого типа в качестве функций активации в скрытых слоях будут использоваться RBF. Помимо скрытого слоя, будет входной слой, который содержит несколько нейронов, где каждый из них представляет переменную признака, а выходной слой будет иметь взвешенную сумму выходов из скрытого слоя для формирования выходных данных сети.

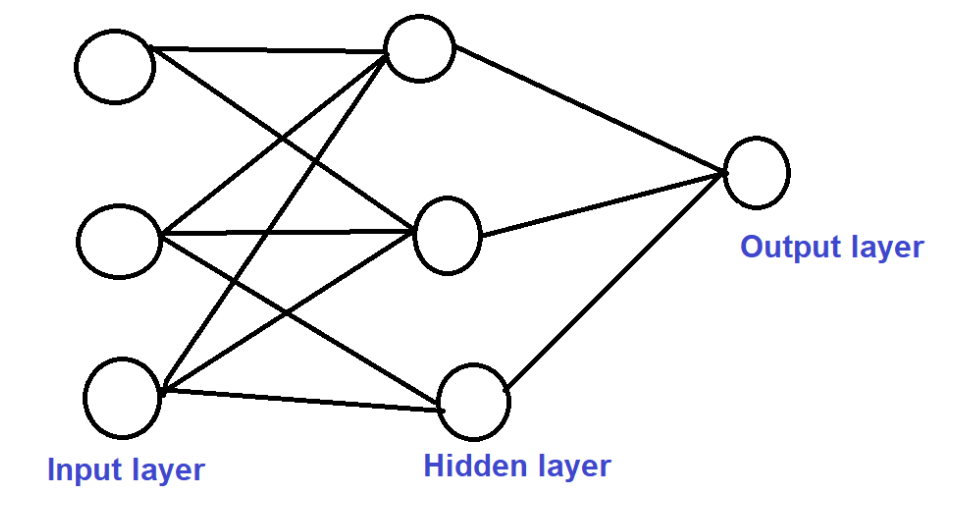
Такие сети называются сетями RBF.

Область действия и охват Преимущества РБФ

• С помощью функции RBF можно решить проблемы с наборами данных со сложными нелинейными распределениями.
• Функция RBF имеет высокую устойчивость к входному шуму.
• В нейронной сети RBF будет только один скрытый слой, с которым очень легко работать.
• Скрытые закономерности в распределении можно лучше обобщить после применения функции RBF.
• В нейронной сети RBF мы можем легко интерпретировать значение/функцию каждого узла в скрытом слое RBNN. Это сложно в многоуровневом восприятии.
• Некоторые из гиперпараметров многослойного персептрона, такие как количество узлов в скрытом слое, количество скрытых слоев и т. д., трудно оптимизировать. Но их нет в нейронных сетях RBF.

Заключение

В этой статье мы обсудили одну из самых полезных функций преобразования в машинном обучении. Я попытался объяснить эту сложную концепцию без глубоких математических расчетов в понятной форме, ориентированной на новичков в пространстве обучения AIML.

Эта функция доступна в виде встроенной библиотеки в большинстве языков программирования, ориентированных на науку о данных, таких как Python или R. Следовательно, ее легко реализовать, если вы понимаете теоретическую интуицию. Я добавил ссылки на некоторые дополнительные материалы в раздел ссылок, где вы можете углубиться в сложные расчеты, если вам это интересно.

Ссылки

1. Радиальные базисные функции — Википедия
2. Сети с радиальной базисной функцией Архивировано 23 апреля 2014 г. по адресу Wayback Machine
3. Брумхед, Дэвид Х.; Лоу, Дэвид (1988). "Многопараметрическая функциональная интерполяция и адаптивные сети" (PDF). Сложные системы. 2: 321–355. Архивировано из оригинала (PDF) от 14 июля 2014 г.
4. Майкл Дж. Д. Пауэлл (1977). «Перезапустите процедуры для метода сопряженных градиентов». Математическое программирование. 12 (1): 241–254. doi:10.1007/bf01593790 . S2CID 9500591< /а>.
5. Шахин, Ферат (1997). Подход к задаче классификации цветных изображений в промышленном приложении реального времени ( Магистр наук). Технологический институт Вирджинии. п. 26. hdl:10919/36847. Радиальные базисные функции были впервые введены Пауэллом для решения реальной задачи многомерной интерполяции.

---

Оригинал