Оптимизация алгоритма мультискалярного умножения: технический обзор Sin7Y (21)
blockchain good-company blockchain-technology sin7y algorithms optimization multi-scalar-multiplication endomorphism

Оптимизация алгоритма мультискалярного умножения: технический обзор Sin7Y (21)

16 апреля 2022 г.

Пусть G – циклическая группа, P_i ∈ G – элемент группы, a_i ∈ Z  – скаляр, а мультискалярное умножение (MSM ) — это алгоритм вычисления ∑_{i=1}^{n} a_{i} P_{i} , суммы нескольких скалярных умножений. Поскольку групповая операция сложнее, чем сложение и умножение элементов в конечном поле, алгоритм MSM используется для максимально возможного сокращения количества групповых операций. Обычно G является циклической группой, определенной на эллиптической кривой y^2=x^3+ax+b на конечном поле F_p, с порядок |G|* b ≈ 256 бит, а 0 ≤ a_i< 2^b. Если групповая операция проводится по простому алгоритму быстрого возведения в степень, количество групповых операций, необходимых для каждого a_i.P_i, составляет в среднем 1,5 млрд раз, а для всех a_i.P_i — 1,5b раза. Далее мы представим некоторые методы оптимизации, соответствующие большему n***.


Оптимизация на основе оконной техники


Мы можем разделить b битовый скаляр на окна ширины c: уменьшить скаляр до 2^c базовой системы.



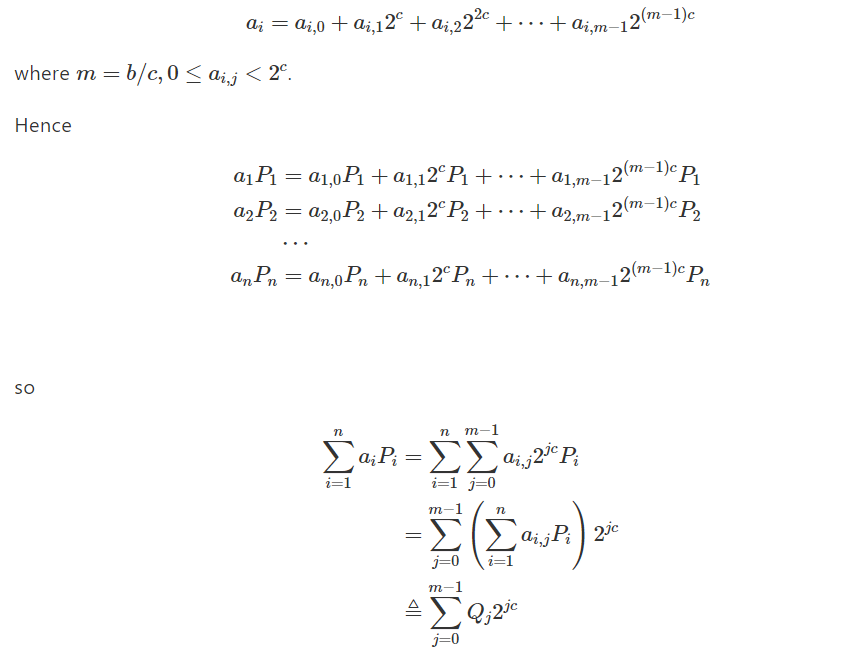
Здесь Q_j=∑_{i=1}^{n} a_{i j} P_{i}, поэтому мы уменьшаем исходную проблему алгоритма b- превратил MSM в меньшую c-битную проблему. Мы можем поместить те же скаляры из ∑_{i=1}^{n} a_{i j} P_{i} в ведро и записать их в другой форме:



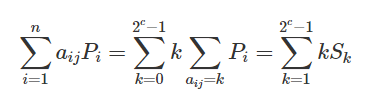
Например, когда c = 3, оно рассчитывается как:



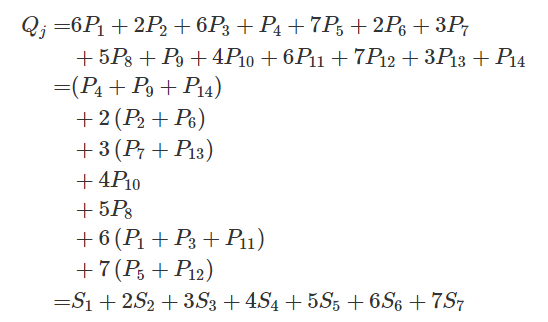
При расчете ∑kS_k установите частичную сумму T_l=S_l+⋯+S_k, затем



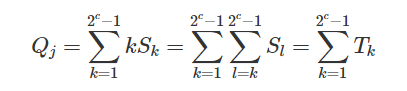
Однако результаты операции T_l можно получить с помощью повторяющейся последовательности T_l=T_l+1+S_l. Это означает, что для операции для каждого T_l требуется только одна групповая операция. В алгоритме MSM со скаляром cc-bit все S_k требуют n−2^c+1 раз групповой операции. Все T_k требуют 2^c-1* раз, а сумма этих T_k требует 2^c-2 раз групповой операции. Следовательно, для каждого окна со значением c требуется n+2^c−2 раз групповых операций. Операция ∑{j=0}^{b / c-1} Q{j} 2^{j c} требует только обычного метода быстрого возведения в степень на (b/c−1 )(c+1)=b − c + b/c−1* раз групповой операции.


Подводя итог, мы можем сделать вывод, что общее количество групповых операций, требуемых методом оконной техники шириной c, равно



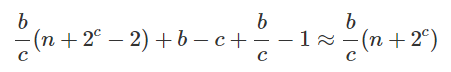
Установите c = logn, тогда число групповых операций составит 2 млрд/logn. Когда n≈10^5 , количество групповых операций уменьшается до 1/12 от исходного значения.


Оптимизация на основе группового эндоморфизма


Для циклической группы G на эллиптической кривой y^2=x^3+ax+b на конечном поле F_p, если можно найти следующий групповой эндоморфизм φ: существует * α,β ∈ F_p, удовлетворяющие условию φ(x,y)=(αx,βy) для всех точек на G, то легко доказать, что такой эндоморфизм является отображением умножения, а именно существует λ , делающее φ(P)=λP выполненным для всех точек P на G, что означает, что всякий раз, когда нам известны координаты одной точки, мы можем изменить их на координаты другой точки, просто умножив число в F_p* на оба значения абсциссы и ординаты. Алгоритм может быть дополнительно оптимизирован на основе этого важного свойства.


Когда λ = −1, α = 1, β = −1. Обратное значение одной точки можно получить, только отняв от ординаты противоположное число. Основываясь на этой особенности, в простом алгоритме быстрого возведения в степень скаляр может быть записан в несмежной форме (NAF), а именно ∑e_{i}.2^{i}, e_{i} ∈ { −1,0,1} и любые два соседних e_i не могут быть ненулевыми одновременно. По сравнению с b-битными скалярами число групповых операций в алгоритме быстрого возведения в степень может быть уменьшено с исходного среднего значения 3/2⋅b раз до 4/3⋅b раз. . Эту технику также можно использовать для оптимизации оконной техники. После записи a_i в a_i=∑{j=0}^{b / c-1} a{i, j} 2^{j c}, 0 <= a_{i, j}<2 ^{с}


провести следующую операцию:


Результат a_i=∑{j=0}^{b / c-1} a'{i, j}^2^{j c} и -2^{c-1} < = a'_{i, j}^ <= 2^{c-1} можно получить. Поскольку сложность сложения и вычитания в групповой операции эллиптической кривой одинакова, мы можем поместить эти члены в корзину в соответствии с абсолютным значением скаляров. Таким образом, количество групп может быть уменьшено с исходных 2c до 2^c , а общее количество необходимых групповых операций уменьшено с (1) до:



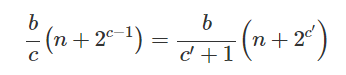
Если параметры эллиптической кривой особые, например, кривую BLS можно записать как y^2=x^3+b, а p ≡ 1(mod3), взять третий элемент -порядка α из F_p^x, то существует соответствующий λ который содержит λ(x,y)=(αx,y)



Алгоритм 1: цифры со знаком


Кроме того, λ3 ≡ 1(mod |G| ). Тогда операцию умножения можно оптимизировать следующим образом:



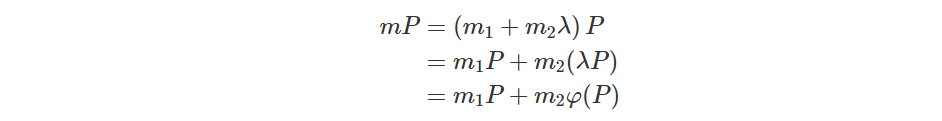
Из [1] мы можем найти достаточно малый скаляр |m1|, |m2|<√G , чтобы сделать приведенное выше уравнение верным, что дает нам способ уменьшить умножение битов bb на умножение двух битов b/2. Используйте его в Windowing Technique, и количество групповых операций сократится до



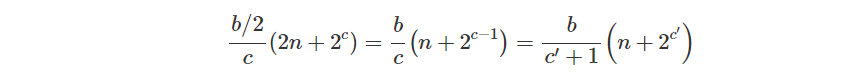
Таким образом, оба вышеупомянутых метода оптимизации могут сократить количество групповых операций на 5,5% при n=10^5.


Рекомендации


[1] Франческо Сика, Матье Сье и Жан-Жак Кискватер. Анализ метода Галланта-Ламберта-Ванстона, основанного на эффективных эндоморфизмах: эллиптические и гиперэллиптические кривые. В Международном семинаре по отдельным областям криптографии, страницы 21–36. Спрингер, 2002.


Оригинал

Recent Post

Categories

PREVIOUS ARTICLE
NEXT ARTICLE