WriteUp — Фантастические таблицы умножения

… и как их рисовать

С возвращением! Сегодня мы немного отойдем от обычных проблем с кодированием, чтобы взглянуть на то, с чем я играл, когда начал учиться программировать. На самом деле это немного глуповатая игра, но также это прекрасная возможность изучить математику с таблицами умножения, программирование и… черепах!

Готовый? Тогда начнем.

Таблицы умножения

Таблица умножения, вероятно, является первым понятием, которое все учат в начальной школе после базовой арифметики. Я до сих пор помню метод своей учительницы: она нас учила, запоминая, а потом мы устраивали небольшие соревнования в классе. Нам дали лист бумаги с таблицей и некоторыми отсутствующими результатами, и мы должны были заполнить все таблицы умножения, выученные до этого момента: тот, кто финишировал первым, получил приз. Когда-то это было очень забавно.

Однако, помимо того, что это инструмент для повседневной жизни и школьных упражнений, если мы присмотримся к таблицам умножения, мы обнаружим, что за ними скрыто намного больше.

Например: что произойдет, если мы попытаемся их нарисовать?

Рисование таблиц

Идея этой небольшой программы пришла мне в голову после просмотра видеоролика профессора Полстера, который ведет великолепный канал YouTube Mathologer. Вы можете ознакомиться с его содержанием здесь: он гораздо глубже углубляется в концепцию, говоря о множествах Мандельброта и Z-функции Римана, и он слишком хорошо объясняет эти понятия в веселой и легкой для понимания форме.

Мы ограничим нашу игру жесткими изображениями таблиц умножения, специально написав некоторый код, который будет рисовать их для нас.

Идея довольно проста: сначала рисуем окружность, а затем нумеруем несколько точек на окружности, оставляя между ними одинаковое расстояние. После этого начинаем вычислять результаты для заданной таблицы умножения и соединяем результаты. Например, для таблицы умножения на 6:

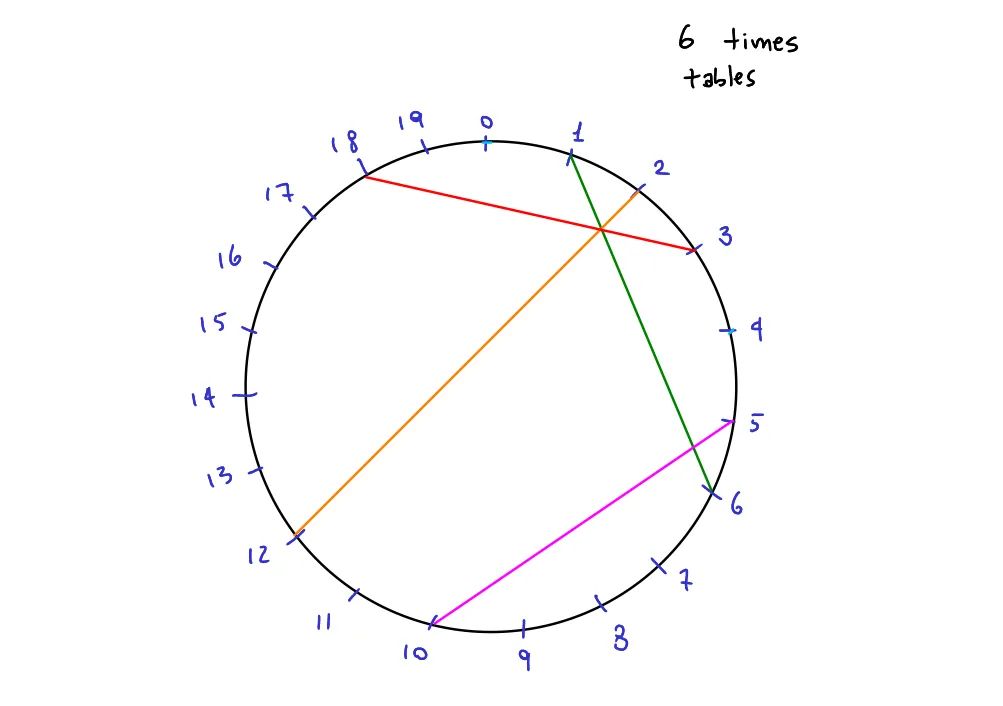
и так далее. Что произойдет, если мы соединим большее количество точек? Давайте узнаем.

Быстрое обновление

Прежде чем начать, кратко ознакомьтесь с концепциями, которые мы здесь увидим. Окружность – это набор точек, равноудаленных от ее центра, также называемых началом (O). Это расстояние называется радиусом (r).

На плоскости, предполагая, что у нас есть исходная точка O с координатами x и y, мы можем найти координаты точки A на окружности со следующими уравнениями:

где θ – угол, создаваемый точкой A, началом координат и осью y плоскости, скорректированный с помощью координат x и y. Например, в этом круге O в (4,4) и r = 3. Точка A начерчена на его окружности, образуя угол a 30°. Мы можем вычислить координаты A как

Вы можете убедиться в этом на рисунке ниже.

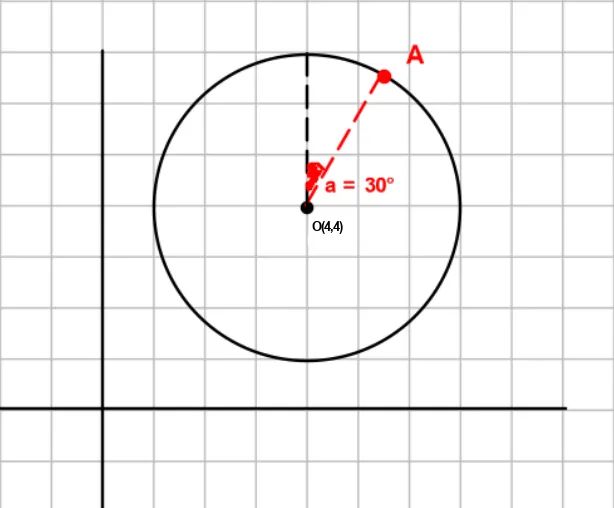
Еще одним важным понятием является разница между градусами и радианами:

• Градус (°) — это единица измерения углов, относящихся к полному обороту окружности. Например, зная, что полный оборот равен 360°, мы заключаем, что половина площади круга должна составлять угол 180°;
• Радиан (Rad) также является единицей измерения углов, но относится к длине полукруга от одной точки до другой на окружности. По сути, это расстояние, пройденное по окружности, и угол, создаваемый начальной и конечной точками.

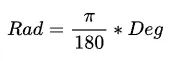
Не вдаваясь слишком глубоко, мы можем рассчитать Rad по следующему уравнению:

Мы также воспользуемся модульной арифметикой для вычисления результатов на окружности. Проще говоря, оператор по модулю дает нам остаток от деления: например, A%B = C (красный, поскольку «A по модулю B равно C») будет означать, что остаток от A/B равно С.

Это достаточно информации для нашей сегодняшней миссии. Ниже мы будем широко использовать эти концепции, поэтому внимательно их ознакомьтесь.

Теперь самое интересное, давайте начнем рисовать!

Черепаха

Когда я начал изучать Python, я много играл с этой библиотекой, turtle, которая это отличный инструмент для рисования форм и геометрии. Его часто пропускают при изучении языка, главным образом потому, что он не имеет реальной цели и его использование очень ограничено. Однако я думаю, что это отличная библиотека, хорошо документированная и простая в использовании, которая действительно достойна изучения и развлечения.

Библиотека очень проста: мы создадим черепаху (которую мы назовем Бобом, как ее часто называют в обучающих материалах в Интернете), представленную стрелкой на экране, и будем двигать ее, задавая направления и точки поворота. Вот пример некоторых основных команд:

import turtle

bob = turtle.Turtle()

bob.fd(50)          # Go 50 pts forwars
bob.left(90)        # Turn 90° left
bob.back(50)        # Go 50 pts backwards
bob.right(90)       # Turn 90° right

bob.pensize(2)          # Change line size
bob.pencolor("red")     # Change line color

bob.fd(50)
bob.left(90)
bob.fd(100)

bob.pensize(3)
bob.pencolor("green")
bob.left(90)
bob.fd(100)

turtle.mainloop()

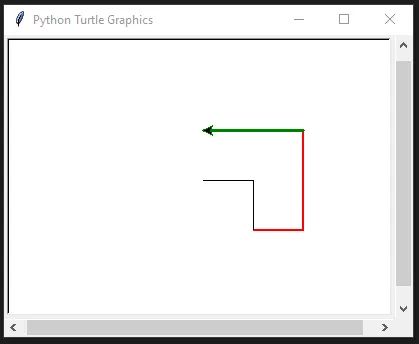
Тогда давайте начнем рисовать!

Круг

https://gist.github.com/NicolaM94/5b6dd5e1516ed9c9105bee2df2576e67?embedable= правда #file-circle-py

Сначала мы определяем функцию drawCircle, которая принимает следующие параметры:

* turtle, черепаха, которую мы двигаем; * radius, радиус окружности; * origin, начало круга, заданное как кортеж координат x и y, по умолчанию установленное на (0,0); * penSize, penColor и writeLabel, которые являются графическими параметрами для установки ширины линии, цвета и метки в начале координат

Обратите внимание, что черепашка начинает рисовать с самой нижней точки окружности, поэтому функция просто перемещает черепаху вниз на длину радиуса, рисует круг, а затем снова перемещается вверх на радиус.

Добавление точек

Сначала нам нужно решить, сколько точек добавить в окружность. Начнем с простого и попробуем с 12, как на часах! Нам нужно нанести на окружность 12 точек на одинаковом расстоянии друг от друга.

Зная, что угол полного кругового вращения равен 360°, мы можем просто разделить это вращение на 12 частей и получить угол 360°/12 = 30° для каждой точки. Кроме того, мы будем работать с math.sin и math.cos из библиотеки Python math, в которой в качестве меры используются радианы, поэтому лучше конвертировать наш угол прямо сейчас. Давайте напишем функцию, которая завершит это:

https://gist.github.com/NicolaM94/59e4243ed6171020eb81f86168d9b16e?embedable =правда #file-angle-py

А теперь расставим точки на окружности:

https://gist.github.com/NicolaM94/c7031addaa3371dfc673ce988220a495?embedable =правда #file-drawpoints-py

Мы определяем функцию drawCircumferencePoints , которая принимает обычные параметры и новый, coordinates , который представляет собой словарь для сбора точек и их координат. Таким образом, мы можем избежать пересчета всех точек на следующем шаге, что очень удобно при работе с большим количеством точек.

Внутренняя функция singlePointDraw просто перемещает черепашку в координаты для заданного угла и ставит точку.

С помощью этой функции мы перемещаемся по нашим точкам и отбрасываем точку с помощью singlePointDraw : угол всегда будет равен 30°, поэтому для каждой точки в диапазоне мы отбрасываем точку в i*angle< /code> : для точки 0 мы поместим ее в 0*30° = 0° , для точки 1 в 1*30° = 30° , для точки 2 при 2*30° = 60° и т. д.

На этом этапе мы также собираем положение нашей черепахи и угол в словаре coordinates. Собирать ракурс особо не нужно: я использовал его для проверки и оставил там (непреднамеренно ;D)!

Наконец, если для параметра writeLabel установлено значение True , мы будем писать номер точки рядом с каждой точкой.

При вызове drawCircle и drawCircumferencePoints у вас должно получиться что-то вроде этого:

Также обратите внимание, что точки начинаются с 0 и заканчиваются на 11: вот почему модульная арифметика скоро придет на помощь.

Расписания!

Наконец-то запишем нашу таблицу умножения! Возьмем, к примеру, число 3 и нарисуем его расписание.

https://gist.github.com/NicolaM94/f3ca34063ff9a8917290fdb4fd56f083?embed способный = истинный #file-drawtable-py

Для этого мы определяем другую функцию, drawTable . После этого мы вычисляем базовый угол, чтобы иметь ссылку в этой функции, и сохраняем его в переменной angle.

Затем мы начинаем перебирать наши точки. Для каждой точки мы определяем:

* начальная точка, взятая из координат, которые мы указали ранее; * конечная точка, рассчитанная как значение начальной точки, умноженное на выбранную таблицу умножения.

Здесь вступает в действие оператор по модулю: умножение, например, 3 * 11 дает в результате 33, поэтому мы должны перейти к точке 33 на окружности. Однако у нас есть только 12 точек на окружности, поэтому мы можем использовать модуль для вычисления 33%12 = 9, что является именно той точкой, в которой мы закончим, если обойдем круг 33 раза.

Наконец, мы просто рисуем линию между начальной и конечной точками и снова начинаем цикл со следующего числа.

На этом этапе у вас должно получиться что-то вроде этого:

Подведение итогов

Давайте объединим весь код в одну функцию:

https://gist.github.com/NicolaM94/4124e8e1b60a806dfa8e18d34f5f1 611?встраиваемый=истина #file-timetablesdrawer-py

Эта функция в основном вызывает другую функцию, созданную выше, в правильном порядке, не более того. Он добавляет параметр speed для установки скорости черепахи, поэтому мы можем контролировать скорость анимации (попытка с большим количеством точек занимает немного времени!). Он также содержит переменную coordinates , которая раньше находилась вне функции drawCircle, а теперь содержится во внешней функцииtimesTablesDrawer.

Еще несколько баллов, пожалуйста?

Изображение, полученное с номером 3, было нормальным, но не шедевром: это был просто набор линий внутри круга. Это потому, что на окружности слишком мало точек. Давайте попробуем добавить еще: например, 200 баллов!

Так милее! Как странно нарисована фигура, правда?

Эти типы кривых называются кардиоидами, поскольку их форма напоминает сердце. Это довольно ясно, если вы посмотрите на изображение на обложке, которое представляет собой кардиоидную таблицу с умножением на 2. Вообще говоря, такие формы имеют количество «выпуклостей», равное выбранной таблице умножения минус один: в этом примере таблица времени была 3, а на самом деле на изображении есть 2 круглых выпуклых формы.

Эти кардиоиды появляются повсюду вокруг математики, физики, химии и природы. Например, в микрофоны и яблоки… а также в чашку чая!

И это еще не все! Если мы попытаемся нарисовать более высокие таблицы умножения, мы увидим множество различных форм: некоторые из них не имеют ничего общего с кардиоидами, например таблица умножения 99 или 66!

Вот несколько примеров с большими числами:

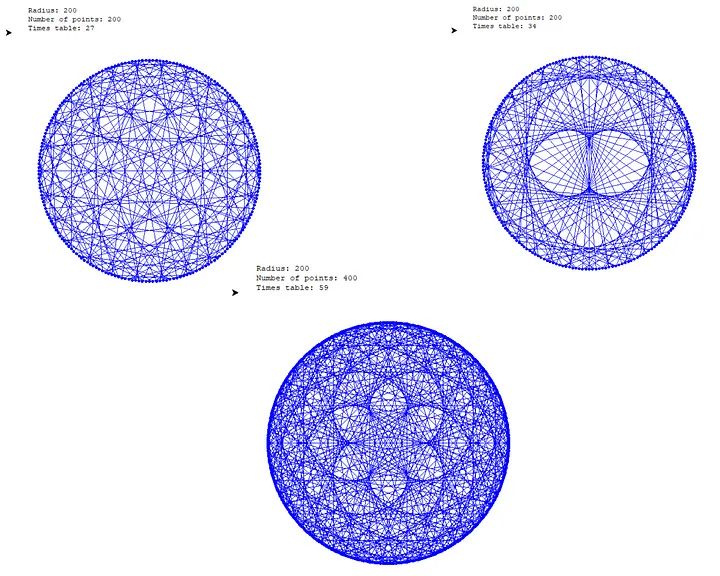
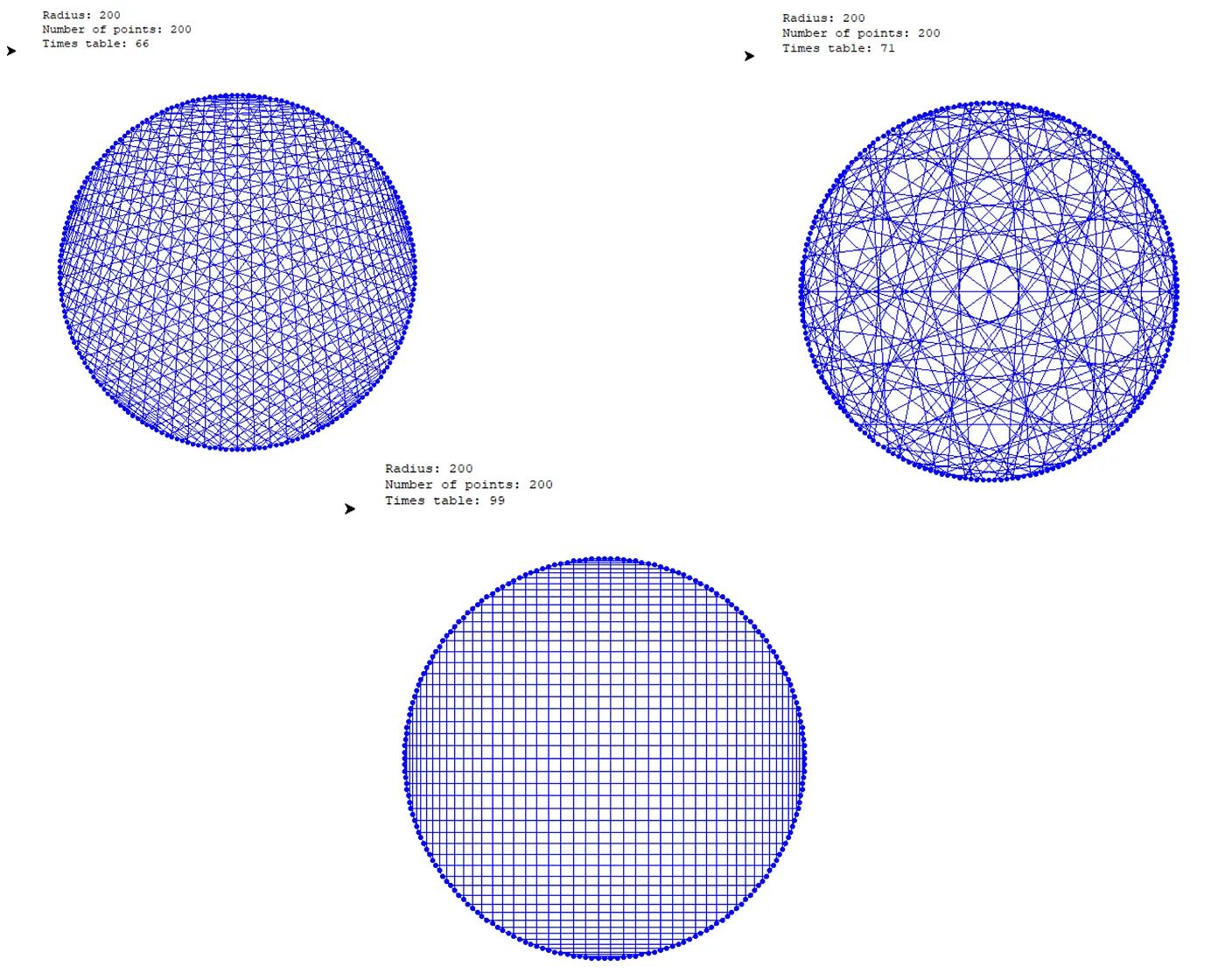
Попробуйте с разным количеством очков и таблицами умножения: уверяю вас, очень весело смотреть, как маленькая черепашка бегает и рисует красивые фигуры!

Промежуточные результаты

Мы также можем вывести промежуточные результаты, то есть таблицы умножения с десятичными знаками. Также очень здорово видеть промежуточные результаты, потому что это дает нам представление о том, как изображение создается и меняется от одного результата к другому. Вот анимация таблицы умножения со 2 на 3 (извините за плохое качество!):

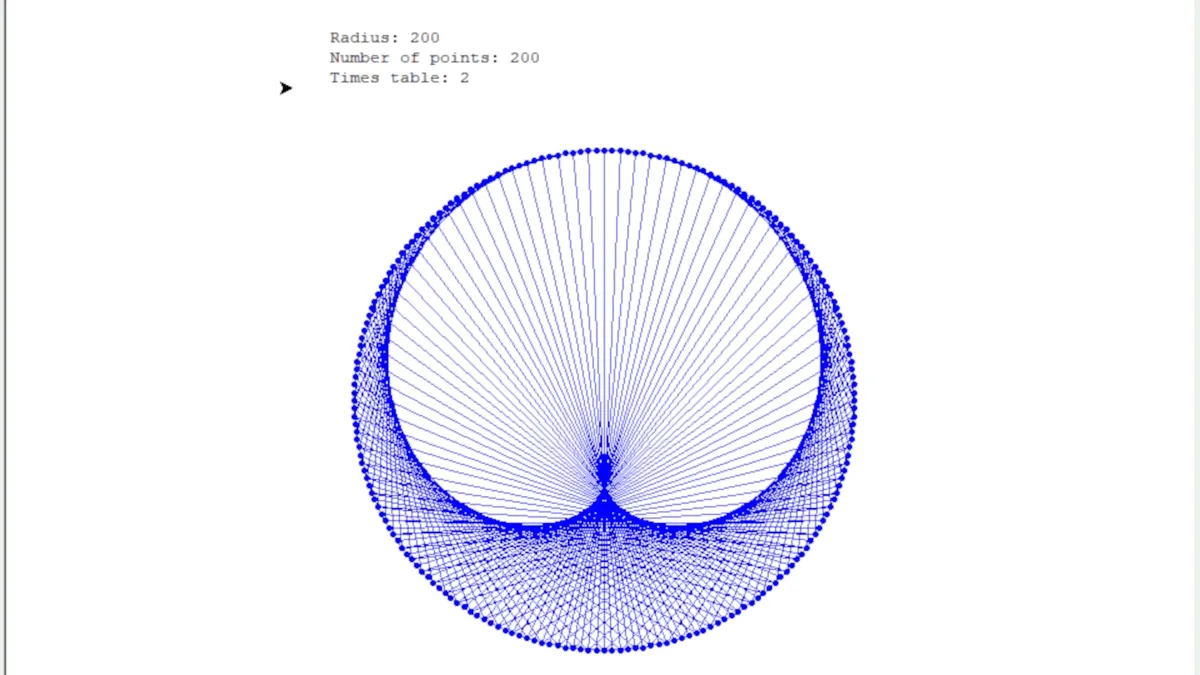
Вы можете видеть, как форма в основном продолжает вращаться и огибаться сама по себе, почти смещаясь влево, чтобы создать следующую кардиоиду. Как здорово!

Выводы

Вот оно! Долгий путь (как и в большинстве случаев здесь). Это немного отличается от обычных статей о решении проблем с кодированием, но недавно я снова посмотрел это видео, и мне сразу же захотелось поделиться своей попыткой.

Я также написал простую программу для рисования этих фигур, вы можете загрузить ее с моей страницы Github, здесь (нажмите "Raw", чтобы загрузить его!): не стесняйтесь использовать его в любое время и в любом месте.< /сильный>

Надеюсь, вам понравилось и было интересно! Если да, пожалуйста, похлопайте в ладоши или поделитесь этим с тем, кому это тоже может понравиться: это сделает мой день лучше!

Как всегда, спасибо за внимание.

Никола