Что такое динамическое программирование и мемоизация?

Зачем мне динамическое программирование?

Динамическое программирование — это процесс разбиения большой проблемы на более мелкие.

Используя ответы на эти более мелкие проблемы, мы можем более эффективно найти общее решение.

Мы также узнаем о термине «запоминание» и о том, как он связан с динамическим программированием.

Как работает динамическое программирование?

Типичным примером динамического программирования является последовательность Фибоначчи. Это хороший пример, поэтому мы будем использовать его и здесь.

Если вы уже знакомы с последовательностью Фибоначчи (и вычисляете ее с помощью рекурсии), то можете пропустить следующий раздел.

Если вы не уверены, что это значит, или хотите быстро освежить в памяти информацию, читайте дальше...

Последовательность Фибоначчи

Это последовательность чисел, где каждое число рассчитывается путем сложения двух предыдущих вместе:

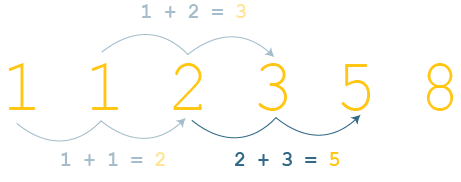
Представьте, что я прошу вас программно вычислить 6-е число в последовательности (то есть «8», как показано выше).

Как бы вы его рассчитали?

Вот некоторый код JavaScript для функции, которая делает именно это:

```javascript

функция f(n) {

// Первое и второе значения всегда равны 1

если (n == 1 || n == 2)

вернуть 1;

// Вычислить два предыдущих значения в последовательности

// используя эту же функцию

вернуть f (n - 1) + f (n - 2)

// Вычислить 6-е значение в последовательности

пусть ответ = f(6)

Это будет работать нормально, но медленно.

Вы можете видеть, что функция вызывает сама себя; это рекурсивно.

Чтобы вычислить 6-е число Фибоначчи, нам сначала нужно вычислить 4-е и 5-е числа Фибоначчи.

Затем каждый из этих должен вычислить свои предыдущие числа, и это повторяется вплоть до начала последовательности.

Вот как это выглядит, если изобразить это в виде графика.

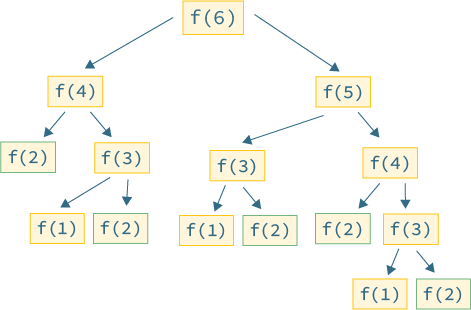
Вы можете видеть, что здесь много дублирования. Например, 2-е значение в последовательности вычисляется 5 раз!

Для небольших чисел в последовательности это не так уж плохо, но ситуация быстро ухудшается. Для более поздних чисел в последовательности это вскоре стало бы непрактичным даже на современном компьютере.

Так как нам лучше?

Динамическое программирование и запоминание

Один из способов улучшить эту функцию — сохранять результаты наших предыдущих вычислений по ходу работы.

Таким образом, нам нужно вычислить каждое число в последовательности Фибоначчи только один раз.

В этом суть динамического программирования:

Динамическое программирование разбивает большую проблему на меньшие задачи и использует эти для получения ответа.

Поскольку мы достигаем этого, сохраняя предыдущие результаты на потом, мы также используем «запоминание»:

Мемоизация сохраняет результат предыдущего вычисления, чтобы мы могли использовать его позже, чтобы сделать общий алгоритм более эффективным.

Мы могли бы реализовать эти концепции в рекурсивном подходе, описанном выше, но легче следовать, если мы используем подход «снизу вверх».

Давайте сначала посмотрим на код, а затем обсудим, почему этот алгоритм называется «восходящим»:

```javascript

функция f(n) {

// Первое и второе значения всегда равны 1

если (n == 1 || n == 2)

вернуть 1

пусть результат = 0

// Используется для хранения двух предыдущих результатов

пусть lastButOneValue = 1

пусть последнее значение = 1

// Работаем с пункта 3 последовательности (пункты 1 и 2 являются

// особый случай, см. выше), вычисляем каждое значение по очереди

for (пусть i = 3; i <= n; i++) {

// Рассчитайте это число, сложив вместе

// предыдущие два

результат = lastValue + lastButOneValue

// Обновить значения

// предыдущие два элемента в последовательности

lastButOneValue = последнее значение

последнее значение = результат

вернуть результат

// Вычислить 6-е значение в последовательности

пусть ответ = f(6)

Здесь мы вычисляем последовательность Фибоначчи по порядку — с самого начала — пока не дойдем до числа в нужной нам последовательности.

По мере продвижения мы сохраняем результаты предыдущего значения и предыдущего.

Получение следующего значения тривиально. Просто добавьте эти два вместе.

Вот снова график исходного (неэффективного) алгоритма, но мы выделили только те расчеты, которые делаем в этой новой версии:

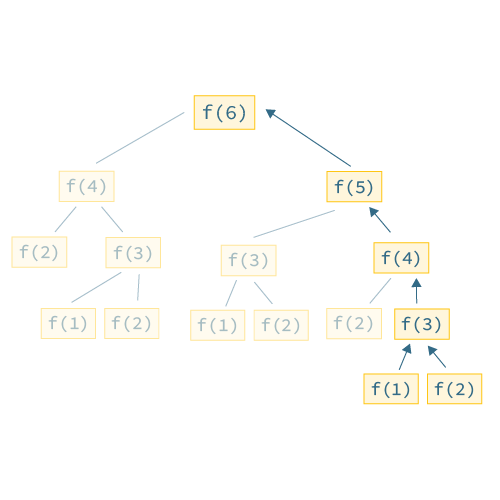
Вы можете видеть, что на этот раз, вместо того, чтобы начинать с ответа и работать в обратном направлении, мы работаем вперед, пока не достигнем нужного нам значения.

Когда мы визуализируем это, мы работаем снизу вверх на графике — отсюда подход «снизу вверх».

Этот алгоритм намного эффективнее, дублирования вообще нет!

Здесь мы узнали несколько новых терминов, так что давайте подведем итоги:

Резюме: что такое динамическое программирование?

В нашем последнем алгоритме используется динамическое программирование, потому что мы разбиваем большую проблему на меньшие проблемы и используем их результаты, чтобы получить общий ответ.

Он также использует запоминание, потому что мы сохраняем результаты предыдущего шага, чтобы избежать их повторного вычисления позже.

Это был подход «снизу вверх», потому что, когда мы визуализируем проблему в виде графика, мы работаем от основания графика вверх** (а не сверху вниз, как в менее эффективном алгоритме).

(также отправлено в информационный бюллетень BaseClass)