Что такое изолированный лес? И как он обнаруживает выбросы?

Изолирующий лес — это простой, но невероятный неконтролируемый алгоритм, способный очень быстро выявлять выбросы или аномалии в наборе данных. Я должен сказать, что понимание этого инструмента является обязательным для любого начинающего специалиста по данным. В этой статье я кратко расскажу о теориях алгоритма, а также о его реализации.

Его реализация на Python от Scitkit Learn набирает популярность благодаря своим возможностям и простоте использования. Но прежде чем мы перейдем непосредственно к реализации, нам всегда лучше изучить варианты ее использования и лежащую в ее основе теорию. Тем не менее, не стесняйтесь сразу переходить к части реализации!

Некоторые теории

Во-первых, что такое аномалия?

Аномалию (выброс) можно описать как точку данных в наборе данных, которая значительно отличается от других данных или наблюдений. Это может произойти по нескольким причинам:

• Выбросы могут указывать на плохие данные, которые неверны, или эксперимент мог быть проведен неправильно.

• Выброс может быть вызван случайным изменением или может указывать на что-то интересное с научной точки зрения.

Это довольно упрощенная версия аномалии. Тем не менее, оба события — это то, что ученые данных хотели бы понять и углубиться в них.

Почему обнаружение аномалий?

Причина, по которой мы хотели бы углубиться в аномалии, заключается в том, что эти точки данных либо запутают вас, либо позволят вам определить что-то значимое.

В случае простой линейной регрессии плохой выброс может увеличить дисперсию в нашей модели и еще больше снизить способность нашей модели улавливать данные. Выбросы приводят к тому, что модели регрессии (особенно линейные) изучают искаженное понимание в сторону выброса.

Обзор изолированного леса

Традиционно другие методы пытались создать профиль нормальных данных, а затем определить, какие точки данных не соответствуют профилю как аномалии.

Отличительной чертой Isolation Forest является то, что он может напрямую обнаруживать аномалии, используя изоляцию (насколько далеко точка данных находится от остальных данных). Это означает, что алгоритм может работать с линейной временной сложностью, как и другие модели, связанные с расстоянием, такие как K-ближайшие соседи.

Алгоритм работает, опираясь на наиболее очевидные атрибуты выброса:

• Будет только несколько отклонений

• Их выбросы будут другими

Isolation Forest делает это, вводя (ансамбль) бинарных деревьев, которые рекурсивно генерируют разделы путем случайного выбора функции, а затем случайным выбором значения разделения для функции. Процесс разделения будет продолжаться до тех пор, пока он не отделит все точки данных от остальных выборок.

Поскольку из экземпляра для каждого дерева выбирается только одна функция, мы можем сказать, что максимальная глубина дерева решений на самом деле равна единице. Фактически, базовая оценка Изолирующего леса на самом деле является чрезвычайно случайным деревом решений (ExtraTrees) для различных подмножеств данных.

Пример одиночного дерева в изолированном лесу можно увидеть ниже.

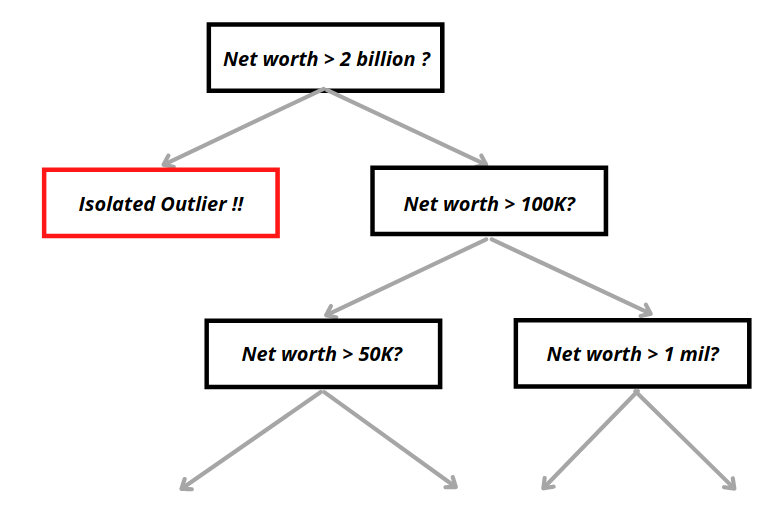
Учитывая атрибуты выброса, упомянутые выше, мы можем заметить, что выбросу потребуется в среднем меньше разделов для их изоляции по сравнению с обычными выборками. Затем каждая точка данных получит оценку, основанную на том, насколько легко они изолируются после X раундов. Точки данных с аномальными оценками будут помечены как аномальные.

На изображении ниже из IEEE показано разделение выбросов с двумерной точки зрения.

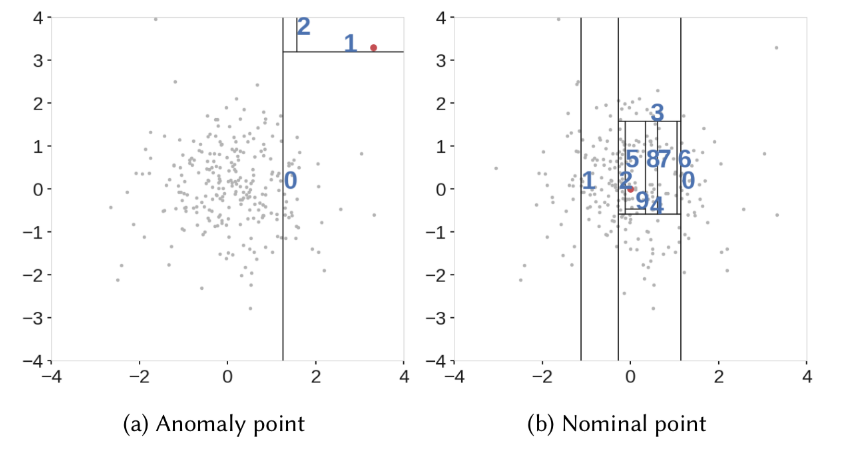
Источник: [IEEE] (https://ieeexplore.ieee.org/abstract/document/8888179).

Говоря более формально, мы рекурсивно разделяем каждый экземпляр данных, случайным образом выбирая атрибут q и значение разделения p (в пределах минимального и максимального значения атрибута q), пока все они не будут полностью изолированы. Затем изолированный лес предоставит ранжирование, отражающее степень аномалии каждого экземпляра данных в соответствии с длиной их пути.

Рейтинг или баллы называются баллами аномалий, которые рассчитываются следующим образом:

• H(x): количество шагов до полной изоляции экземпляра данных x.

• E[H(x)] : среднее значение H(x) из набора изолированных деревьев.

Метрики имеют смысл, но одна проблема заключается в том, что максимально возможные шаги iTree растут в порядке n, в то время как средние шаги растут только в порядке log n. Это приведет к проблемам, когда шаги нельзя сравнивать напрямую. Следовательно, необходимо ввести нормировочную константу, изменяющуюся на n.

c(n), константа нормализации со следующей формулой, представленной в исходной статье:

где H(i) — номер гармоники, который можно оценить как ln(i) + 0,5772156649 (постоянная Эйлера).

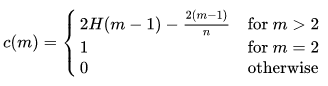
Полное уравнение оценки аномалии, представленное в [исходной статье] (https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf?q=isolation-forest):

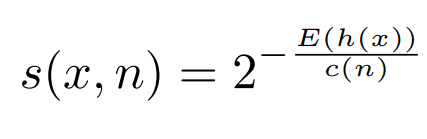
Следовательно, если мы пропустим весь набор данных через изолированный лес, мы сможем получить его показатель аномалии. Используя показатель аномалии s, мы можем сделать вывод, существуют ли аномалии всякий раз, когда есть экземпляры с показателем аномалии, очень близким к единице. Любая оценка ниже 0,5 будет считаться нормальным экземпляром.

:::Информация

В реализации sklearn оценки аномалий противоположны оценке аномалий, определенной в исходной статье. Далее они вычитаются с константой 0,5. Это делается для того, чтобы легко идентифицировать аномалии (отрицательные баллы идентифицируются с аномалиями).

[Подробнее] (https://github.com/scikit-learn/scikit-learn/blob/37ac6788c9504ee409b75e5e24ff7d86c90c2ffb/sklearn/ensemble/_iforest.py#L345)

Реализация изолированного леса

Закончили со всеми теориями? Давайте определим некоторые выбросы.

Во-первых, мы быстро импортируем некоторые полезные модули, которые будем использовать позже. Мы генерируем набор данных со случайными точками данных, используя функцию make_blobs().

```питон

импортировать numpy как np

импортировать панд как pd

импортировать matplotlib.pyplot как plt

из sklearn.datasets импортировать make_blobs

данные, _ = make_blobs (n_samples = 500, center = 1, cluster_std = 2, center_box = (0, 0))

plt.scatter (данные [:, 0], данные [:, 1])

plt.show()

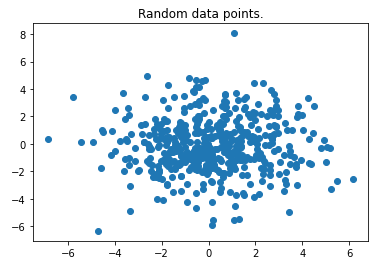
Мы можем легко увидеть некоторые выбросы, так как это только вариант использования 2-D. Это хороший выбор, чтобы доказать, что алгоритм работает. Обратите внимание, что алгоритм можно без проблем использовать для набора данных с несколькими функциями.

Мы инициализируем объект изолированного леса, вызывая IsolationForest().

Используемые здесь гиперпараметры в основном установлены по умолчанию и рекомендованы в оригинальной статье.

Мы обнаружили, что длины путей обычно сходятся задолго до t = 100. Эмпирически мы обнаружили, что установка выборки подмножества на 256 обычно обеспечивает достаточно деталей для обнаружения аномалий в широком диапазоне данных.

— Fei Tony Liu, Kai Ming Ting

• Здесь N_estimators обозначает количество деревьев, а максимальная выборка здесь обозначает выборку подмножества, используемую в каждом раунде.

• Max_samples = 'auto' устанавливает размер подмножества как минимум (256, num_samples).

• Параметр загрязнения здесь означает долю выбросов в наборе данных. По умолчанию пороговое значение оценки аномалии будет таким же, как и в оригинальной статье. Однако мы можем вручную исправить долю выбросов в данных, если у нас есть какие-либо предварительные знания. Мы установили его на 0,03 здесь для демонстрационных целей.

Затем мы подгоняем и прогнозируем весь набор данных. Он возвращает массив, состоящий из [-1 или 1], где -1 означает аномалию, а 1 — нормальный экземпляр.

```питон

iforest = IsolationForest (n_estimators = 100, загрязнение = 0,03, max_samples = 'auto)

прогноз = iforest.fit_predict (данные)

печать (прогноз [: 20])

print("Количество обнаруженных выбросов: {}".format(prediction[prediction < 0].sum()))

print("Количество обнаруженных нормальных выборок: {}".format(prediction[prediction > 0].sum()))

Затем мы нанесем на график выбросы, обнаруженные Isolation Forest.

```питон

normal_data = данные [np.where (прогноз > 0)]

выбросы = данные [np.where (прогноз <0)]

plt.scatter(normal_data[:, 0], normal_data[:, 1])

plt.scatter (выбросы [:, 0], выбросы [:, 1])

plt.title("Случайные точки данных с выявленными выбросами.")

plt.show()

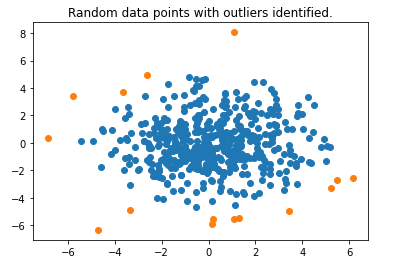
Мы видим, что он работает довольно хорошо и идентифицирует точки данных по краям.

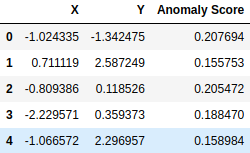
Для вычисления оценки аномалии каждой точки данных может быть вызвана функция решения_функции(). Таким образом, мы можем понять, какие точки данных более ненормальны.

```питон

оценка = функция iforest.decision_function (данные)

data_scores = pd.DataFrame (список (zip (данные [:, 0], данные [:, 1], оценка)), \

столбцы = ['X','Y','Оценка аномалии'])

дисплей (data_scores.head())

Мы выбираем 5 лучших аномалий, используя оценки аномалий, а затем снова наносим их на график.

```питон

top_5_outliers = data_scores.sort_values(by = ['Оценка аномалии']).head()

plt.scatter (данные [:, 0], данные [:, 1])

plt.scatter(top_5_outliers['X'], top_5_outliers['Y'])

plt.title("Случайные точки данных только с 5 идентифицированными выбросами.")

plt.show()

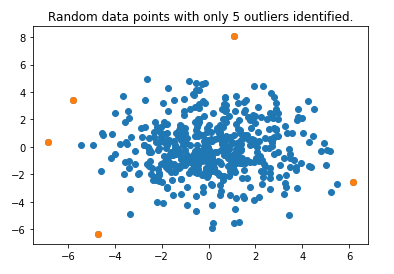
Забрать

Изолирующий лес — это принципиально другая модель обнаружения выбросов, которая может изолировать аномалии с большой скоростью. Он имеет линейную временную сложность, что делает его одним из лучших для работы с большими объемами данных.

Он основан на концепции, согласно которой, поскольку аномалий «несколько и они разные», их легче изолировать по сравнению с нормальными точками. Его реализацию на Python можно найти по адресу sklearn.ensemble.IsolationForest.

Спасибо, что нашли время в своем плотном графике, чтобы посидеть со мной и насладиться этим прекрасным алгоритмом.

Ссылка

[Изолирующий лес] (https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf?q=isolation-forest) Фей Тони Лю, Кай Мин Тинг Гиппсленд Школа информационных технологий Университета Монаша , Виктория, Австралия.

Также опубликовано [здесь] (https://medium.com/@limyenwee_19946/unsupervised-outlier-detection-with-isolation-forest-eab398c593b2).