Поддающиеся проверке вычисления, сохраняющие конфиденциальность: Поддающиеся проверке вычисления, сохраняющие конфиденциальность.
10 января 2024 г.:::информация Этот документ доступен на arxiv по лицензии CC 4.0.
Авторы:
(1) Тарик Бонтекое, Гронингенский университет;
(2) Димка Карастоянова, Гронингенский университет;
(3) Фатих Туркмен, Гронингенский университет.
:::
Таблица ссылок
Доказательства с нулевым разглашением и проверяемые вычисления
Вычисления, обеспечивающие конфиденциальность
Требования: точка зрения приложения
Проверяемые вычисления с сохранением конфиденциальности
Открытые проблемы и будущие направления
6. Поддающиеся проверке вычисления с сохранением конфиденциальности
Все больше статей обсуждает сочетание ПЭТ с проверяемыми вычислениями в условиях, где должны быть гарантированы как конфиденциальность, так и корректность. В этом разделе мы собираем, классифицируем и сравниваем существующие работы, которые добавляют (публичную) проверяемость к (децентрализованным) вычислениям, сохраняющим конфиденциальность. Кроме того, мы отвечаем на следующий вопрос RQ3: Насколько существующие решения соответствуют требованиям/свойствам раздела 5?
6.1. Методология
Чтобы получить полный список текущих работ, мы сначала определили небольшой набор недавних соответствующих статей о (публично) проверяемых/проверяемых вычислениях, сохраняющих конфиденциальность. В частности, мы определили по крайней мере одну совсем недавнюю «исходную» статью о различных базовых (сохраняющих конфиденциальность) вычислительных методах, запросив базы данных Google Scholar и Scopus. Самый последний на момент написания поддающийся проверке документ MPC [72] был найден по запросу: (публичная проверяемость ИЛИ публичный аудит) AND (MPC OR SMPC OR многостороннее вычисление OR безопасное многостороннее вычисление). Две актуальные, недавние поддающиеся проверке статьи HE [73], [74] были найдены с использованием: (проверяемый ИЛИ общедоступная проверяемость ИЛИ общедоступная проверяемость) И (гомоморфное шифрование ИЛИ полностью гомоморфное шифрование). Окончательный исходный документ [54] о вычислениях, сохраняющих конфиденциальность на основе DLT, заранее был известен как недавний и актуальный, поэтому конкретный запрос не использовался.
В дальнейшем мы проверили все статьи в списке литературы этих «начальных» статей второй степени. Помимо этого, были также проверены все статьи, в которых ссылались на наши «начальные» статьи. Отфильтровав статьи по их релевантности на основе названия, аннотации и быстрого сканирования, мы нашли 32 релевантные работы, представляющие новое или улучшенное решение для проверяемых вычислений, сохраняющих конфиденциальность.
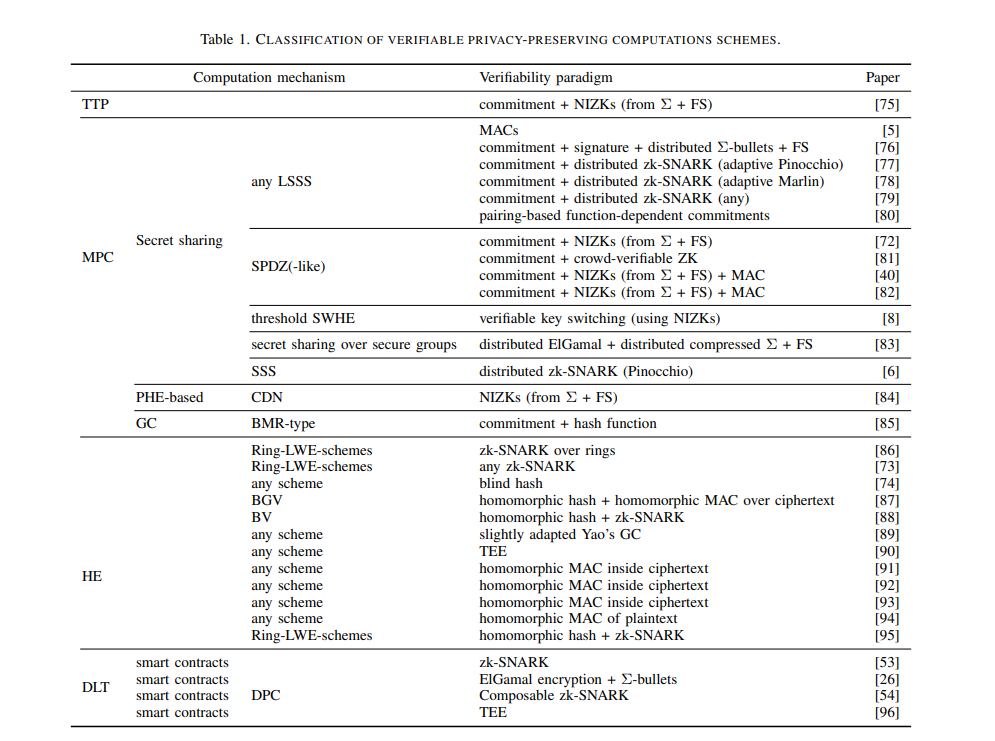
6.2. Классификация
В Таблице 1 представлен обзор всех документов и конструкций, используемых для сочетания конфиденциальности и проверяемости, классифицированных в соответствии с использованным базовым вычислительным механизмом. В тексте ниже мы более подробно обсуждаем решения для каждого используемого механизма проверки: ZKP, MAC, TEE и другие подходы.
Доказательства с нулевым разглашением. ZKP используются в подходах MPC, HE и DLT. Большинство решений на основе MPC полагаются на ту или иную форму LSSS, например, схемы совместного использования секрета Шамира (SSS) [31] или схемы SPDZ(-like) [32]. Подходы с использованием PHE (например, CDN [97]) или GC наблюдались реже.
МПЦ. В большинстве поддающихся проверке решений MPC используются обязательства по секретности долей входных/выходных значений и промежуточные вычисления в сочетании с NIZK для гарантии правильности. Мы различаем три типа НИЗК, которые используются с разными свойствами. В первой серии работ [40], [72], [82], [84] используются Σ-протоколы и эвристика FS для получения НИЗК из стандартных предположений. Два протокола типа SPDZ ([40], [82]) дополнительно полагаются на MAC-адреса, аналогичные тем, которые использовались в исходном протоколе SPDZ. Недостатком Σ-протоколов является большой размер доказательства и значительные усилия, необходимые со стороны верификатора для более крупных вычислений. Следовательно, в недавних работах [76], [83] часто применяется более эффективная теория сжатого Σ-протокола [27] или Σ-пули [26], которая обеспечивает аналогичные гарантии безопасности.
В других работах [6], [77], [78], [79] в качестве еще более эффективного подхода используются распределенные, часто адаптивные zk-SNARK для обеспечения корректности. [81] представляет решение на основе MPC, основанное на проверяемых толпой ZKP. Это означает, что проверяющий пытается убедить группу проверяющих («толпу»), где каждый проверяющий обеспечивает лишь ограниченную степень случайности, поэтому требуется в основном честная толпа.
ОН. Лишь в последние годы появились первые решения с использованием ЗКП для создания проверяемых ВО. В [88] представлен первый zk-СНАРК, подходящий для схемы BV [98]. Однако для схемы FHE требуются определенные параметры настройки, соответствующие групповым порядкам zk-SNARK, что приводит к снижению эффективности операций FHE.
[95] усовершенствовали эту работу, не ограничивая пространство параметров HE. Однако оба решения ограничены «более простыми» схемами FHE, т. е. без сложных операций обслуживания зашифрованного текста, поскольку они не поддерживаются используемой схемой гомоморфного хеширования. [86] предлагает метод, который не полагается на гомоморфные хеши, а скорее использует Rinocchio: zk-SNARK, который эффективно работает с кольцами.
[73, разд. 5.1] сравнивает Rinocchio с тремя популярными эффективными ZKP и показывает уменьшение времени проверки в ~1,5–25000 раз. Открытым вопросом для Риноккио является то, как выполнять операции по обслуживанию зашифрованного текста. Обычно это требует операций, не поддерживаемых кольцами, или переключения между разными кольцами, что не поддерживается Rinocchio.
ДЛТ. Некоторые схемы не полагаются на конкретный PET для вычислений, сохраняющих конфиденциальность. Вместо этого они объединяют DLT с ZKP для достижения аналогичного результата. Особенно это касается использования zk-SNARK из-за их небольшого, часто постоянного, контрольного размера и эффективной проверки. Хотя большинство приложений ориентированы исключительно на финансовые транзакции, например Zerocash [7], мы также выделяем работы, ориентированные на смарт-контракты. [26] предлагает Σ-пули для создания платежной системы, сохраняющей конфиденциальность, на платформах смарт-контрактов. Однако предоставляемая функциональность не распространяется напрямую на вычисления, связанные с неплатежами. [53] предлагает структуру Hawk для проверки общих функций смарт-контрактов при сохранении конфиденциальности ввода и вывода с использованием zk-SNARK. DPC, предложенный в [54], можно рассматривать как развитие Hawk, который также обеспечивает конфиденциальность функций с использованием компонуемых zk-SNARK. Отметим, что все эти работы проверяют только локальные вычисления, выполненные одной стороной. Однако благодаря публикации результатов и доказательств в блокчейне вся система может использоваться для проверяемых, сохраняющих конфиденциальность вычислений с участием нескольких сторон.
MAC. Коды аутентификации сообщений преимущественно используются в подходах HE, но также встречаются и для MPC.
МПЦ. Хотя MAC часто используются для достижения активной безопасности в MPC, например, SPDZ [32], неясно, как добиться публичной проверяемости, поскольку для проверки часто приходится полагаться на секретный ключ. [5] использует MAC для разработки схемы, в которой n клиентов передают проверяемые вычисления на аутсорсинг m работникам. Однако только клиенты могут проверить вычисления, и хотя бы один работник должен действовать честно, чтобы гарантировать правильность и конфиденциальность данных.
ОН. Мы видим три различных подхода к объединению шифртекстов HE и MAC, согласуясь с [73]: (1) Encryptthen-MAC; (2) Шифрование и MAC; (3) MAC-затем шифровать.
Подход Encrypt-then-MAC используется в [87]. Авторы предлагают сначала гомоморфно хешировать зашифрованные тексты BGV [99], а затем добавлять гомоморфный MAC, вычисленный на основе этого хэша. Однако представленное решение довольно ограничено и поддерживает только квадратичные схемы. Из-за отсутствия других работ, использующих этот подход, неясно, можно ли его обобщить на общие арифметические схемы.
Подходы с шифрованием и MAC имеют MAC и зашифрованный текст, которые независимы друг от друга, оба вычисляются непосредственно из открытого текста. Таким образом, MAC должен одновременно скрывать и поддерживать операции с зашифрованным текстом, необходимые для схемы FHE. [94] представляет гомоморфный MAC, сохраняющий конфиденциальность, который поддерживает операции умножения и сложения. Этот примитив впоследствии используется для создания эффективной конструкции шифрования и MAC для HE. Однако неясно, как MAC поддерживает другие типы операций, необходимые для большинства схем FHE.
Мы обнаружили, что наиболее распространенным подходом из трех является MAC-then-Encrypt, где MAC вычисляется из открытого текста и объединяется с открытым текстом перед шифрованием. [91] является первым, кто представил полностью гомоморфную схему MAC, которую можно использовать для проверки вычислений HE над логическими схемами. Хотя MAC в этой схеме кратки, использование этого подхода для проверки вычислений HE не более эффективно, чем выполнение самих вычислений. Усовершенствование этой схемы с более эффективной проверкой вычислений HE на арифметических схемах предложено в [92]. Однако этот подход ограничен арифметическими схемами ограниченной глубины. [93], более поздняя работа, использующая тот же подход, не имеет ни одного из этих ограничений и, таким образом, может использоваться для проверки оценок HE любой арифметической схемы.
Ни одна из вышеперечисленных схем не подлежит публичной проверке, поскольку для проверки MAC требуется доступ к полному секретному ключу.
Доверенная среда выполнения. TEE — это собирательное название (в основном) аппаратных решений, которые защищают конфиденциальность данных, одновременно позволяя использовать эти данные в вычислениях. Для TEE требуется специальное оборудование, например Intel SGX или AMD SEV, которое выполняет вычисления на основе зашифрованных данных, расшифровывая их только внутри защищенной части ЦП. Некоторые TEE также предоставляют механизмы аттестации для проверки кода, работающего внутри.
[96] предлагает Ekiden, блокчейн-решение, в котором смарт-контракты с личными данными выполняются вне цепочки. Специализированные вычислительные узлы с TEE выполняют смарт-контракт и публикуют удаленную аттестацию для правильного выполнения. Узлы консенсуса, в свою очередь, должны иметь возможность проверять эти аттестации для обновления результатов смарт-контракта в сети.
[90] представляет конструкцию FHE в TEE, в которой также используется аттестация TEE. Клиенты могут отправлять свои зашифрованные данные в TEE в облаке, и им нужно только подтвердить, что он выполняет именно правильные вычисления. TEE, естественно, поддерживают больше вычислений, чем другие подходы, однако поддерживаемые операции более ограничены и значительно медленнее, чем когда они выполнялись обычными процессорами. Оптимизация вычислений FHE для TEE может привести к заметному повышению производительности [73].
Для обоих подходов неясно, как добиться публичной проверки, т. е. как аттестация может (эффективно) выполняться внешними сторонами. Более того, хотя TEE зачастую относительно эффективны по сравнению с другими методами, они требуют доверия к используемому специализированному оборудованию.
Другое. Некоторые работы не подошли ни к одной из вышеперечисленных категорий. Тем не менее, эти подходы заслуживают упоминания.
[75] передает все вычисления доверенной третьей стороне (TTP). Этот TTP создает доказательства NIZK, чтобы гарантировать правильность, и ему доверяют сохранять конфиденциальность ввода. Это решение относительно эффективно, однако во многих реальных случаях требовать TTP нереально.
[80] представляет создание экземпляров функционально-зависимых обязательств на основе пар, что приводит к эффективной проверке правильности. Однако предложенная конструкция поддерживает только линейные функции, и неясно, можно ли ее распространить на нелинейные функции.
[85] представляет эффективный, постоянный раунд, публично проверяемый протокол MPC, который использует только криптографические примитивы в «черном ящике». Их решение основано на искаженной схеме типа BMR [37] и требует доступа к «черному ящику» к статистически безопасной схеме OT и устойчивой хеш-функции с циклической 2-корреляцией. Примечательно, что правильность и публичная проверка справедливы только при наличии хотя бы одной честной стороны.
[8] строит протокол MPC, используя схему SWHE, поддерживающую одно умножение. Поддающееся проверке переключение ключей с использованием NIZK принято для поддержки вычислений с произвольным количеством умножений.
[74] представляет подход к проверяемому FHE, который называется «слепым хешированием», при котором хэш открытого текста добавляется к открытому тексту перед шифрованием, т. е. это очень похоже на MAC-then-Encrypt. Хэш впоследствии проверяется путем вычисления хеша расшифрованного результата и обеспечения его соответствия хешу, включенному в зашифрованный текст. Мы отмечаем, что в этой предварительной публикации отсутствуют доказательства безопасности или обоснования, и в ней объясняется только то, как выполнить одно матричное умножение. Неясно, как этот подход распространяется на другие операции, например, необходимые для обслуживания зашифрованного текста и более сложных схем.
Наконец, [89] предлагает использовать GC Яо [35] для однократных проверяемых вычислений между клиентом и сервером. Впоследствии они предлагают добавить FHE сверху, чтобы превратить этот одноразовый подход в многоразовый, позволяющий многократно выполнять одну и ту же функцию на разных входных данных. Следует отметить, что для другого вычисления требуется новая настройка, а вычисление этой настройки довольно неэффективно.
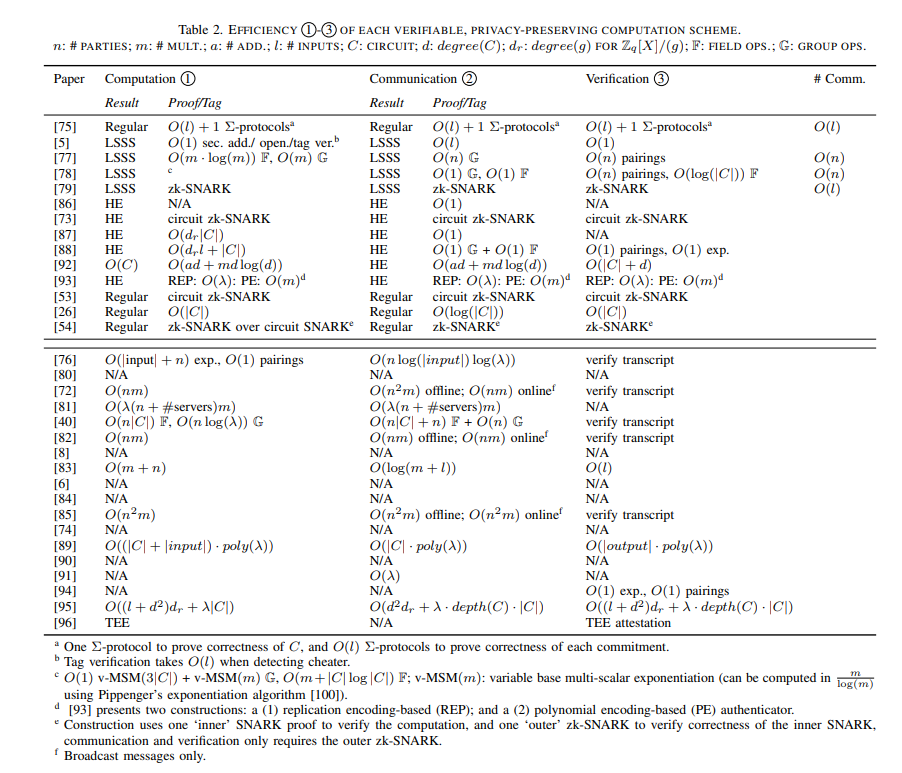
6.3. Эффективность 1–3
Обзор асимптотических сложностей каждой схемы представлен в таблице 2. В случае, если авторы не упомянули сложность своего решения в статье, и мы не смогли найти ее в связанных работах, мы пометили ее как 'N /А'.
В частности, мы описываем сложность вычислений (1) и связи (2) проверяемых вычислений. По возможности мы разделяем затраты между затратами на создание результата функции и затратами на создание доказательства или тега, необходимого для проверки. Если в решении используется общий строительный блок, вместо указания точной используемой схемы мы описываем тип используемого строительного блока, например, LSSS, HE или zk-SNARK. Поскольку проверка (3) выполняется отдельно от вычислений в случае публичной проверяемости, мы перечисляем ее сложность в отдельном столбце.
Наконец, мы перечисляем асимптотическое количество обязательств, используемых каждым решением, если они используются и если их сложность еще не включена в другие столбцы. Обязательства приводят к дополнительным затратам на вычисления и связь, в зависимости от конкретной используемой схемы обязательств.
Короче говоря, мы наблюдаем, что подходы MPC имеют более высокую коммуникацию и более низкую стоимость вычислений, чем подходы, основанные на HE. Более того, мы видим, что подходы на основе MAC и zk-SNARK имеют эффективную проверку, особенно по сравнению с другими подходами. MAC часто требуют большего объема связи, чем zk-SNARK, но они более эффективны в вычислительном отношении.
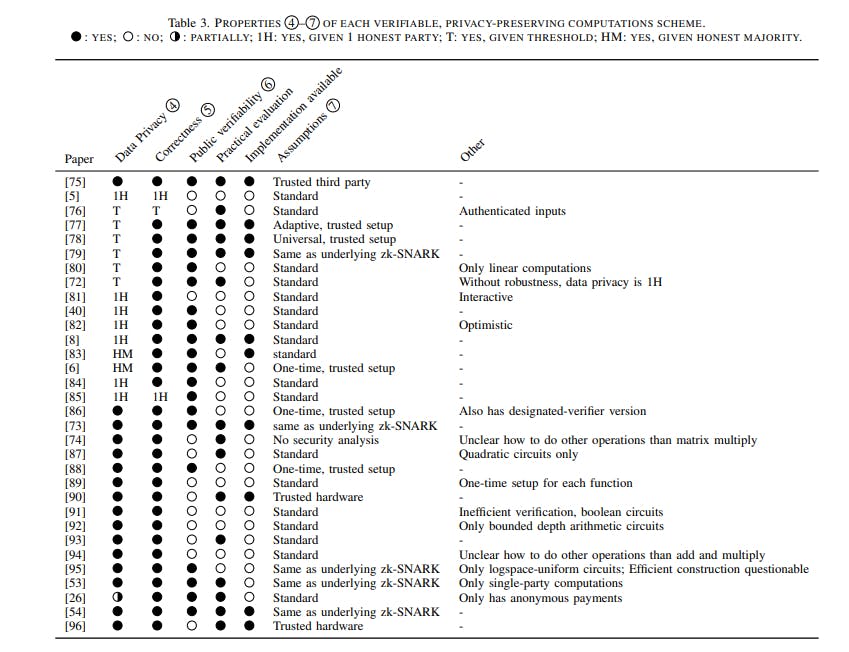
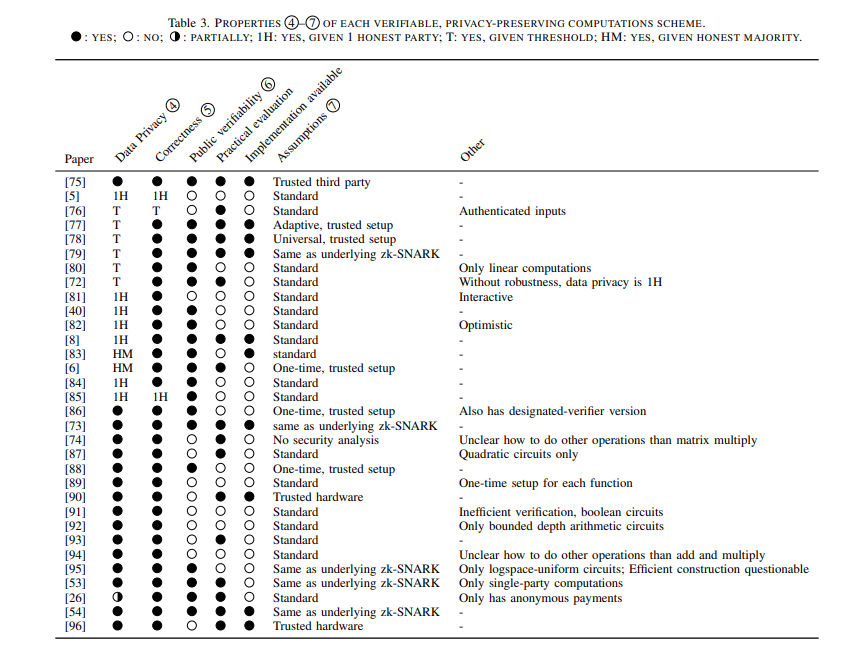
6.4. Свойства 4 – 8
На основе обсуждения в разделе 5 мы отметили несколько важных аспектов, которые определяют пригодность схемы для нескольких областей. В Таблице 3 представлен обзор соответствующих аспектов безопасности и удобства использования. Рядом с этим мы указываем, оценивалось ли в исходной работе их решение в практическом сценарии, и предоставляют ли они общедоступную реализацию. Ниже мы сравниваем различные подходы к решению, обсуждая наиболее яркие наблюдения и проблемы для будущей работы.
Конфиденциальность данных 4. Существует заметная разница между решениями на основе MPC и HE в отношении допущений, для которых они обеспечивают конфиденциальность данных. Во многом это связано с тем, что MPC распределяет данные между несколькими сторонами, тогда как решения на базе HE обычно отправляют все свои данные на центральный вычислительный сервер.
В решениях на базе MPC конфиденциальность зависит от используемой схемы. Хотя некоторые схемы гарантируют конфиденциальность, когда честна только одна из сторон, другие требуют честного большинства.
Для HE гарантируется конфиденциальность данных каждого зашифрованного текста, и только стороны, владеющие секретным ключом, могут просматривать частные данные. Однако во многих случаях использования распределенных данных или децентрализованных вычислений входные данные должны быть зашифрованы с помощью общего секретного ключа. В этом случае справедливы те же наблюдения, что и для решений на основе MPC.
Правильность и общедоступность 5 & 6 . Хотя почти все схемы обеспечивают безусловную правильность, этого нельзя сказать о публичной проверке. Большинство решений HE не обеспечивают публичной проверки, в отличие от решений на основе MPC. Причина этого, скорее всего, связана с тем, что большинство решений HE полагаются на MAC.

Кроме того, сочетание схем ZKP и HE в настоящее время слишком неэффективно и ограничено.

Предположения о безопасности 7 & 8. Мы определяем три основные группы предположений безопасности. Первая группа полагается на TEE как для конфиденциальности, так и для корректности. Хотя эти схемы не требуют каких-либо нестандартных криптографических предположений и к тому же очень эффективны, они требуют доступа к очень специфическому оборудованию и доверия к нему. Из-за недавних атак на аппаратное обеспечение ЦП, например Spectre и Meltdown, стороны могут не захотеть использовать это.
Вторая группа использует zk-SNARK для обеспечения публичной проверки. Эти схемы, как известно, очень эффективны, но в свою очередь должны полагаться на нестандартные криптографические предположения, такие как предположения типа знания экспоненты. Более того, многие из этих схем полагаются на надежную настройку для обеспечения безопасности, что во многих случаях может быть нежелательным.
Последняя группа состоит из конструкций, опирающихся преимущественно на Σ-протоколы и MAC. Такие конструкции часто менее эффективны, но они компенсируют это, полагаясь только на стандартные криптографические предположения, не требуя специального оборудования.

Что касается постквантовой безопасности ( 8 ), мы отмечаем, что большинство схем HE сами по себе являются постквантовыми безопасными, и поэтому многие из обсуждавшихся выше конструкций на основе MAC, вероятно, получают это свойство, даже если это напрямую не обсуждается. . Однако большинство конструкций на основе MPC не являются постквантовыми. Только [72] использует в основном постквантовые безопасные примитивы. Несмотря на то, что он не является полностью постквантовым, с некоторыми небольшими изменениями он, скорее всего, будет.

Оригинал

