Коэффициент инфляции дисперсии — подходящая статистическая метрика для распознавания мультиколлинеарности

3 февраля 2023 г.

Введение

Благодаря достижениям в области машинного и глубокого обучения у нас есть целый арсенал алгоритмов, способных справиться с любой проблемой, которую мы перед ними ставим. Но у большинства этих изощренных и сложных алгоритмов есть проблема; они должны быть проще для понимания.

Ничто не сравнится с простотой и интерпретируемостью линейной регрессии, когда речь идет о интерпретируемости моделей машинного обучения. Однако могут возникнуть некоторые проблемы с интерпретируемостью линейной регрессии, особенно если предположения о мультиколлинеарности линейной регрессии нарушаются.

В этой статье мы рассмотрим концепцию мультиколлинеарности, ее обнаружение и анализ. обработка с помощью жизненно важной статистической метрики — «Коэффициент инфляции дисперсии».

Концепция мультиколлинеарности n

Фактор увеличения дисперсии – это статистический показатель, используемый для обнаружения мультиколлинеарности в моделях прогнозирования с учителем.

Прежде всего, давайте разберемся с концепцией мультиколлинеарности, прежде чем погрузиться в интуицию VIF. Учтите, что нам нужно построить регрессионную модель для прогнозирования зарплаты человека. В нашем наборе данных есть следующие независимые переменные:

1. Возраст
2. Многолетний опыт
3. Задание
4. Пол
5. Город
6. Индекс стоимости жизни в месте проживания

Наши данные выглядят так-

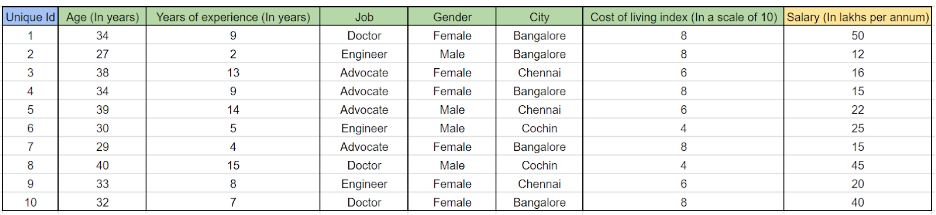
Итак, это традиционная задача множественной линейной регрессии, и любая множественная линейная регрессия может быть представлена ​​с помощью математической формулы-

<цитата>

Y = m1x1 + m2x2 + m3x3+.....+mnxn + c

Где,

• Y – целевая переменная.
• x1, x2, x3…xn — независимые переменные
• m1, m2, m3, mn — все наклоны x1, x2, x3 и xn соответственно.
• c — это точка пересечения

В соответствии с нашим вариантом использования мы определяем нашу проблему как-

<цитата>

Зарплата = (0,5 * Возраст) + (0,6 * Годы опыта) + (0,1 * Работа) + (0,2 * Пол) + (0,6 * Город) + 0,7 (индекс стоимости жизни)

(Просто примите некоторые случайные значения для коэффициентов или наклонов, чтобы понять концепцию простым способом).

Приведенная выше формула по сути означает, что-

1. Всякий раз, когда возраст увеличивается на одну единицу, зарплата увеличивается на 0,5 единицы, при этом все остальные переменные остаются неизменными.
2. Всякий раз, когда индекс стоимости жизни увеличивается на одну единицу, зарплата увеличивается на 0,7 единицы, при этом все остальные переменные остаются неизменными.

Теперь мы можем логически подумать о нескольких вещах в соответствии с реальным сценарием:

1. Кажется, что все вышеупомянутые независимые переменные имеют некоторую связь с целевой переменной (зарплатой).
2. Однако мы знаем, что между возрастом и стажем существует прямолинейная зависимость. Предполагая, что человек начинает работать в возрасте около 25 лет, его/ее трудовой стаж будет увеличиваться на один год всякий раз, когда его/ее возраст увеличивается на один год.

Основная цель любой регрессионной модели — узнать о дисперсии в наборе данных. Таким образом, нахождение того, как каждая из независимых переменных влияет на целевую переменную (путем определения правильного значения коэффициента), и прогнозирование цели для невидимых точек данных. Всякий раз, когда мы используем конкретную независимую переменную, она должна быть способна предоставить модели некоторую информацию о целевой переменной, которую другие переменные не могут зафиксировать. Если 2 переменные объясняют одну и ту же дисперсию (влияя на целевую переменную примерно уникальным образом), то нет смысла сохранять обе независимые переменные, поскольку это будет дополнительным бременем для модели, которая может увеличить временную и пространственную сложность без каких-либо последствий. использование.

Например,

Считайте, что у вас есть 4 друга: Джон, Джеймс, Джозеф и Джек. Все пошли смотреть фильм. К сожалению, вы не смогли купить билеты. Итак, ваши друзья сказали, что будут смотреть фильм и объяснять сюжет сцена за сценой. Продолжительность фильма 3 часа.

Предположим, что-

1. Джон рассказал историю первых 60 минут.
2. Джеймс объяснил историю с 61-й по 120-ю минуту.
3. Джозеф объяснил историю со 121-й по 180-ю минуту.

Теперь очередь Джека. Он не знает, что остальные трое уже рассказали все части истории. Он снова объяснил вам историю со 121-й по 180-ю минуту.

Итак, вы дважды слышали историю последних 60 минут. Либо Джозефа, либо Джека было достаточно, чтобы объяснить последние 60 минут. Поскольку они оба объяснили одно и то же, они не могут предоставить вам никакой дополнительной информации. Технически вы слушали историю 240 минут, хотя всю информацию можно охватить за 180 минут. Время и силы, потраченные Джеком, пропали даром, и вы тоже потеряли время, услышав ненужную информацию.

Значит, Джек и Джозеф мультиколлинеарны!!!

Мультиколлинеарность относится к ситуации, в которой более двух независимых переменных в модели множественной регрессии тесно связаны линейно.

У вас возникнут очевидные сомнения в том, в чем проблема, если две переменные сильно коллинеарны.

Мы обсудили коэффициенты в формуле множественной линейной регрессии

Согласно нашей постановке задачи, это -

Зарплата = (0,5 * возраст) + (0,6 * многолетний опыт) + (0,1 * работа) + (0,2 * пол) + (0,6 * город) + 0,7 (индекс стоимости жизни)

Здесь мы знаем, что возраст и многолетний опыт тесно связаны.

• Если мы удалим одну из этих коллинеарных переменных из модели, мы увидим, что модель адаптируется к новому набору коэффициентов для всех независимых переменных.
• Иногда наличие приблизительной коллинеарности может не привести к резкому снижению прогностической способности модели, но, безусловно, увеличит временную и пространственную сложность модели.
• Однако, если несколько переменных полностью коррелированы, это может привести к краху модели, что приведет к снижению производительности.
• Чтобы сохранить предположения линейных моделей, мы никогда не должны рисковать, включая несколько коллинеарных переменных. Линейная модель всегда предполагает, что все переменные-предикторы совершенно независимы, т. е. конкретная переменная-предиктор не может быть объяснена путем установления некоторых отношений между некоторыми другими переменными-предикторами в данных. В таком сценарии все коэффициенты будут очень эффективными, что приведет к обобщенной гиперплоскости, которая может поддерживать согласованность прогноза в любом невидимом наборе точек данных n

Основная интуиция, стоящая за VIF

n Следующий вопрос -

<цитата>

Как определить, присутствует ли в наборе данных мультиколлинеарность?

Ответ: «ВИФ».

Теперь давайте разберемся с интуицией, лежащей в основе VIF.

Ранее мы обсуждали, что конкретная предикторная переменная не может быть объяснена путем установления некоторых отношений между некоторыми другими предикторными переменными в данных.

Прежде чем перейти к примеру, давайте разберемся со значением R в квадрате.

Квадрат R, также известный как Коэффициент детерминации, является одним из наиболее широко используемых показателей оценки для моделей линейной регрессии. R в квадрате считается показателем качества подгонки, который большую часть времени находится в диапазоне от 0 до 1. Чем выше значение R в квадрате, тем выше согласованность и прогностическая способность модели.

VIF представлен математической формулой-

<цитата>

VIF – 1/(1-R в квадрате).

Чтобы определить мультиколлинеарность, нам нужно получить VIF всех переменных-предикторов, присутствующих в наборе данных.

Допустим, если нам нужно рассчитать VIF для возраста, мы должны рассматривать «Возраст» как целевую переменную, а все остальные переменные-предикторы как независимые переменные и должны разработать модель множественной линейной регрессии.

Например,

Чтобы найти VIF возраста,

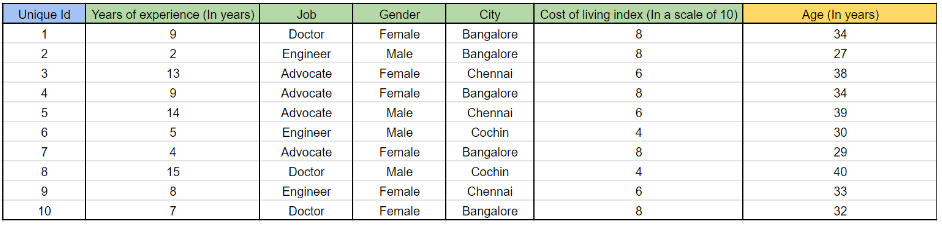Давайте построим такую ​​модель-

Возраст = (0,6 * годы опыта) + (0,1 * работа) + (0,2 * пол) + (0,6 * город) + 0,7 (индекс стоимости жизни)

Для этой модели мы получим значение R в квадрате.

n Предположим, что полученное нами значение R в квадрате равно 0,85

Сейчас

VIF = 1 /(1-0,85)

ВИФ = 1/0,15

ВИФ = 6,67

Здесь следует отметить одну вещь: если R Squared является большим числом (около 1). Тогда знаменатель формулы VIF станет небольшим числом (поскольку знаменатель равен 1-R в квадрате)

Если знаменатель представляет собой небольшое число, то значение VIF будет большим числом (поскольку мы делим 1 на знаменатель, т.е. 1 - R в квадрате).

Итак, R в квадрате пропорционален VIF.

Например,

Ранее мы получили высокое значение VIF, равное 6,67, поскольку у нас было высокое значение R-квадрата (0,85).

Если бы у нас было низкое значение R Squared, например 0,2, тогда наш VIF был бы низким, как-

VIF = 1 /(1-0,2)

ВИФ = 1/0,8

ВИФ = 1,25

Косвенно это означает, что-

• Если VIF имеет низкое значение, это означает, что другие переменные-предикторы вместе не могут должным образом объяснить дисперсию и установить стабильную связь с указанной нами переменной ответа. Другими словами, «Переменная ответа является статистически независимой или изолированной».
• Если VIF является большим числом, это означает, что другая предикторная переменная вместе в некоторой степени способна объяснить дисперсию и установить стабильную связь с указанной нами переменной ответа. Другими словами, «переменная ответа статистически не является полностью независимой».
• Нам нужно использовать ту же процедуру, что и для «Возраст», чтобы найти VIF всех других независимых переменных. Обычно значение VIF больше 5 не считается хорошим.

Эмпирическое правило для интерпретации фактора инфляции дисперсии:

• 1 = нет корреляции.
• От 1 до 5 = корреляция умеренная.
• Больше 5 = высокая корреляция.

Учтите, что мы получили VIF для каждой переменной, как указано в таблице-

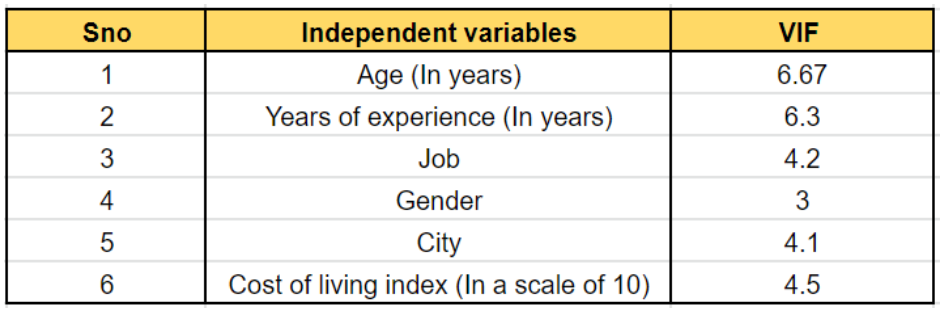
Совершенно очевидно, что «Возраст» и «Количество лет опыта» сильно завышены и коррелированы, поскольку их значение выше 5.

Следовательно, мы можем удалить одну из этих переменных из этой модели (предпочтительно мы можем удалить «Возраст», так как на данный момент он имеет самый высокий VIF). Итак, после удаления «Возраст» количество независимых переменных сократилось с 6 до 5.

Мы можем повторить вышеупомянутый процесс еще раз-

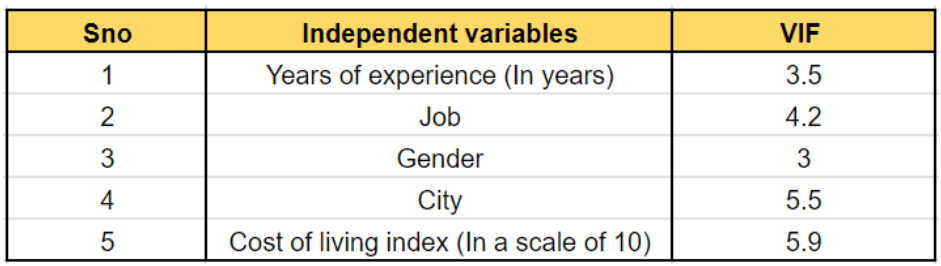
Теперь мы видим, что VIF многолетнего опыта снизился. Кроме того, город и стоимость жизни кажутся завышенными. Следовательно, мы можем исключить одну из этих переменных из модели. В следующей итерации моделирования мы получили значения VIF, как показано ниже: "/>

Теперь все переменные выглядят некоррелированными и независимыми. Следовательно, мы можем приступить к фактическому моделированию, используя «Зарплату» в качестве целевой переменной.

Мы начали с 6 независимых переменных для регрессионной модели. С помощью VIF мы смогли выявить мультиколлинеарность в данных и выделить 2 переменные для исключения из модели. Теперь наша регрессионная модель будет более обобщенной, точной и менее сложной.

Вывод

Как урок из всей статьи, мы можем обобщить все содержание с помощью следующих пунктов-

• В многомерной регрессионной модели коэффициент инфляции дисперсии (VIF) измеряет мультиколлинеарность независимых переменных.
• Хотя мультиколлинеарность не снижает объяснительную способность модели, она снижает статистическую значимость независимых переменных, поэтому ее обнаружение имеет решающее значение.
• Большой VIF для независимой переменной указывает на сильную коллинеарную связь с другими переменными, которую следует учитывать или учитывать в структуре модели и выборе независимой переменной.

В этой статье мы обсудили одну из самых важных, но основополагающих фундаментальных концепций прикладной статистики. Эта метрика VIF доступна в виде встроенной библиотеки в большинстве языков программирования, ориентированных на науку о данных, таких как Python или R. Следовательно, ее легко реализовать, если вы понимаете теоретическую интуицию. Я добавил ссылки на некоторые дополнительные материалы в раздел ссылок, где вы можете углубиться в сложные расчеты, если вам это интересно.

Ссылки n

• Решения для статистики. (2013). Что такое логистическая регрессия? — Решения для статистики. [онлайн] Доступно по адресу: https://www.statisticssolutions.com/what-is-logistic- регрессия/.
• Джейсон Браунли (2016 г.). Логистическая регрессия для машинного обучения. [онлайн] Мастерство машинного обучения. Доступно по адресу: https://machinelearningmastery.com/logistic-regression-for-machine-learning/.
• ]Рогель-Салазар, Дж. (2017). Наука о данных и аналитика с Python. Бока-Ратон, Флорида: CRC Press, Taylor & Фрэнсис Групп.
• ‌Миллер, Т.В. (2015). Маркетинговые исследования данных: методы моделирования в прогнозной аналитике с помощью R и Python. Река Аппер-Сэдл: Financial Times/Prentice Hall.

---

Оригинал