Понимание векторных вложений для поиска на основе ИИ
29 января 2023 г. <цитата>И попрощайтесь с поиском по ключевым словам
В то время как GPT 3+ или ChatGPT, инжиниринг подсказок легче понять интуитивно. Множество руководств и примеров доступны в Интернете и социальных сетях. Например,
* Передовые практики OpenAI для ускорения разработки * Список запросов ChatGPT
Вложения требуют программирования и менее понятны из-за различного нелогичного поведения в отношении того, как это работает. Но это чрезвычайно мощный инструмент для поиска или использования вместе с существующими текстовыми моделями для различных других возможных вариантов использования.
Вложения, возможно, являются не менее мощным инструментом в наборе инструментов ИИ для моделей инструкций. Благодаря своей способности обрабатывать поиск по разным словам и предложениям или даже по целым языкам. Сосредоточение внимания на поиске соответствующего документа по любому запросу.
Например, его можно использовать для поиска и ответа в документации на английском языке. На английском...
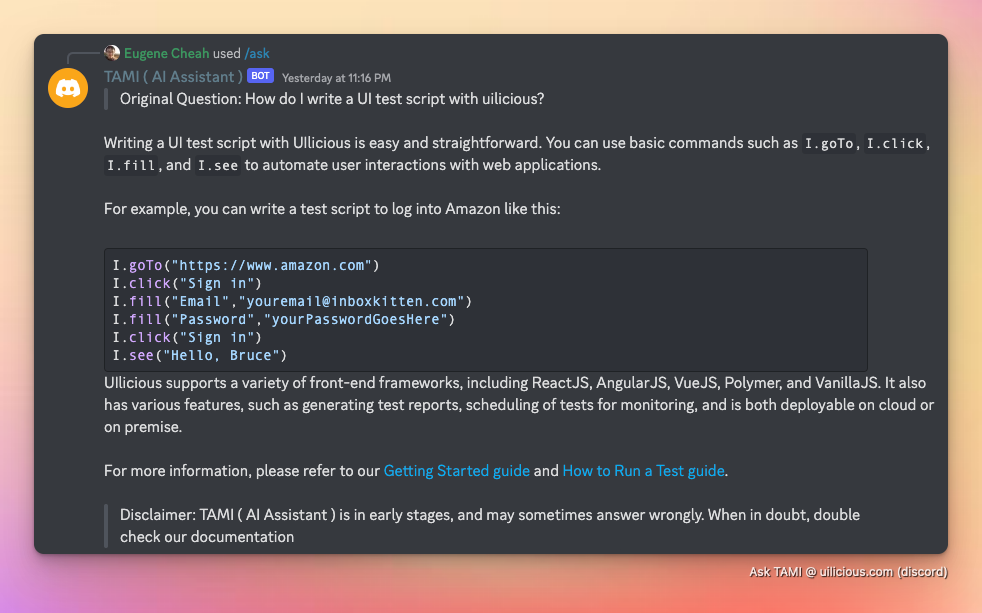
Или японский...
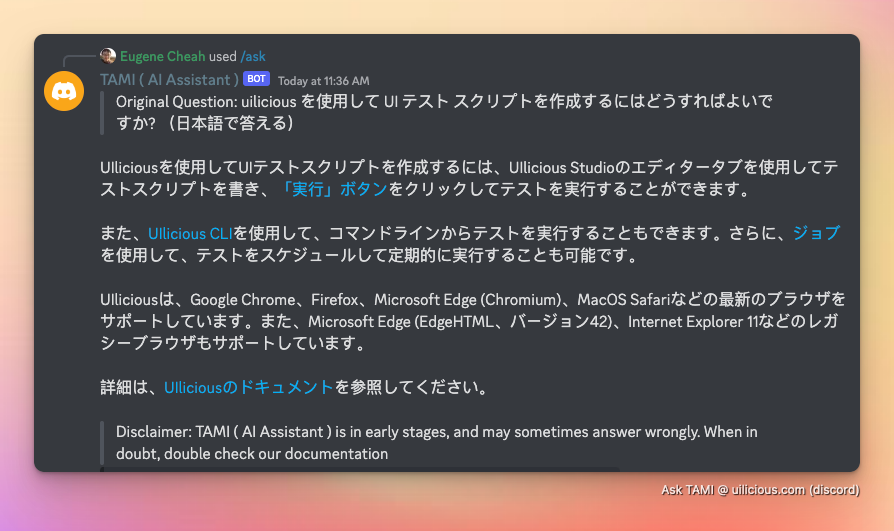
Или любые другие языки, поддерживаемые моделью ИИ.
Встраивание вектора можно использовать для поиска или других задач, таких как ответы на вопросы, классификация текста и создание текста.
:::информация Обратите внимание, что в этой статье основное внимание уделяется аспекту поиска, процесс ответа описан в следующей статье.
:::
Что такое векторное встраивание?
Для создания векторного встраивания используется модель ИИ для встраивания, которая преобразует любой текст (большой документ, предложение или даже слово) в "массив N измерений", называемый вектором.
Например, такое предложение, как Как написать сценарий тестирования пользовательского интерфейса с помощью Uilicious?
Может быть преобразован в массив (называемый вектором) через модель OpenAI text-embedding-ada-002: [0.010046141, -0.009800113, 0.014761676, -0.022538893, ... и более 1000 чисел]
Этот вектор представляет собой обобщенное понимание текста моделью ИИ. Это можно представить как «резюме из N слов», написанное на языке, понятном только ИИ.
Где связанные документы будут находиться на близком расстоянии друг от друга, исходя из понимания ИИ документа (а не только его текста).
Это большой шаг вперед по сравнению с простым поиском по ключевым словам в классических поисковых системах, поскольку он может обрабатывать варианты структуры предложений и языка (при условии, что модель ИИ обучена понимать указанный язык).
Возьмем следующий пример в качестве гипотетического примера, неточно упрощенного до двухмерного пространства, чтобы его было легче понять:

Что можно визуально представить в 2D-пространстве следующим образом.
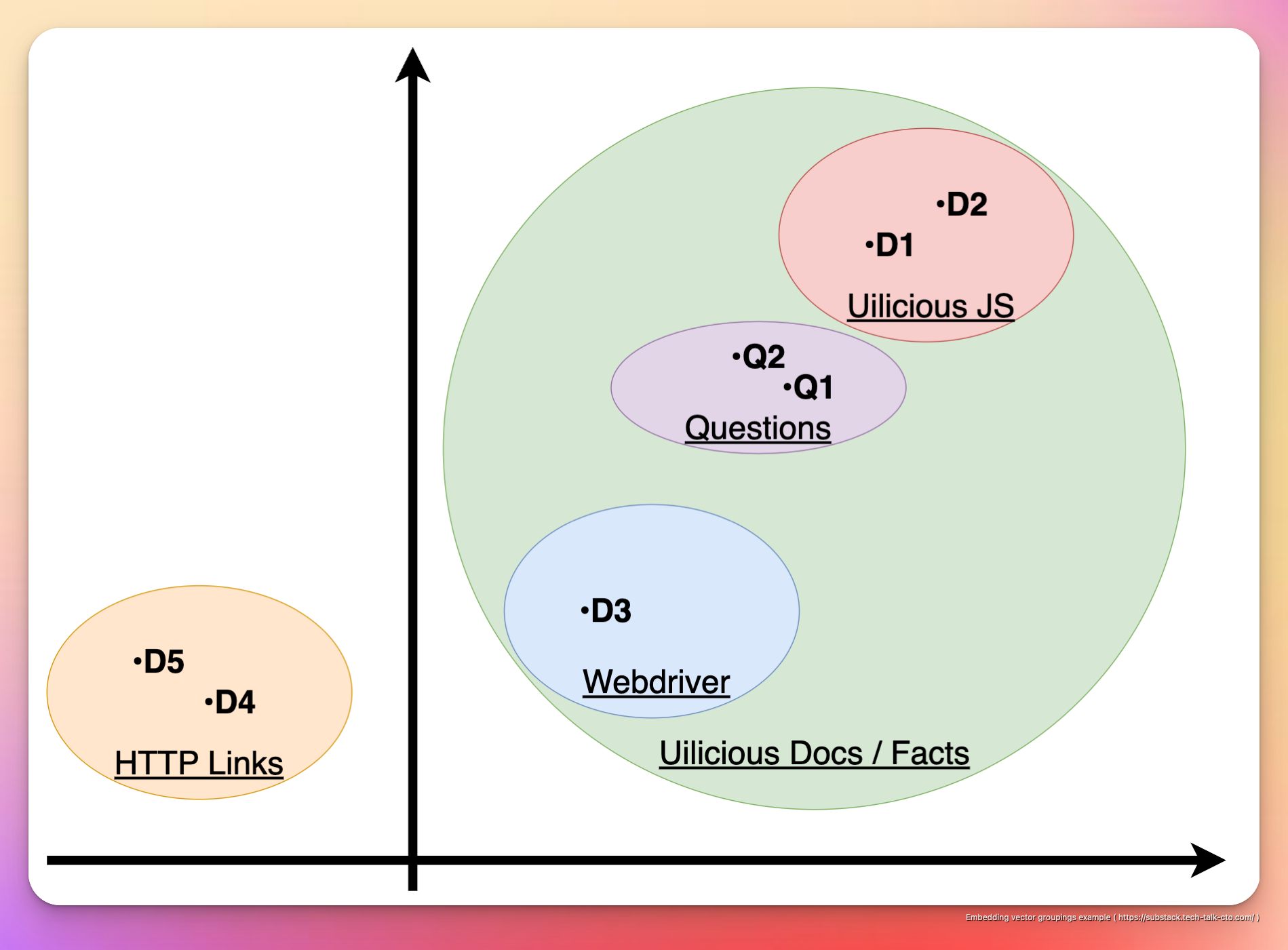
Например, D1,2,3 — это все документы, связанные с тем, как использовать Uilicious различными способами, и они сгруппированы в один кластер
D4 и D5, будучи просто ссылками и не имея никакой собственной ценности, сгруппированы отдельно в другом кластере.
Кроме того, D1 & D2 дополнительно сгруппированы, так как они относятся к Uilicious командам тестирования, использующим наш собственный язык тестирования на основе JavaScript.
В то время как D3 сгруппирован отдельно, так как он касается непосредственного использования протокола веб-драйвера в нашей инфраструктуре, который предназначен для другого варианта использования и аудитории.
Точно так же для Q1 и Q2, несмотря на существенные различия в структуре предложения и языке, поскольку это по существу один и тот же вопрос, два вопроса сгруппированы вместе.
Кроме того, хотя вопрос технически может быть интерпретирован в обоих направлениях (с использованием тестового сценария Uilicious или протокола веб-драйвера), поскольку вопрос подразумевает использование тестового сценария Uilicious поверх веб-драйвера, его расположение «ближе» к D1 & D2 и дальше от D3.
Таким образом, несмотря на огромное совпадение ключевых слов, эти нюансы в группах улавливаются ИИ, закодированным во встраиваниях. Подчеркивая его отличительные отличия от поиска по ключевым словам
:::информация В действительности, однако, вместо упрощенного двухмерного массива, который легко понять людям, вложение может легко быть массивом из 1000+ измерений. Этот массив уникален для конкретной используемой модели ИИ, и его нельзя смешивать с вложениями другой модели ИИ.
:::
Примечания по математике: N-мерная математика несовместима с 2/3D-математикой
Несмотря на то, что упрощенные примеры с двумя измерениями хороши для понимания высокоуровневой концепции группирования относительно одного вопроса (или одной точки зрения), они не точно представляют N-измерения.
Из-за сложной математики размерности N у вас могут возникнуть ситуации, когда A может быть близок к B, B может быть близок к C, но A и C можно считать далекими друг от друга. Это крайне нелогичная ошибка.
Такие расстояния полезны только при использовании относительно одной и той же точки и используемых формул. Который можно рассчитать либо с помощью
* Евклидово расстояние: также известное как теорема Пифагора о стероидах, это наиболее распространенная метрика расстояния. используется и представляет собой расстояние по прямой линии между двумя точками в N-сфере. * Подобие косинуса: это мера углового расстояния между двумя точками на N-сфере. и полезен для измерения сходства документов или других векторов. * Манхэттен или Хемминга Расстояние: эти два показателя используются для измерения различий между двумя векторами и полезны для измерения «расстояние редактирования» между двумя строками.
:::информация Хотя эффективность каждой формулы имеет свои плюсы и минусы для разных вариантов использования. Для текстового поиска общепринято, что евклидово расстояние "работает лучше" в большинстве случаев и "достаточно хорошо" в тех случаях, когда другие методы проигрывают.
:::
Все это фактически используется для уменьшения N-измерений до одного измерения (расстояния) относительно одной точки. В результате это будет означать, что группировка может радикально измениться в зависимости от заданного вопроса.
Этот "относительный" характер расстояний делает классические индексы поиска в базе данных неэффективными.
Если это не имеет смысла, вот как правильно визуализировать 4-мерное пространство с помощью математических N-сфер.

А теперь представьте 1000 измерений? Да и смысла нет.
Так что, не умаляя эту тему диссертацией, я резюмирую, что просто доверяю профессорам математики.
Все, что нам нужно понять, это то, что чем ближе расстояние между двумя точками встраивания векторов, тем выше вероятность того, что они релевантны друг другу.
С точки зрения практической реализации. Сначала начните с использования евклидова расстояния. Прежде чем рассмотреть возможность использования других формул, которые настраиваются методом проб и ошибок для достижения лучших результатов в вашем случае использования (не рекомендуется).

Поиск вложений в базе данных векторов
Поскольку мы можем преобразовывать различные документы во вложения, теперь мы можем хранить их в базе данных и выполнять поиск по ней.
Однако, в отличие от поиска в базе данных SQL с текстом, как поиск, так и искомые данные представляют собой векторное встраивание. Это означает, что традиционные индексы поиска в базе данных неэффективны, когда речь идет о поиске вложений.
Мы можем встроить все ваши документы, предварительно вычислить их и сохранить в базе данных векторного поиска. Который затем можно использовать для предоставления списка совпадений, ранжированных по ближайшему расстоянию.
Это можно сделать с помощью существующих векторных баз данных, таких как
- REDIS: популярная база данных с открытым исходным кодом, которую можно использовать для хранения векторных изображений и поиска. их эффективно.
- Annoy: библиотека, созданная Spotify, которая использует оптимизированный алгоритм для быстрого поиска встраивания.
- FAISS: библиотека, созданная Facebook, которая предоставляет эффективные алгоритмы поиска для больших наборов данных.
Важно отметить, что векторный поиск "база данных" появился относительно недавно. Где подавляющее большинство баз данных векторного поиска были разработаны для вариантов использования, найденных в таких компаниях, как Facebook, Spotify или Google, с наборами записей размером в миллионы или миллиарды. И может быть не оптимизирован для небольших наборов данных.
:::информация В ближайшие несколько лет эта область будет постоянно меняться, вот github 'awesome-list', который поможет отслеживать и найти будущие базы данных поиска векторов
:::
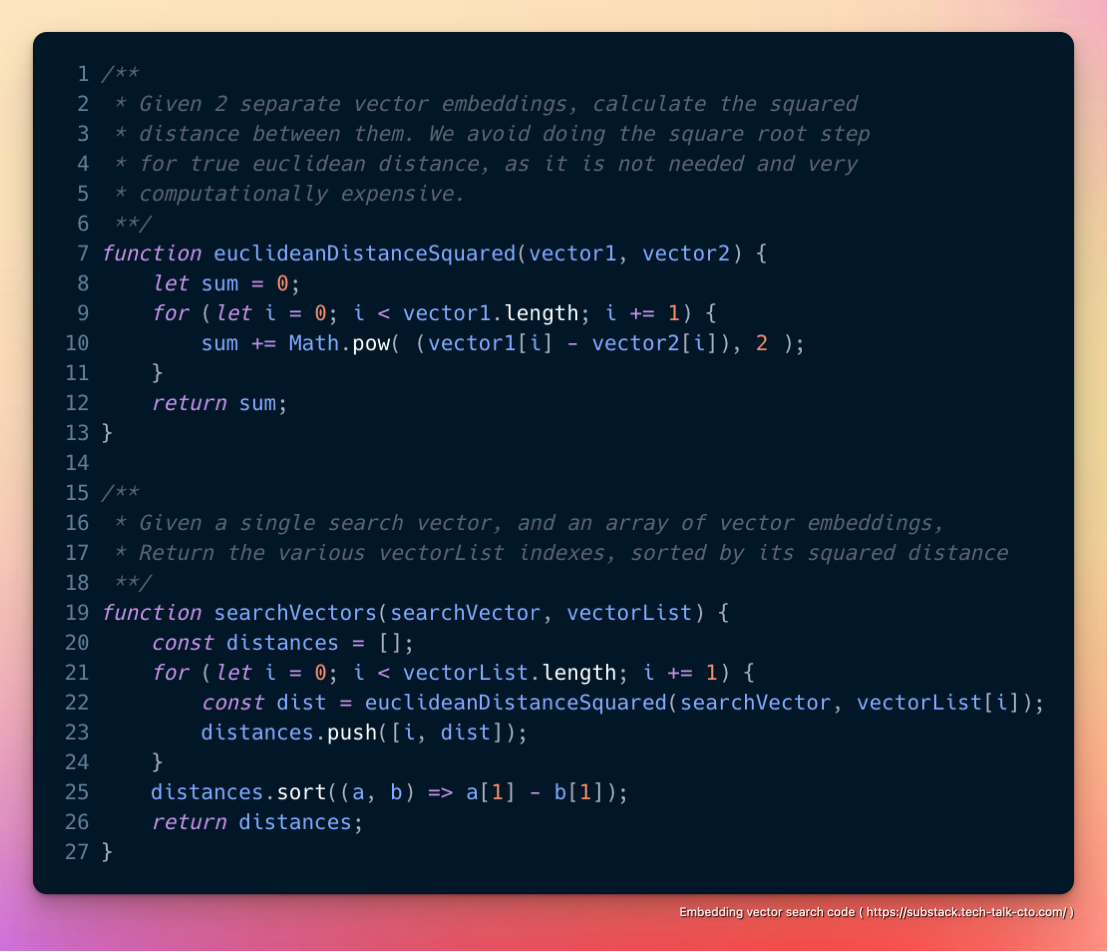
Таким образом, в целом, мы обнаружили, что для небольших наборов данных (< 10 000 ~ 100 000 вложений) хранение набора данных для встраивания в памяти и грубая форсировка квадрата евклидова расстояния «достаточно хороша» для многих случаев использования и когда-нибудь превзойдет формальные решения для баз данных (которые будут иметь накладные расходы на диск/сеть) с чем-то вроде следующего.
Очевидным недостатком этого подхода является то, что весь набор данных должен быть достаточно небольшим, чтобы поместиться в память без дополнительных затрат.
Независимо от того, используете ли вы локальный встроенный поиск в памяти или формальную базу данных векторного поиска.
Все!
Встроенный поиск — это всего лишь алгоритм сортировки и ранжирования, который гибко работает с различными языками и сценариями. Вопрос для вас, как читателя, заключается в том, как вы можете его использовать. Его можно использовать как возможную замену поиска Google или вместе с другими инструментами, от чата до игр. Возможности безграничны и открыты для изучения.
~ До новых встреч 🖖 живите долго и процветайте
Юджин Чеа @ tech-talk-cto.com
Первоначально опубликовано на: https://substack.tech-talk-cto.com/ p/introduction-ai-embeddings-and-how n
Все используемые изображения с указанием их авторства
- Человек в увеличительном стекле от Мартен Ньюхолл в Unsplash
- Зак Галифианакис Математический мем
- Файловые ящики от Ян Антонин Колар в Unsplash
- Большие обои мечты автора Рэнди Тарампи в Unsplash
Оригинал