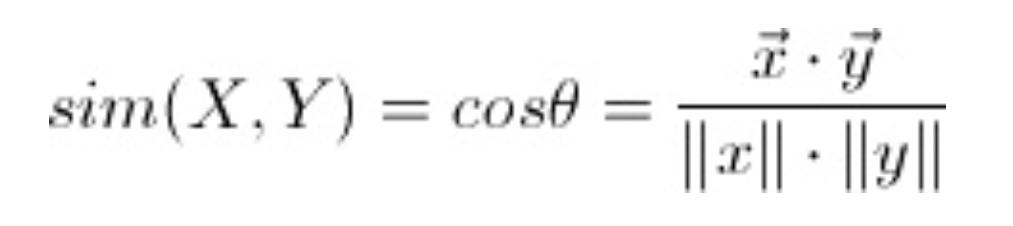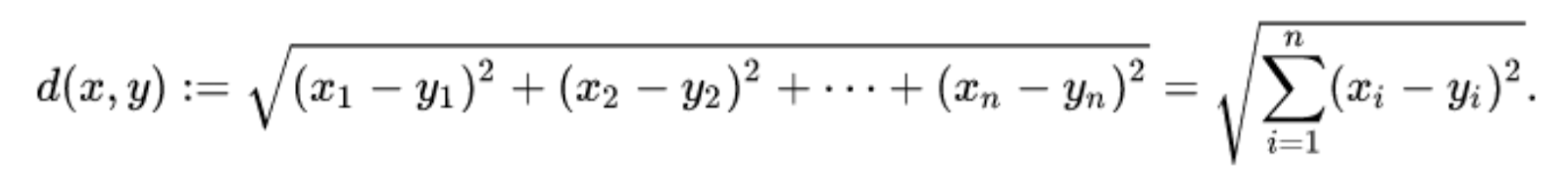
Понимание двухбашенной модели в системах персонализированных рекомендаций
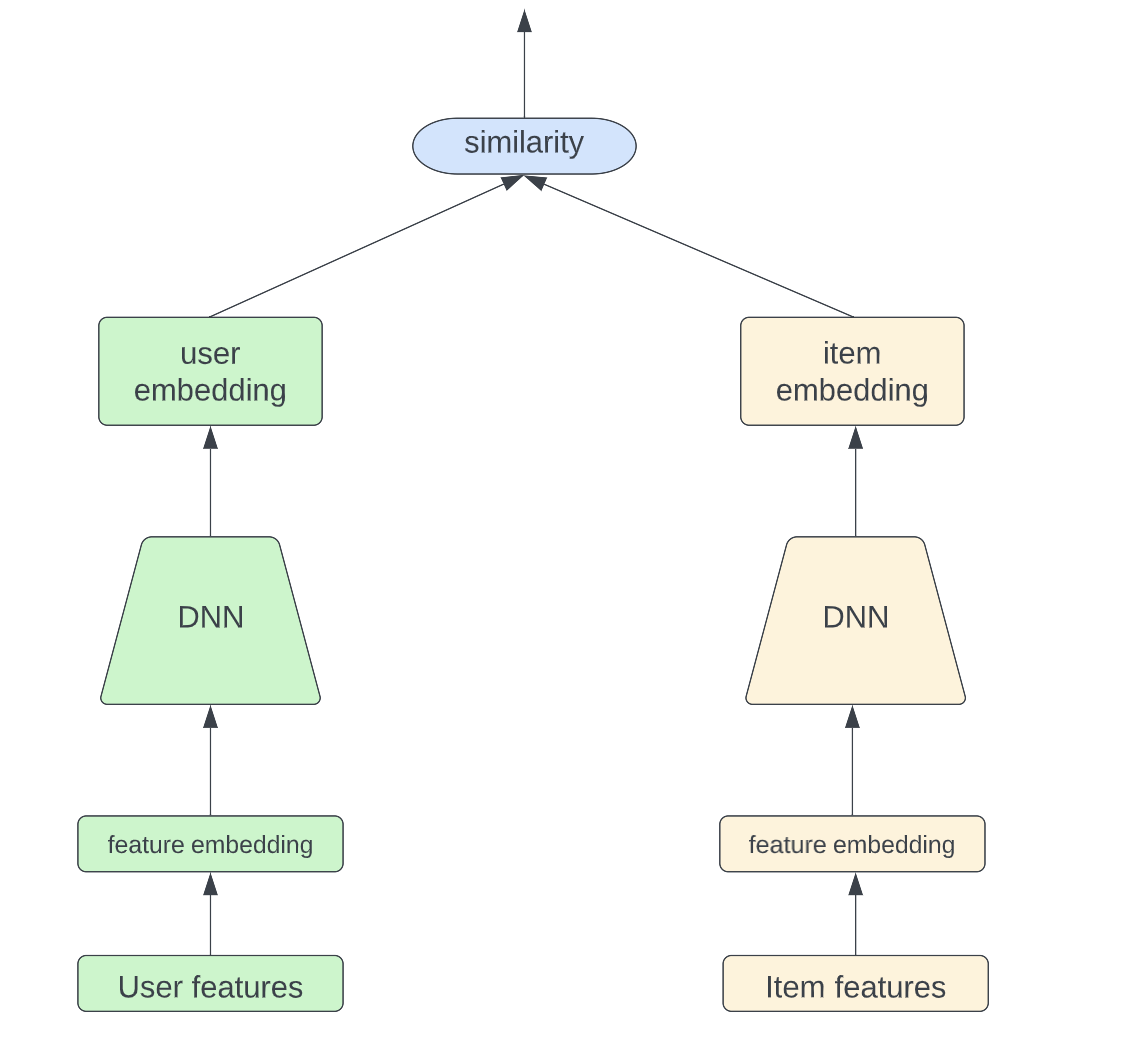
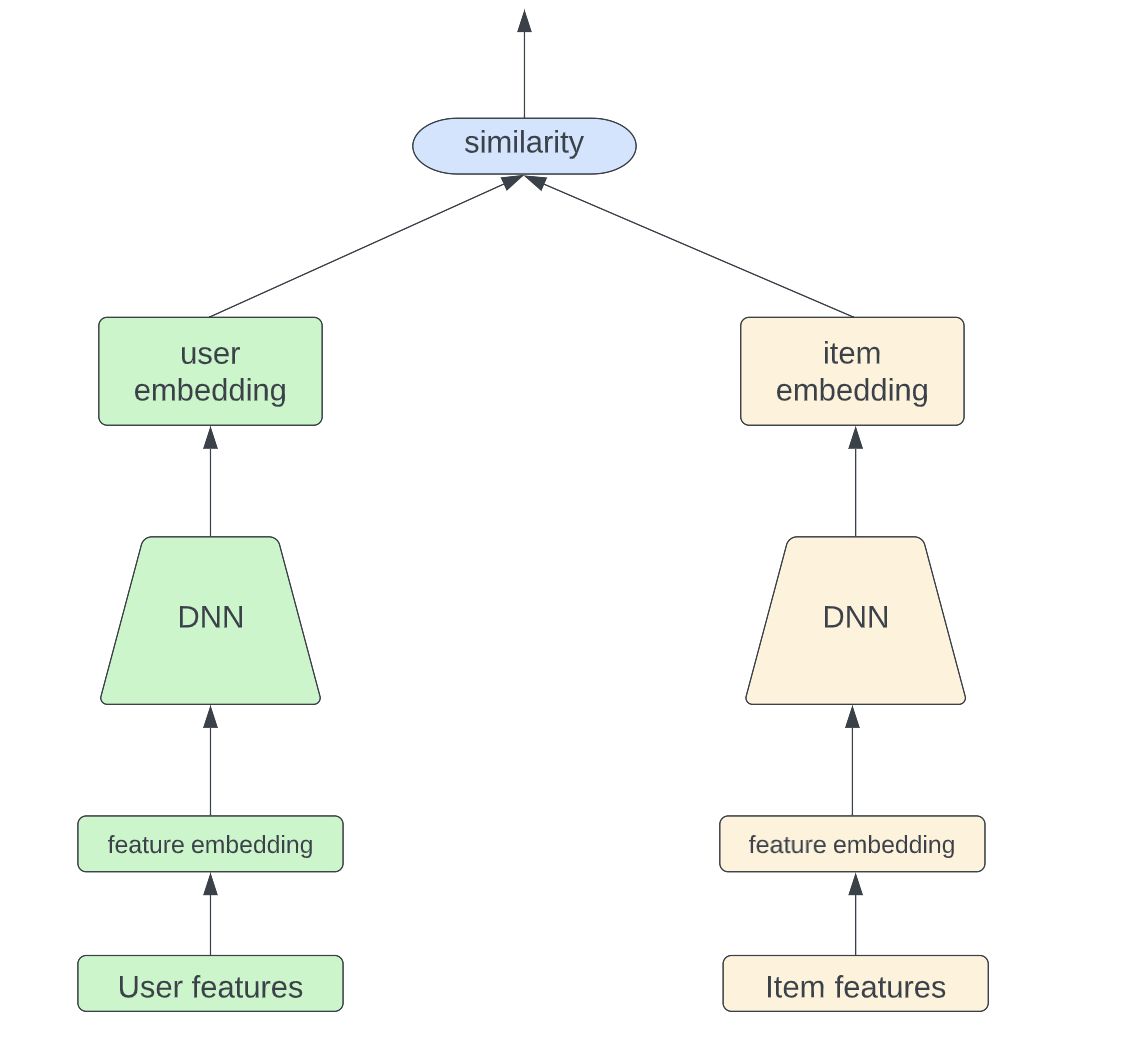
9 января 2023 г.В настоящее время модель двух башен широко используется на этапе поиска системы рекомендаций. Идея для этой архитектуры модели довольно проста; он состоит из двух полностью разделенных башен, одной для пользователя и одной для предмета, как показано на рисунке ниже. Благодаря глубоким нейронным сетям модель способна изучать абстрактные представления высокого уровня как для пользователя, так и для элемента с прошлыми взаимодействиями пользователя с элементом. Результатом является сходство между внедрением пользователя и внедрением элемента, которое показывает, насколько пользователь заинтересован в данном элементе.
Для дальнейшего ускорения онлайн-обслуживания пользовательские внедрения и внедрения элементов могут быть предварительно вычислены и сохранены в автономном режиме. Таким образом, нам нужно только вычислить сходство между пользователями и элементами, внедренными во время онлайн-обслуживания.
Косинусное сходство и евклидово сходство — два наиболее распространенных способа определить сходство между двумя вложениями:
- Косинусное сходство
* Евклидово подобие
В чем точная разница между этими двумя и как мы можем выбрать один из другого?
Теоретически косинусное сходство находится в диапазоне [-1,1], где чем выше число, тем более похожи два входа. Поскольку, когда косинусное сходство равно 1, угол между входными данными равен 0 градусов, однако, когда косинусное сходство равно -1, угол между входными данными составляет 180 градусов, что означает, что два вектора находятся в двух совершенно разных направлениях.
В то время как для евклидова подобия выход находится в диапазоне [-∞, +∞]. Чем ближе результат к 0, тем более похожи входные данные.
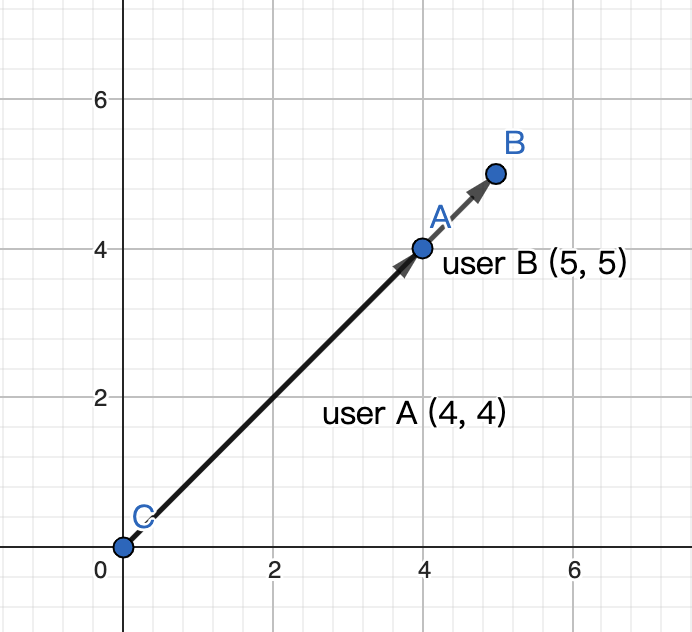
Самое большое отличие состоит в том, что подобие косинуса нечувствительно к абсолютному расстоянию в пространстве, имеет значение только разность направлений. Что это значит? Давайте используем один пример для иллюстрации. Допустим, у нас есть пользователь А, который оценивает 2 фильма как (4,4), и пользователь Б, который оценивает 2 хода как (5,5). Если мы вычислим косинусное сходство и евклидово сходство отдельно для этих двух пользователей, очевидно, что косинусное сходство равно 1, а это означает, что между этими двумя пользователями нет разницы. Однако евклидово сходство равно 1,4, что означает, что пользователь A и пользователь B все еще отличаются друг от друга. Таким образом, евклидово сходство является более строгим, чем косинусное сходство, потому что евклидово сходство требует не только того, чтобы у пользователей были одинаковые вкусы в отношении фильмов, но и одинакового уровня «нравится» для каждого фильма.
Однако что, если у разных пользователей разные шкалы рейтинга? Например, пользователь А ставит оценку (3,3), а пользователь Б ставит оценку (4,4). Пользователь А имеет довольно строгую планку при оценке, и наивысшая оценка для этого пользователя равна 3, в то время как у пользователя Б очень слабая планка при оценке, и пользователь дает 5 более чем 80% рекомендуемых фильмов. В этой ситуации интуитивно понятно, что пользователю А очень нравятся эти 2 фильма, однако на самом деле они не нравятся пользователю Б. Но косинусное сходство не может этого отразить. Чтобы откалибровать косинусное сходство, мы можем ввести коэффициент корреляции Пирсона, где мы используем среднюю оценку пользователя для калибровки каждой оценки, выставленной пользователем.
В приведенном выше примере предположим, что средний балл пользователя А равен 2, а средний балл пользователя Б равен 5. Для калибровки мы вычитаем средний балл пользователя, рассчитанный на основе прошлого поведения, из каждого измерения. Затем после калибровки пользователь А будет (1,1), а пользователь Б будет (-1,-1). Теперь косинусное сходство между этими двумя пользователями равно -1, что указывает на то, что это два совершенно разных пользователя. Существует также другой способ расчета коэффициента корреляции Пирсона.
Вместо калибровки на уровне пользователя мы могли бы также выполнить калибровку на уровне элемента. Допустим, пользователь А ставит оценку (3,3), а пользователь Б ставит оценку (4,4). И у нас есть 1000 пользователей, которые поставили оценки этим двум фильмам, и средний балл для обоих фильмов составляет 3,5. Если мы вычтем рейтинг каждого элемента, данный пользователем, из среднего балла элемента, рассчитанного по 1000 пользователям, мы получим пользователя А как (-0,5,-0,5) и пользователя Б как (0,5,0,5), что также показывает, что пользователь А и пользователь B на самом деле очень разные пользователи, так как их сходство равно -1.
Оригинал