
Понимание модели линии крыши
23 декабря 2023 г.Нельзя отрицать тот факт, что производительность нашего кода имеет большое значение. Для бесчисленных приложений, включая моделирование HPC, игры, графику и т. д., производительность означает не только более быстрое выполнение и меньшее время ожидания. Это также напрямую связано со стоимостью, потреблением энергии и пользовательским опытом. Более производительный код часто экономит много вычислительных ресурсов, что потенциально приводит к мерам по сокращению затрат, особенно при работе на суперкомпьютерах и центрах обработки данных.
Однако путь к повышению производительности может оказаться сложной задачей, требующей стратегического подхода. Прежде чем повышать производительность, важным первым шагом является определение теоретических пределов достижимой производительности. Это гарантирует, что программист знает, к чему он стремится и насколько далеко он может зайти в оптимизации производительности.
Именно здесь такие модели производительности, как модель с линией крыши, становятся путеводным маяком. Предоставляя представление о теоретических пределах производительности и выявляя узкие места, модель линии крыши становится бесценным инструментом для достижения совершенства в вычислениях, позволяя разработчикам принимать обоснованные решения по стратегиям оптимизации производительности.
В этой статье я углублюсь в то, что такое модель линии крыши. Мы также рассмотрим подробный пример, чтобы продемонстрировать, как определить, является ли наш алгоритм вычислительным или привязанным к памяти. Модель линии крыши позволяет нам определить, работает ли наш алгоритм на пике своего потенциала или требует дальнейшего улучшения.

Линии крыши
Теоретические пределы (или линии крыши) обусловлены главным образом архитектурой машины и характеристиками памяти. Как обсуждалось ранее в моем блоге о необходимости параллелизма, это зависит от программисту использовать возможности оборудования для максимальной производительности алгоритма.
Два основных верхних предела (или линии крыши) достижимой производительности:
- Максимальная производительность
- Пропускная способность/пропускная способность памяти
- Этот ЦП может одновременно выполнять 4 операции с плавающей запятой двойной точности (8 байтов) (т. е. векторизуется).
Пиковая производительность [операций/с]
Применимая пиковая производительность зависит от вычислительных ресурсов, доступных на оборудовании. На это влияют различные архитектурные факторы, такие как тактовая частота процессора и реализация конвейерной обработки.
Эта линия крыши также зависит от типов операций, которые выполняет наш код. Например, линии крыши могут различаться для одного кода с операциями слитого умножения и сложения (FMA), а для другого — с базовыми арифметическими операциями. Возможность алгоритма использовать векторизацию или SIMD также повлияет на его производительность.
Пропускная способность/пропускная способность памяти
Еще один потолок связан с тем, что между памятью и процессором можно передавать только ограниченный объем данных.
Эта линия крыши зависит от двух аспектов: зависимой от кода интенсивности вычислений (или арифметических или операционных) [операций/байт] и аппаратно-зависимая пиковая пропускная способность [байт/с].
Что такое интенсивность вычислений?
Интенсивность вычислений определяет количество байтов, передаваемых между памятью и ЦП для каждой операции с плавающей запятой в алгоритме. Проще говоря, это отношение общего количества операций с плавающей запятой в вашем алгоритме к количеству переданных байтов. Таким образом, измеряется как операций/байт.
А как насчет пиковой пропускной способности памяти?
Современные компьютеры имеют сложную иерархию памяти. Высокоуровневое представление иерархии памяти показано ниже:
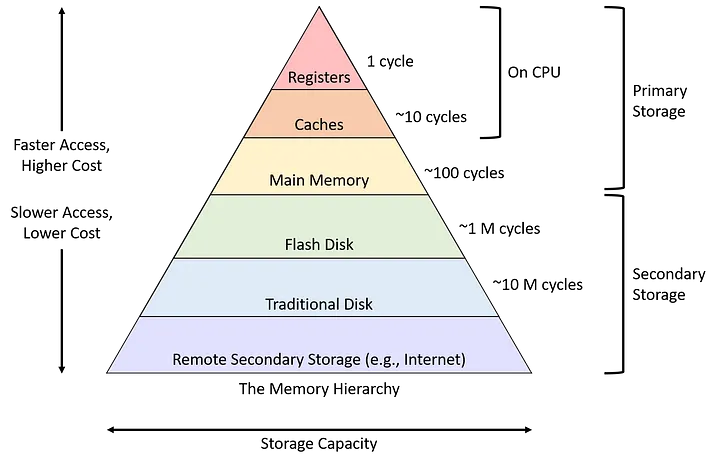
Существует несколько уровней кэша данных (в основном от L1 до L3), за которыми следует DRAM. Пропускная способность памяти каждой из этих воспоминаний значительно различается. В то время как кэш-память уровня 1 (L1) имеет самую высокую пропускную способность памяти, DRAM имеет самую низкую. Однако емкость L1 существенно мала (в современных процессорах персональных компьютеров она составляет порядка КБ). Напротив, DRAM может быть значительно больше (порядка нескольких ГБ).
Для определения пиковой пропускной способности памяти можно использовать набор тестов, таких как тест STREAM.
Модель крыши Naive
Обсудив основы, давайте перейдем к тому, как мы используем всю эту информацию для оценки нашей максимальной производительности.
Простая модель линии крыши (так называемая наивная модель линии крыши) может быть представлена как:
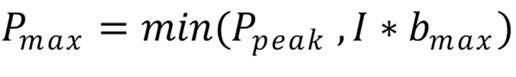
Pₘₐₓ: верхняя граница производительности [операций/с]
Машинно-зависимые параметры:
Pₚₑₐₖ: применимая пиковая производительность [операций/с]
bₘₐₓ: допустимая пиковая пропускная способность [байт/с]
Параметр, зависящий от кода:
I: интенсивность вычислений [операций/байт]
Как обсуждалось выше, узким местом может быть выполнение работы (Pₚₑₐₖ) или путь к данным (I*bₘₐₓ).
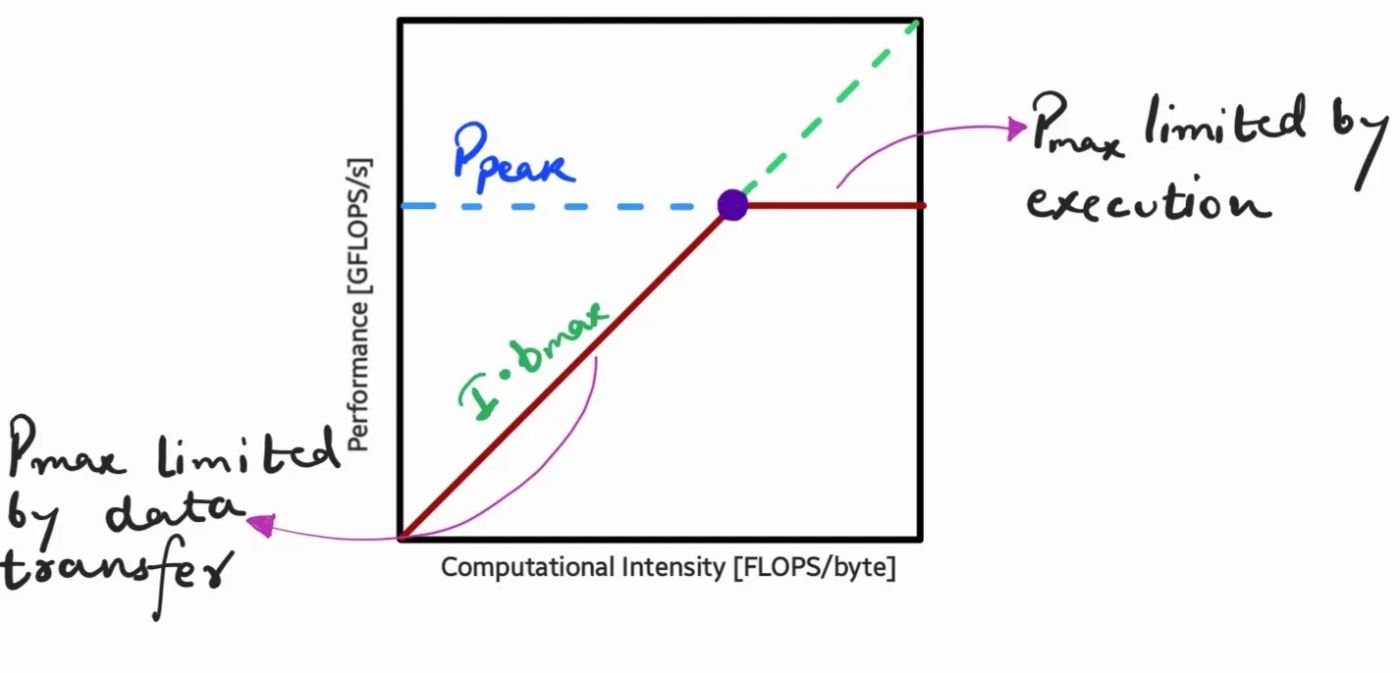
Предположения, лежащие в основе модели
Несколько важных факторов способствуют простоте и эффективности модели линии крыши.
Прежде всего, модель предполагает идеальный сценарий, в котором передача данных и выполнение ядра полностью перекрываются, что подчеркивает важность плавной координации между этими двумя аспектами вычислений.
<блок-цитата>Модель работает по принципу, что самый медленный ограничивающий фактор, будь то выполнение ядра или передача данных, определяет общую производительность. В этом соревновании «победителем» становится фактор, оказывающий наиболее значительное влияние, в то время как предполагается, что влияние других факторов незначительно.
Примечательно, что эффекты задержки не учитываются, что подразумевает предположение об идеальном режиме потоковой передачи, в котором передача данных уже идет.
Наконец, модель ориентирована на «стационарное» выполнение кода, исключая эффекты свертывания и свертывания и предполагая работу всего конвейера, что еще больше упрощает ее.
Несмотря на свою простоту, модель «линия крыши» оказывается весьма эффективной, поскольку отражает эту сложность и предлагает практический инструмент для общения между экспертами в области высокопроизводительных вычислений (HPC) и исследователями приложений.
Усовершенствованная модель крыши
Модель крыши Naive можно дорабатывать и улучшать разными способами. Во-первых, добавление нескольких линий крыши для различных арифметических операций может улучшить модель линии крыши.
Аналогично, использование разной пропускной способности памяти для разных доступных памятей делает модель более выразительной.
Пример показан ниже:
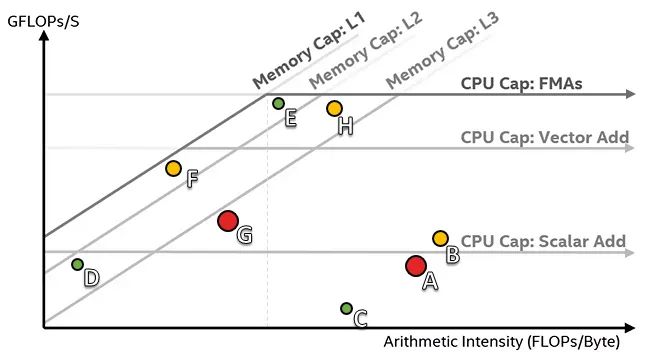
При проведении теоретических расчетов (что мы и сделаем очень скоро) модель линии крыши Naïve не учитывает эффекты задержки. Однако, если у нас есть достаточно информации, мы можем включить в наши расчеты эффекты задержки, улучшив наши прогнозы.
Модель крыши в действии
Давайте воспользуемся тем, что мы узнали выше, чтобы применить модель линии крыши к реальной проблеме.
Этот пример основан на моих знаниях, полученных во время изучения одного из моих любимых курсов в Мюнхенском техническом университете: продвинутое программирование TUM SCCS.
Моя машина имеет одноядерный процессор с частотой 2 ГГц (довольно старый, правда?) и следующими характеристиками:
<блок-цитата>2. Задержка основных арифметических операций (+, -, *) составляет 2 такта (одна операция на два такта).
3. Задержка операции слитого умножения и сложения (a += b * c) составляет 3 цикла.
4. Эти операции не являются конвейерными.
5. Этот ЦП имеет 2 модуля загрузки и 1 блок хранения, каждый из которых может содержать 32 байта (4 двойных значения).
6. Доступ к кэш-памяти является конвейерным и занимает 5 тактов. Кэш работает на частоте 2 ГГц.
7. Доступ к основной памяти не конвейерный и стоит 10 тактов. Основная память работает на частоте 800 МГц.
8. Оба типа памяти могут одновременно загружать 2 векторных регистра (2 × 32 байта) или хранить 1 векторный регистр (32 байта).
9. Предположим, что один блок загрузки/хранения ЦП может загружать/сохранять один векторный регистр.
Учитывая все архитектурные характеристики, мы можем сначала рассчитать аппаратно-зависимые параметры нашей модели.
После этого мы можем просмотреть наш код и приступить к расчетам вычислительной интенсивности.
Расчет применимой пиковой производительности
Теоретическая пиковая производительность будет зависеть от типа операций, которые мы выполняем.
Для основных арифметических операций:
Поскольку ЦП может одновременно выполнять 4 операции с плавающей запятой двойной точности, а задержка основных арифметических операций составляет 2 цикла, теоретическую пиковую производительность можно измерить как:
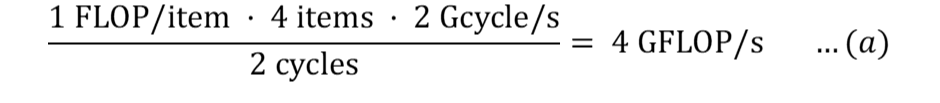
Для операций плавного умножения-сложения (FMA):
Для операций FMA будет 2 FLOP/элемент (сложение + умножение). Однако задержка составляет 3 цикла. Таким образом, теоретическая пиковая производительность составляет:
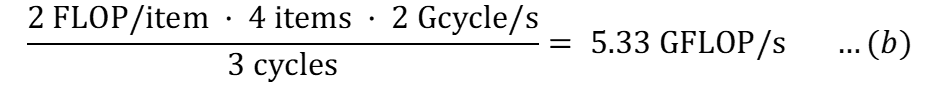
Расчет пропускной способности памяти
К сожалению, расчет применимой пропускной способности памяти немного сложнее. Как обсуждалось выше, разные типы памяти могут иметь разные значения пропускной способности (в зависимости от их размера и близости к процессору). Таким образом, чтобы точно смоделировать линии крыши, важно учитывать как можно больше из них. В нашем примере мы сосредоточимся на кеше и основной памяти.
Теоретическая пропускная способность чтения памяти:
Если пренебречь эффектами задержки из-за соединения с процессором, пропускная способность чтения основной памяти и кэша будет зависеть от их емкости и тактовой частоты.
Оба типа памяти могут либо загружать 2 векторных регистра (2 × 32 байта), либо хранить 1 векторный регистр (32 байта) одновременно (8-я спецификация выше).
Для основной памяти (без эффектов задержки):
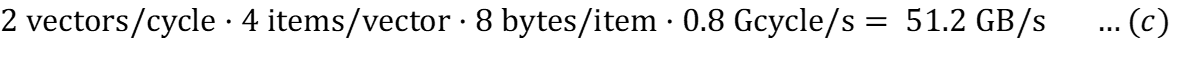
Для кэша (без эффектов задержки):
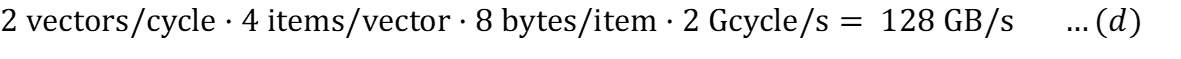
Аналогичные расчеты можно провести и для теоретической пропускной способности записи.
Применимая пропускная способность памяти для чтения/записи:
В любом реальном случае соединение между процессором и памятью (как кэшем, так и основной памятью) приведет к некоторым эффектам задержки.
Из-за этих эффектов ЦП может использовать только часть доступной пропускной способности. Поэтому важно учитывать эти эффекты.
Для чтения из основной памяти (с эффектом задержки):
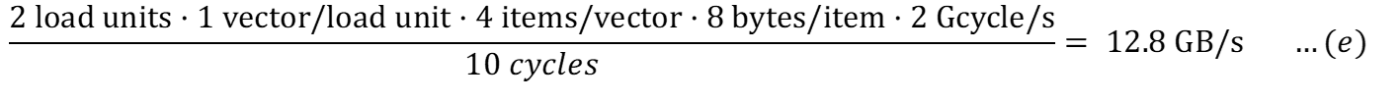
Для записи в основную память (с эффектом задержки):
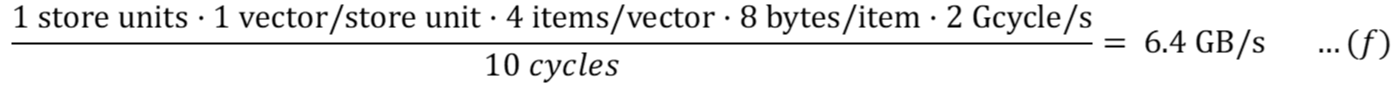
Как указано в спецификациях, доступ к кэш-памяти является конвейерным (6-я спецификация выше). Если конвейер заполнен, эффекты задержки можно игнорировать в наших расчетах.
Для чтения кэша (с конвейерным доступом):
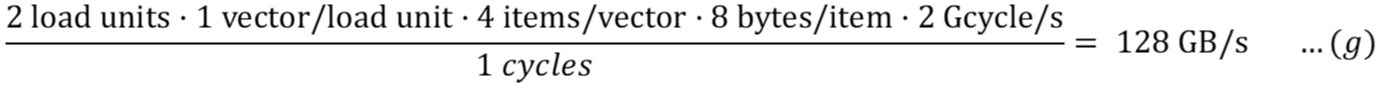
Для записи в кэш (с конвейерным доступом):
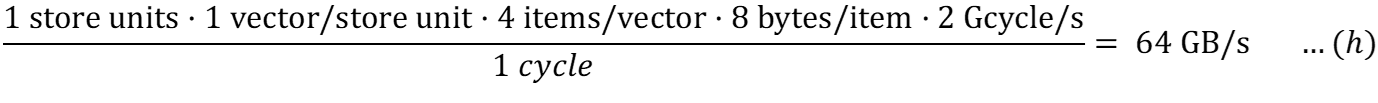
Расчет вычислительной интенсивности
Давайте рассмотрим приложение, в котором основные вычисления включают функцию умножения матрицы на матрицу. Здесь самый внутренний цикл над i вычисляет элемент (row,col) матрицы result, взяв скалярное произведение row-я строка слева с col-м столбцом справа.
Вот полный код:
// result[row,column] = dot_product(left[row, :], right[:, col])
void matrix_mult(size_t rows, size_t columns, size_t k,
double *left, double *right, double *result) {
for (auto row = 0; row < rows; ++row) {
for (auto col = 0; col < columns; ++col) {
for (auto i = 0; i < k; ++i) {
if (i == 0) {
result[row*columns + col] = left[row*k + i] * right[i*columns + col];
}
else {
result[row*columns + col] += left[row*k + i] * ri[i*columns + col];
}
}
}
}
}
Как обсуждалось выше,
<блок-цитата>Интенсивность вычислений определяет количество байтов, передаваемых между памятью и ЦП для каждой операции с плавающей запятой в алгоритме. Проще говоря, это отношение общего количества операций с плавающей запятой в вашем алгоритме к количеству переданных байтов. Таким образом, измеряется как операций/байт.
Начнем с количества операций с плавающей запятой.
Общее количество операций с плавающей запятой:
В общей сложности циклы выполняются rows*columns*k итераций.
Однако для всех i = 0 выполняются только умножения. Таким образом, всего выполняется умножение rows*columns.
Для остальных итераций (которые входят в часть else) выполняются операции FMA (fused-multiply-add). Всего существует (k-1) *rows*columns FMA-операций. Каждая операция FMA состоит из двух операций с плавающей запятой. Таким образом, мы имеем:
Общее количество умножений: строки*столбцы
Всего операций FMA: (k-1)*строки*столбцы
Общее количество операций с плавающей запятой:
(2k-2)*строки*столбцы + строки*столбцы = (2k-1)*строки*столбцы … (i)
Общее количество транзакций в памяти:
Следующий шаг — определение количества байтов, переданных между памятью и процессором.
Это можно рассчитать, определив общее количество транзакций памяти между ними.
<блок-цитата>Примечание. Для упрощения предположим, что (a += b * c) не требует взаимодействия с памятью для промежуточного результата b * c.
Алгоритм включает в себя несколько операций чтения и записи над матрицами левой, правой и результирующей. Чтобы подсчитать общее количество транзакций, нам необходимо учесть все это (и, возможно, больше).
Начнем!
левая матрица считывается на каждой итерации. Таким образом, общая сумма чтений левой матрицы равна rows*columns*k.
Аналогично, правая матрица также считывается много раз.
Это все?
Нет.
Матрица result также считывается для операций FMA (_a =_ **_a_** _+ b * c_). Общее количество чтений составляет rows*columns*(k-1).
Наконец, к матрице result обращаются в общей сложности rows*columns*k раз для операций записи.
Подводя итог:
<блок-цитата>Всего операций чтения:
2*строки*столбцы*k + строки*столбцы*(k-1) = строки*столбцы*(3k-1) … (j)
Всего операций записи:
строки*столбцы*k … (k)
Таким образом, интенсивность вычислений можно рассчитать как:
Для чтения данных:
Использование (i) и (j):
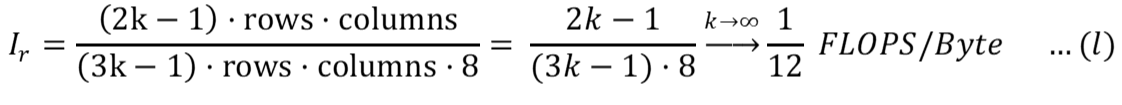
Для записи данных:
Использование (i) и (k):
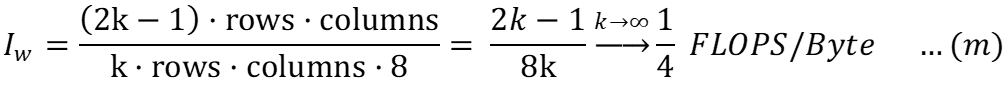
Собираем все вместе
Уф! Мы почти у цели.
Рассчитав все элементы нашей модели линии крыши, давайте соберем все вместе и посмотрим, как работает наш алгоритм и каков ограничивающий компонент системы.
Опять же, мы разбиваем все на два случая.
Когда кеш не задействован
Скорость чтения можно рассчитать, используя интенсивность вычислений, рассчитанную в (l), и применимую пропускную способность чтения для основной памяти в (e):
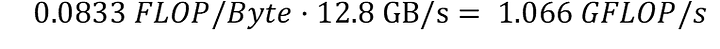
Аналогично, скорость записи можно рассчитать, используя интенсивность вычислений, рассчитанную в (m), и применимую пропускную способность записи для основной памяти в (f):
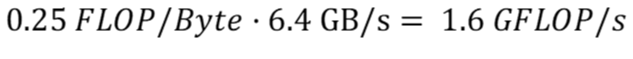
Поскольку в большинстве вычислений во внутреннем цикле используется инструкция плавного умножения-сложения, мы возьмем FMA-пик в качестве пиковой производительности нашего процессора с плавающей запятой для обоих случаев.
Таким образом, используя (b), пиковую производительность нашего алгоритма можно спрогнозировать как:
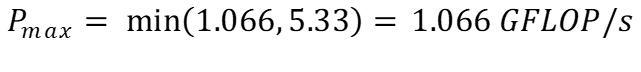
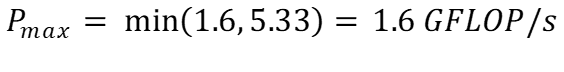
Глядя на эти цифры, ясно видно, что наш алгоритм ограничен памятью. Он может выполнять больше операций с плавающей запятой, но наш процессор не может читать/записывать данные достаточно быстро.
Когда задействован кеш
Скорость чтения можно рассчитать, используя интенсивность вычислений, рассчитанную в (l), и применимую пропускную способность чтения для кэша в (g):
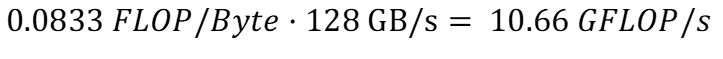
Аналогично, скорость записи можно рассчитать, используя интенсивность вычислений, рассчитанную в (m), и применимую пропускную способность записи для кэша в (h):
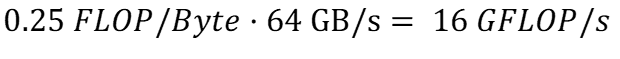
Опять же, используя (b), пиковую производительность нашего алгоритма можно спрогнозировать как:
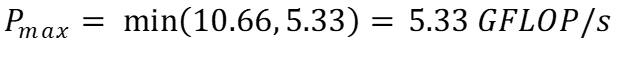
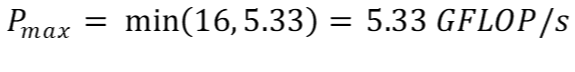
В этом случае алгоритм ограничен вычислениями. Хотя он может быстро получить доступ к данным, у него недостаточно ресурсов для выполнения такого количества операций с плавающей запятой. Таким образом, возможно, нам стоит рассмотреть возможность использования более быстрого процессора для нашего алгоритма!
Заключительные слова
Вот как будет выглядеть наша модель линии крыши:
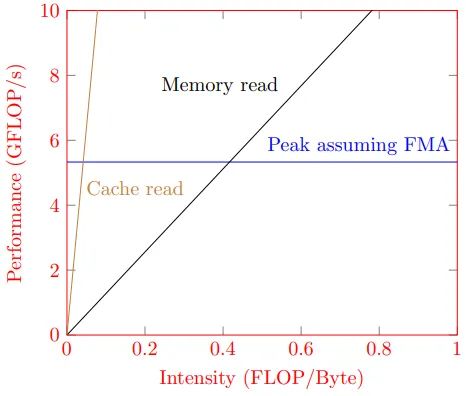
Этот график ясно показывает, какими могут быть теоретические ограничения нашего алгоритма. Зная о них, мы можем тщательно выявить потенциальные узкие места нашего алгоритма и попытаться достичь теоретических пределов.
Точно так же это также помогает нам определить, когда следует прекратить оптимизацию нашего кода, поскольку, возможно, наше оборудование не позволит проводить дальнейшую оптимизацию.
Поскольку современные процессоры становятся более мощными, многие алгоритмы имеют тенденцию быть привязанными к памяти (из-за так называемого «Стена памяти"). Именно по этой причине разработчики вкладывают так много усилий в улучшение шаблонов доступа к памяти.
<блок-цитата>Здесь важно отметить, что анализ линии крыши не всегда требует большого количества ручных вычислений. Существует целый ряд коммерческих и открытых инструментов, которые могут помочь нам создать мощную визуализацию линии крыши. К этим инструментам относятся Empirical Roofline Tool (ERT) — для сбора данных о потолках линии крыши для конкретного оборудования, а также такие инструменты, как LIKWID, Intel® Advisor Roofline и Intel® VTune™ для сбора данных о производительности конкретных приложений.
Надеюсь, эта история помогла вам понять основы и сложности модели линии крыши!

Рекомендуемые ресурсы
[1] Очень короткое введение в модель Roofline — YouTube
[2] Roofline_MuCoSim-SS22.pdf (fau. де)
[3] Модель производительности — HPC Wiki (hpc-wiki.info)
[4] RooflineVyNoYellow.pdf (berkeley.edu)< /п>
[5] Модель линии крыши (cornell.edu)< /а>
[6] Tutorial-ISC2019-Intro-v2.pdf (nersc.gov)
[7] Кафедра научных вычислений (tum.de)
[8] berkeleylab / cs-roofline-toolkit — Bitbucket
:::информация Также опубликовано здесь.
Рекомендованное фото Джошуа Хёне на сайте Unsplash
:::
Оригинал

