Теория когерентного сокращения изменяющихся во времени параметров в VAR: Теория когерентного TVP-VAR

Таблица ссылок

Аннотация и введение

Теория когерентного TVP-VAR

Прогнозирование с помощью TC-TVP-VAR

Анализ ответа в ZLB с TC-TVP-VAR

Заключение и ссылки

Приложение

2 Теория когерентного TVP-VAR

Построение согласованной теории-априорной модели основывается на идее, что экономическая теория подразумевает ограничения на параметры TVP-VAR. Интуитивно мы можем обнаружить эти ограничения, указав априорное распределение на глубоких параметрах из теории, смоделировав данные из теории, а затем оценив TVP-VAR на смоделированных данных. Наложение априорной модели на глубокие параметры из теории затем вызовет априорную модель на параметры TVP-VAR, кодирующие ограничения, налагаемые экономической теорией. Основываясь на этой идее, в этом разделе я аналитически вывожу априорную модель для TVP-VAR, которая является согласованной теорией в том смысле, что она центрирует изменяющиеся во времени коэффициенты на ограничениях перекрестных уравнений, подразумеваемых базовой экономической теорией относительно переменных в системе.

ОбозначениеПрежде чем двигаться дальше, я представлю некоторые соглашения об обозначениях, используемые в статье. Скаляры указаны строчными буквами и нормальным шрифтом. Векторы указаны строчными буквами и жирным шрифтом. Матрицы указаны заглавными буквами и жирным шрифтом.

2.1 Построение предшествующего

TVP-VAR определяется по формуле:

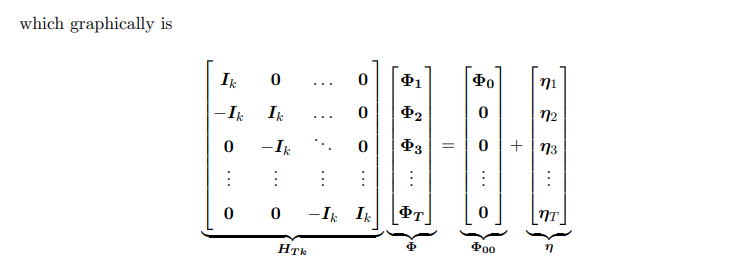
2.2 Моделирование предшествующего

2.3 Условная апостериорная функция Φ и Σu

2.4 λ, γ и компромисс между сложностью подгонки

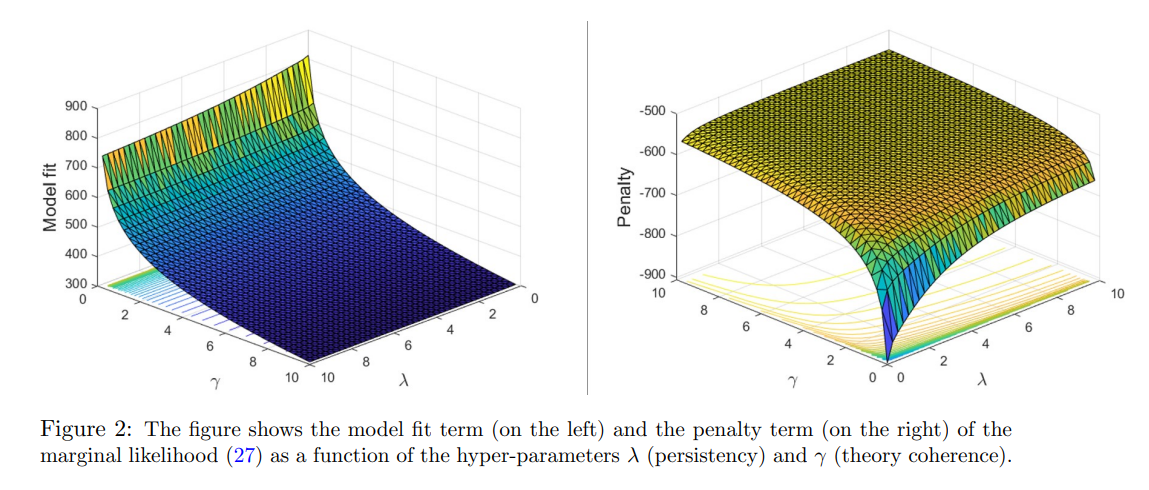
Настройка оптимальной степени согласованности теории и внутреннего количества временных вариаций коэффициентов является деликатным вопросом, поскольку она явно подразумевает компромисс между сложностью подгонки. Фактически, очень низкие значения как γ, так и λ априори подразумевают, что коэффициенты в двух последовательных периодах времени могут потенциально сильно отличаться друг от друга и быть далеки от функций ограничения, определенных теорией.16 Интуитивно понятно, что эта модель будет очень хорошо подгонять данные в выборке, но будет плохо работать для прогнозирования вне выборки. Действительно, уменьшение γ и λ в целом увеличит подгонку модели в выборке за счет точности вне выборки. Основываясь на этом аргументе, я рекомендую основывать оптимальный выбор обоих гиперпараметров на максимизации предельного правдоподобия модели или, что эквивалентно, на максимизации апостериорной вероятности гиперпараметров λ и γ при плоском априорном распределении для этих гиперпараметров. Это означает максимизацию способности модели прогнозировать на один шаг вперед вне выборки. Действительно, логарифмически-маргинальное правдоподобие (или байесовское доказательство) можно интерпретировать как сумму предсказательных оценок на один шаг вперед, поскольку оно эквивалентно правилу подсчета очков в форме

Как следствие, калибровка γ и λ для максимизации (27) соответствует нахождению γ и λ, максимизирующих способность модели к прогнозированию на один шаг вперед вне выборки. Эта стратегия оценки гиперпараметров путем максимизации предельного правдоподобия является эмпирическим байесовским методом, который имеет четкую частотную интерпретацию. В дальнейшем, и в частности в алгоритме оценки, подробно описанном в следующем разделе 2.5, я буду рассматривать γ и λ как случайные величины и выполнять полный апостериорный вывод по гиперпараметрам, но аналогично максимизация апостериорной вероятности гиперпараметров будет соответствовать максимизации прогнозируемости модели на один шаг вперед вне выборки. Выполнив те же шаги, что и в работе Джанноне и др. (2015), мы можем переписать уравнение (27) как

2.5 Оценка

где p(γ) и p(λ) являются априорными для гиперпараметров сжатия 18, тогда как p(θ) является априорным значением глубоких параметров из теории. Следовательно, изучение структурных параметров происходит неявно путем проецирования оценок VAR на ограничения, подразумеваемые моделью из теории. Точнее, оценки глубоких параметров минимизируют взвешенное расхождение между неограниченными оценками TVP-VAR и функцией ограничения (18). Этот подход можно рассматривать как байесовскую версию Смита-младшего (1993), и он был впервые предложен Дель Негро и др. (2004). В частности, TVP-VAR используется для обобщения статистических свойств как наблюдаемых данных, так и данных, смоделированных теорией, а оценка глубоких параметров из теории получается путем сопоставления как можно более близких параметров TVP-VAR из наблюдаемых данных и из смоделированных данных.19 Для выборки из p(λ, θ, γ|Y ) я рассматриваю двухблочный алгоритм случайного блуждания метрополии. Это в основном сэмплер Гиббса, где в первом блоке я вывожу гиперпараметры γ и λ условно на θ, а во втором блоке я вывожу θ условно на сжимающихся гиперпараметрах γ и λ. Шаг 2, вместо этого, состоит только из Монте-Карло, вывожу из апостериора (Σu, Φ) условно на λ, γ и θ, что является нормальным-обратным-распределением Уишарта в (21), которое равно:

[4.] Этот момент будет более подробно рассмотрен в разделе 2.4.

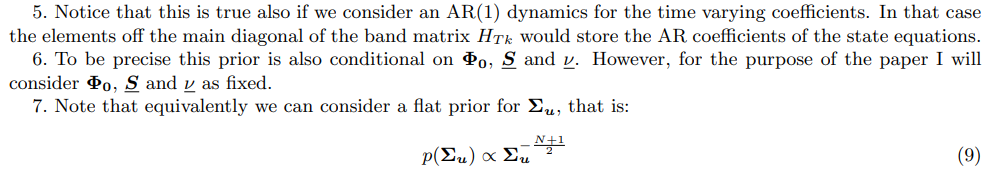
[8.] В приложении A.1.3 я сообщаю подробности о константе интегрирования.

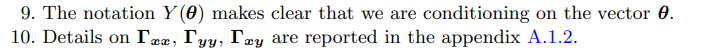
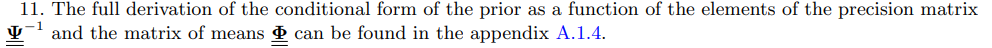
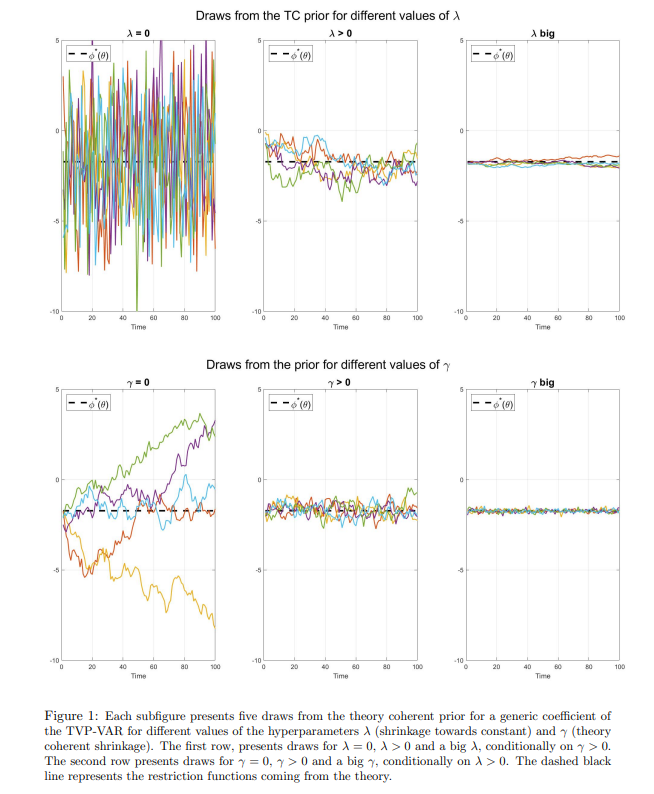
[12.] Обратите внимание, что отрисовка коэффициентов, изменяющихся во времени, была начата вблизи функций ограничения только в целях визуализации.

[13.] Коэффициенты будут иметь вырожденное распределение с точечной массой на функции ограничения.

[14.] В приложении A.1.1 я показываю, что благодаря структуре Кронекера априорной вероятности (6) изменение коэффициентов во времени можно моделировать с помощью фиктивных наблюдений.

[15.] Действительно, как и в прецизионном сэмплере Чана и др. (2009), мы можем извлечь все скрытые состояния из t = 1, . . . , T за один шаг, и благодаря структуре Кронекера апостериора мы можем сделать это для всех N уравнений TVP-VAR совместно. В более общем плане, структура Кронекера (19) в сочетании с прецизионным сэмплером Чана и др. (2009) может быть использована для оценки TVP-VAR среднего и большого масштаба.

[16.] Когда и γ = 0, и λ = 0, модель остается полностью неограниченной, с априорной ковариацией дисперсии коэффициентов, равной бесконечности. Очевидно, в этом случае имеется больше параметров, чем вы можете реально оценить с плоским априорным значением, что означает, что условная апостериорная вероятность Φ не может быть вычислена из-за необратимости X′X (это можно увидеть из уравнения (21)).

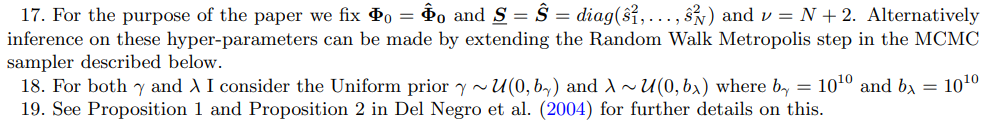
[20.] Формулы для предельного правдоподобия и условного апостериорного распределения Φ и Σu можно найти в приложении A.1.6.