Теория когерентного сокращения изменяющихся во времени параметров в VAR: анализ в ZLB

Таблица ссылок

Аннотация и введение

Теория когерентного TVP-VAR

Прогнозирование с помощью TC-TVP-VAR

Анализ ответа в ZLB с TC-TVP-VAR

Заключение и ссылки

Приложение

4 Анализ ответа в ZLB с TC-TVP-VAR

TVP-VAR широко используются в прикладных исследованиях не только для прогнозирования, но и для вывода изменений в реакции экономики на макроэкономические шоки. В этом разделе я показываю, что предлагаемое сокращение априорных значений может быть также полезно для улучшения вывода на импульсных функциях отклика, оцененных с помощью TVP-VAR. Недавние исследования в области эмпирической макроэкономики использовали

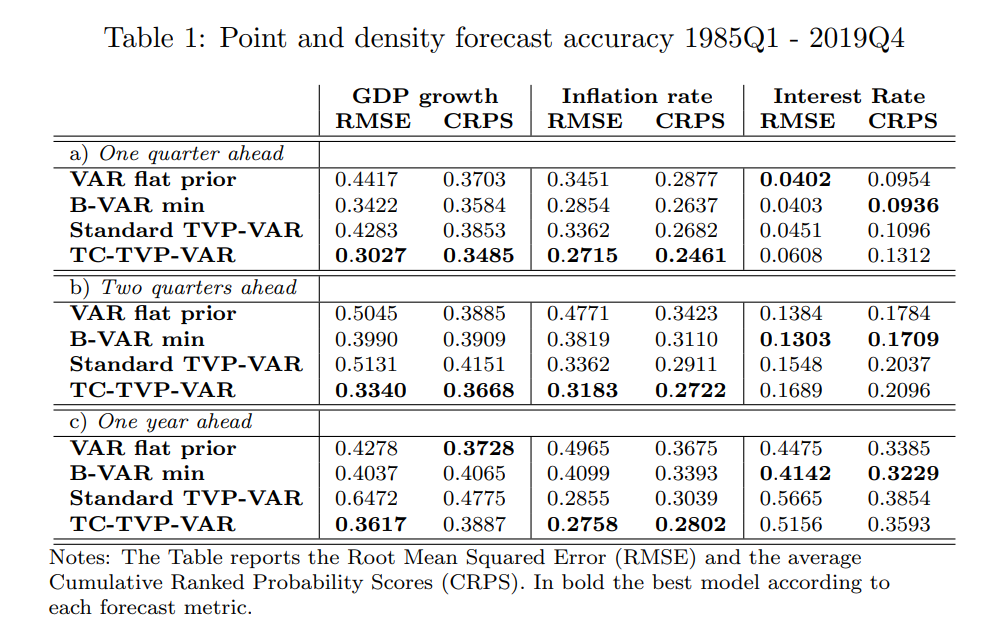
TVP-VAR для оценки того, повлияло ли на производительность экономики США связывающее ограничение ZLB (Debortoli et al. 2019; Benati et al. 2023). Фактически, согласно стандартной новой кейнсианской модели, ожидается, что экономика будет демонстрировать разные реакции, когда действует ограничение ZLB. Например, модель предсказывает отчетливую реакцию выпуска и инфляции после шоков как спроса, так и предложения, когда традиционная стабилизирующая реакция денежно-кредитной политики на совокупные шоки ограничена вследствие того, что ставка по федеральным фондам достигает ZLB. Рисунок 3 подчеркивает это, показывая реакции на чистый шок спроса (шок предпочтений) в версии модели Smets et al. (2007), рассмотренной в Del Negro et al. (2015).[24] Как и ожидалось, когда денежно-кредитная политика ограничивается ставкой политики, достигающей нулевой нижней границы, реакция как производства, так и инфляции на шок предпочтений усиливается при воздействии, а эффект шока спадает гораздо медленнее с течением времени.

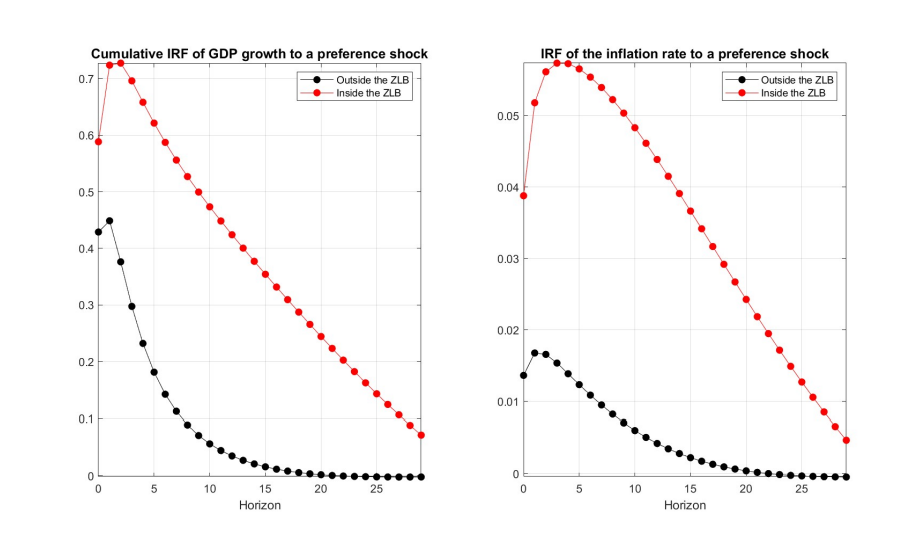
Несмотря на резкую разницу в распространении шоков в экономике внутри и за пределами периода нулевой нижней границы, предусмотренного стандартной моделью NK, эмпирические данные, исследующие этот вопрос, неоднозначны, и многие исследования не находят существенных доказательств, подтверждающих иную реакцию экономики США в период нулевой нижней границы. Например, Debortoli et al. (2019) поддерживают гипотезу нерелевантности, т. е. гипотезу о том, что на эффективность экономики не повлияло связывающее ограничение ZLB, придерживаясь мнения о том, что нетрадиционная денежно-кредитная политика оказалась эффективной для обхода ограничения нулевой нижней границы (ZLB). Benati et al. (2023) недавно показали, что, учитывая короткую продолжительность периода нулевой нижней границы, вывод, основанный на стандартной TVP-VAR, где изменяющиеся во времени параметры рассматриваются как медленно движущиеся стохастические процессы, не позволяет уловить изменяющуюся взаимосвязь между макроэкономическими переменными в течение периода ZLB, предсказанного новой кейнсианской моделью. В дальнейшем, основываясь на исследовании симуляции, я также обнаруживаю, что стандартная TVP-VAR с трудом обнаруживает изменение в ответах экономики в период ZLB, сгенерированное моделью NK. Я показываю, что TC-TVP-VAR в принципе может быть использована для решения этой выведенной проблемы и, следовательно, для восстановления отчетливого ответа экономики в период нулевой нижней границы.

4.1 Среднемасштабная модель NK с учетом ZLB и прямого направления

Новая кейнсианская модель — это версия модели Сметса и др. (2007), рассмотренной в работе Дель Негро и др. (2015). Модель включает в себя липкость цен и заработной платы, издержки корректировки инвестиций, формирование привычек в потреблении и 7 шоков, а именно шоки денежно-кредитной политики, технологические шоки, шоки ценовой надбавки, шоки надбавки к заработной плате, шоки предпочтений, шоки фискальной политики и шоки предельной эффективности капитала. В модели правило денежно-кредитной политики учитывает период ZLB и направление вперед.[25] Более конкретно, при учете нулевой нижней границы и направления вперед решение модели подразумевает представление пространства состояний, которое демонстрирует изменяющиеся во времени коэффициенты. Метод решения следует подходу, разработанному Кальярини и др. (2013) для линейных стохастических моделей рациональных ожиданий в условиях конечной последовательности ожидаемых структурных изменений. В частности, предполагается, что в заданный период t агенты ожидают, что номинальная процентная ставка будет на уровне ZLB для периодов H¯. То есть правило денежно-кредитной политики

4.2 Моделирование исследования

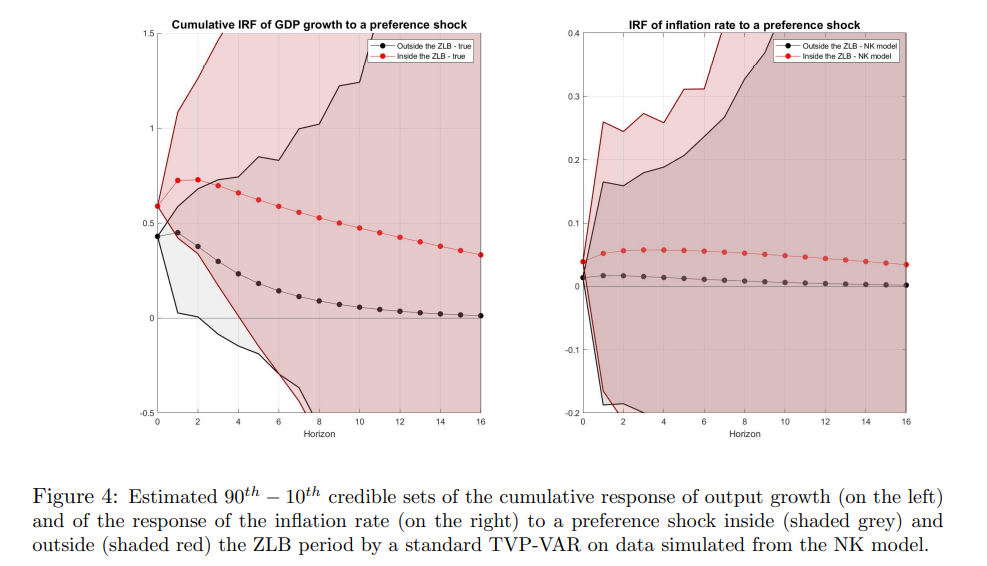
Как предполагалось выше и показано на рисунке 3, модель NK предсказывает отчетливую реакцию экономики на шок спроса внутри и вне периода ZLB. Обусловливая вектор глубоких параметров модели NK, я моделирую данные из представления пространства состояний (48) и (49). 28 В моделировании я рассматриваю искусственные выборки с T = 139, имитирующие квартальные наблюдения за период 1985Q1-2019Q3. Продолжительность периода ZLB составляет 28 кварталов, охватывая период 2009Q1-2015Q3. Я оцениваю стандартную модель TVP-VAR (Chan et al. 2009) на моделируемых данных, чтобы понять, способна ли модель восстановить изменение в реакции экономики в течение периода ZLB, сгенерированное моделью NK. 29 На рисунке 4 показаны предполагаемые реакции выпуска и инфляции на шок предпочтений, полученные с помощью стандартной TVP-VAR. На рисунке показаны реакции роста выпуска (кумулятивного) и уровня инфляции на шок предпочтения в одно стандартное отклонение в двух контрольных датах, одна вне периода ZLB, а другая внутри. Для того чтобы определить шоки в структурной TVP-VAR, я использую истинную матрицу воздействия модели NK, заданную как

4.3 Оценка TC-TVP-VAR на данных США

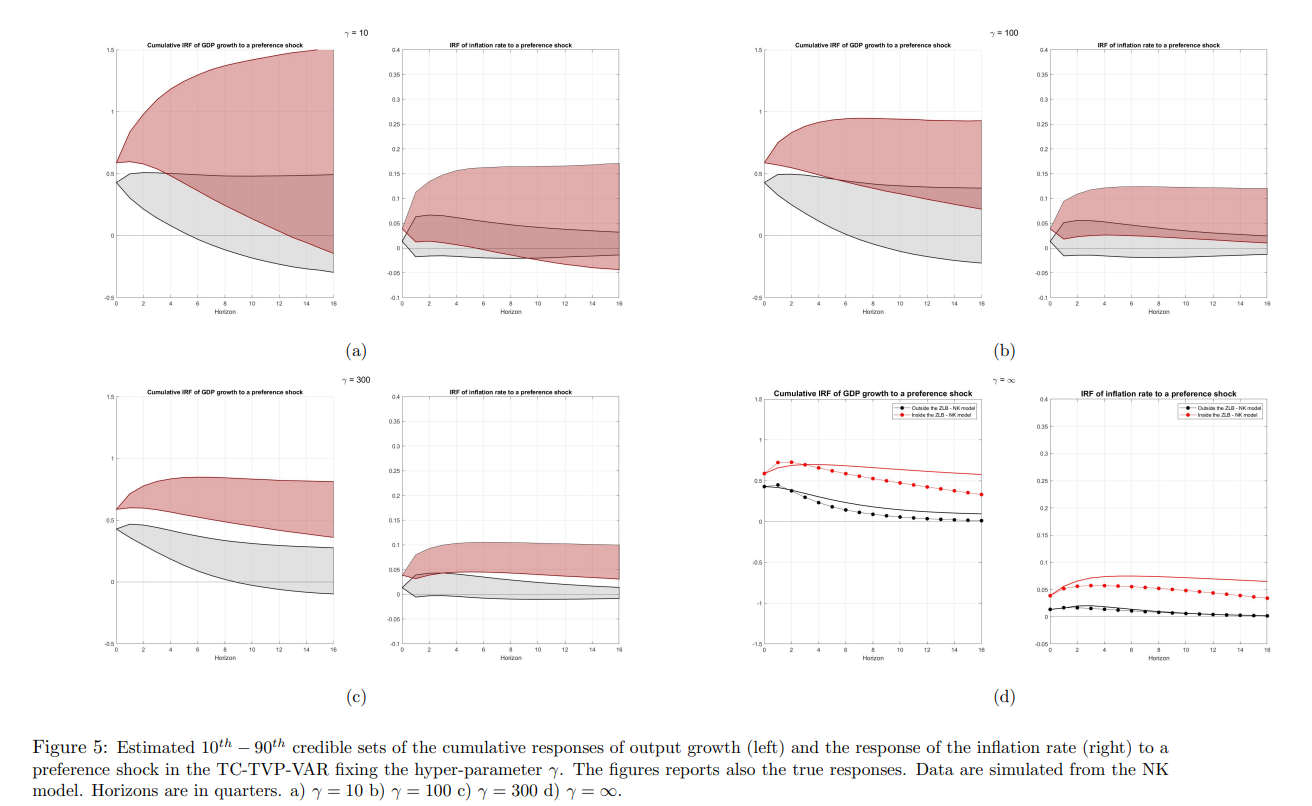
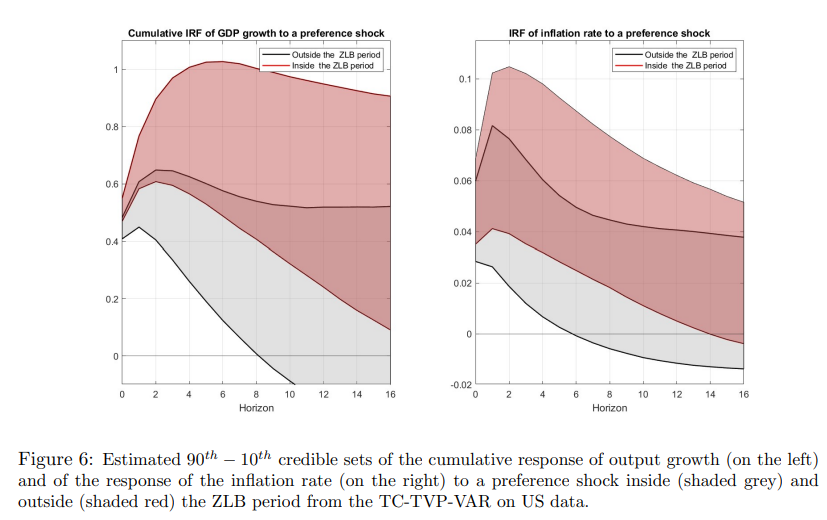
При анализе реальных данных разумно думать о модели NK просто как о приближенном (скорее всего, неверно заданном) жестко параметризованном представлении истинного процесса генерации данных. Другими словами, мы не ожидаем, что ограничения, подразумеваемые моделью NK, будут точно соблюдаться. Однако, будучи закодированными в априорной модели, эти ограничения могут оказаться полезными для получения более точных оценок коэффициентов, изменяющихся во времени, и нелинейных функций этих коэффициентов, таких как функции импульсного отклика. В частности, в нашем контексте сокращение может оказаться особенно полезным для обнаружения изменения реакции экономики в период ZLB, предсказанного моделью NK. Чтобы проанализировать, в какой степени данные поддерживают изменяющееся поведение в течение ZLB, мой подход заключается в использовании новой кейнсианской модели в качестве априорной для TC-TVP-VAR. Степень, в которой прогнозы из новой кейнсианской модели будут подкреплены данными, будет зависеть от оценочного апостериорного распределения γ, гиперпараметра, управляющего степенью сжатия параметров в сторону ограничения, подразумеваемого новой кейнсианской моделью. Если апостериорное распределение γ сосредоточено относительно далеко от нуля, коэффициенты TVP-VAR будут сжаты в сторону ограничений, подразумеваемых моделью NK, а оценочные отклики из TC-TVP-VAR будут напоминать прогнозы модели NK. Это произойдет на практике, если ограничения из модели NK найдут достаточную поддержку в данных. И наоборот, если ограничения из NK считаются неправдоподобными данными, апостериорное распределение γ будет сосредоточено вокруг нуля, и оценки изменяющихся во времени коэффициентов не будут отражать ограничения, исходящие из априорных. Оценочная модель представляет собой TC-TVP-VAR с 7 переменными для экономики США, включая рост производства, рост потребления, рост инвестиций, рост реальной заработной платы, отработанные часы, инфляцию и ставку Федерального резервного фонда, и она оценивается по выборке 1985Q1-2019Q32. Чтобы определить шоки в структурной TVP-VAR, я использую матрицу воздействия модели NK. Глубокие параметры модели NK рассматриваются как неизвестные и оцениваются вместе с другими параметрами модели, что подразумевает, что при воздействии существует неопределенность относительно эффекта шоков на переменные системы. На рисунке 6 показаны оценочные отклики от TC-TVP-VAR, где гиперпараметр γ оценивается вместе с другими параметрами модели. Апостериорное распределение γ оценивается как сконцентрированное далеко от нуля, что означает, что изменяющиеся во времени функции ограничения из модели NK находят достаточную поддержку в данных. Это, в свою очередь, отражается в оценках 10-90-х достоверных наборов, которые предоставляют некоторые доказательства, подтверждающие различные реакции экономики внутри и вне периода ZLB. Как и предсказывает модель NK, оценки предполагают, что когда денежно-кредитная политика ограничена номинальной ставкой, достигающей ZLB, шок предпочтений поглощается экономикой гораздо медленнее. После положительного шока спроса и рост выпуска, и уровень инфляции увеличиваются, причем влияние на рост выпуска оценивается точнее на более коротких горизонтах. Влияние на выпуск достигает пика почти через два квартала вне периода ZLB, в то время как примерно через пять кварталов внутри периода ZLB. Что касается инфляции, то эффект достигает пика через один квартал вне периода ZLB и через два квартала внутри периода ZLB. После пика влияние шока предпочтений как на выпуск, так и на инфляцию затухает гораздо медленнее внутри периода ZLB, как и предсказывает модель NK.

[24.] В этой модели период ZLB рассматривается так же, как у Дель Негро и др. (2015), а более подробная информация о модели будет приведена в следующем подразделе.

[25.] Лог-линеаризованные условия равновесия модели можно найти в приложении A.3. Модель обозначена как «SW» в работе Дель Негро и др. (2015) и предполагает постоянную цель инфляции.

[26.] Следуя за Del Negro et al. (2015), для измерения количества кварталов H¯, в течение которых ставка по федеральным фондам, как ожидается, останется на уровне ZLB, я использую информацию, основанную на ставках индексных свопов овернайт (OIS). В частности, я определяю период ZLB как кварталы, в которых ставка OIS ниже 0,35. Эта классификация приводит к тому же периоду ZLB, который рассматривался в Benati et al. (2023) и Debortoli et al. (2019), а именно 2009Q1-2015Q3 (28 кварталов). Следуя за Chen et al. (2012), я предполагаю, что количество кварталов, в течение которых ставка политики, как ожидается, останется фиксированной, не превышает четырех.

[27.] Подробности уравнений наблюдения приведены в приложении А.3 вместе со списком глубинных структурных параметров θ (приложение А.3.1).

[28.] Параметры калибруются в соответствии с апостериорным методом в Del Negro et al. (2015)

[29.] Стандартная модель TVP-VAR — это модель Чана и др. (2009). Для оценки модели я использую коды MATLAB, любезно предоставленные Джошуа Чаном на его личном сайте.

[30.] Как показано в приложении на рисунке 8, этот результат не обусловлен этой конкретной смоделированной выборкой искусственных наблюдений.

[31.] Также в этом случае в TC-TVP-VAR мы обуславливаем правильную схему идентификации для структурных шоков.

[32.] Подробная информация о переменных и их преобразовании доступна в приложении A.3.