
Теория когерентного сжатия изменяющихся во времени параметров в VAR: Приложение
5 сентября 2024 г.Андреа Ренцетти, факультет экономики, Alma Mater Studiorium Universit`a di Bologna, Piazza Scaravilli 2, 40126 Болонья, Италия.
Таблица ссылок
Аннотация и введение
Теория когерентного TVP-VAR
Прогнозирование с помощью TC-TVP-VAR
Анализ ответа в ZLB с TC-TVP-VAR
Заключение и ссылки
Приложение
Приложение
A.1 Теория когерентного TVP-VAR
A.1.1 Параметры, изменяющиеся во времени, по фиктивным наблюдениям
Начиная с:

мы можем записать TVP-VAR в статической компактной форме как:

Предположим, что мы хотим определить независимые стохастические процессы RW для всех коэффициентов в Φ как:

Это просто другой способ записи:

A.1.2 Моменты населения


A.1.3 Интегральная константа теории когерентного априорного распределения
Интегральная константа нормально-обратного априорного распределения Уишарта
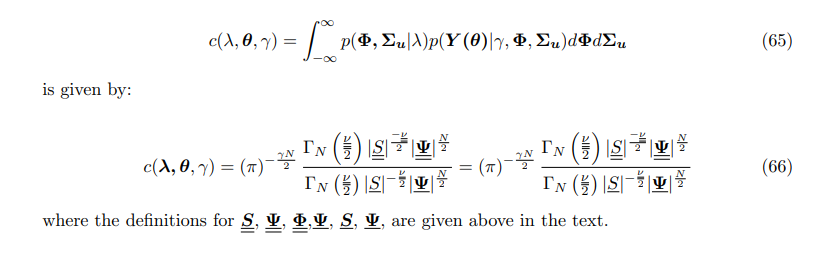
A.1.4 Условное распределение теории, согласованной с предшествующей

Учитывая первые три блока получаем

A.1.5 Предельная вероятность и компромисс между сложностью и соответствием
Предельная вероятность определяется по формуле:

Следуя тем же шагам, что и в (Giannone et al. 2015), это можно переписать следующим образом:

A.1.6 Формулы с различными λj для j = 1, . . . ,K
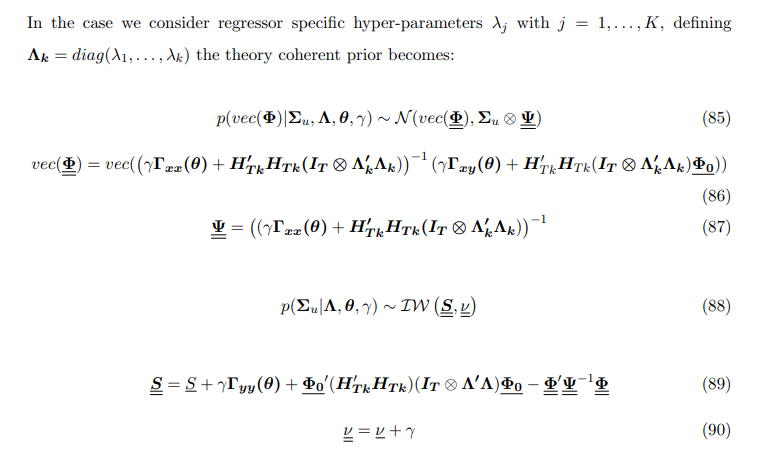

A.2 Маломасштабная новая кейнсианская модель для прогнозирования
А.2.1 Данные
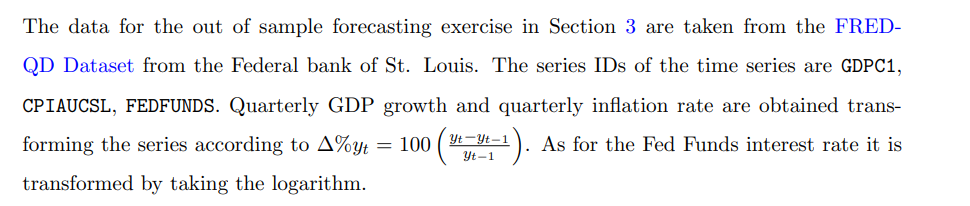
A.2.2 Конкурирующие модели в прогнозировании
Конкурирующие модели в упражнении по прогнозированию вне выборки в Разделе 3:
• VAR с постоянными параметрами и плоским априорным распределением.
• VAR с постоянными параметрами и нормальным обратным распределением Уишарта.
• Модель TVP-VAR
VAR с нормальным обратным априорным распределением Уишарта определяется по формуле:
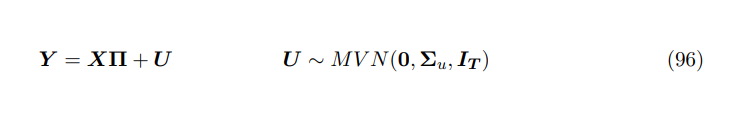

A.2.3 Предшествующие параметры DSGE
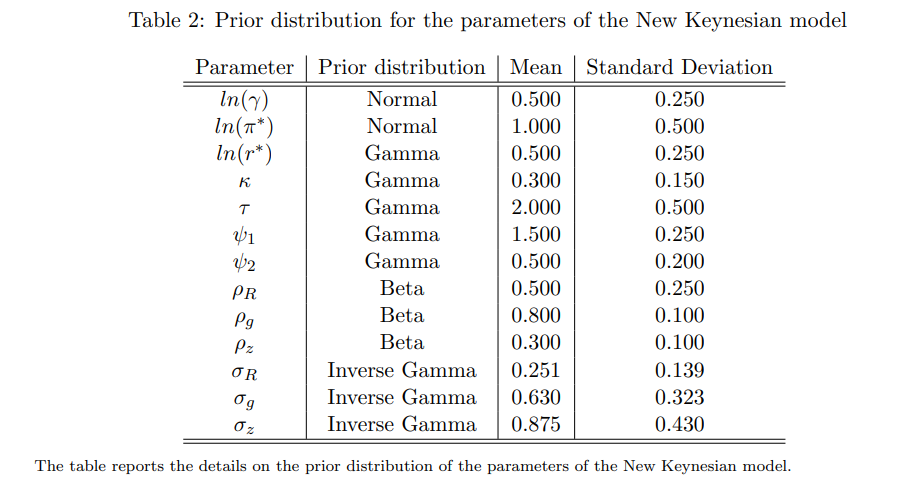
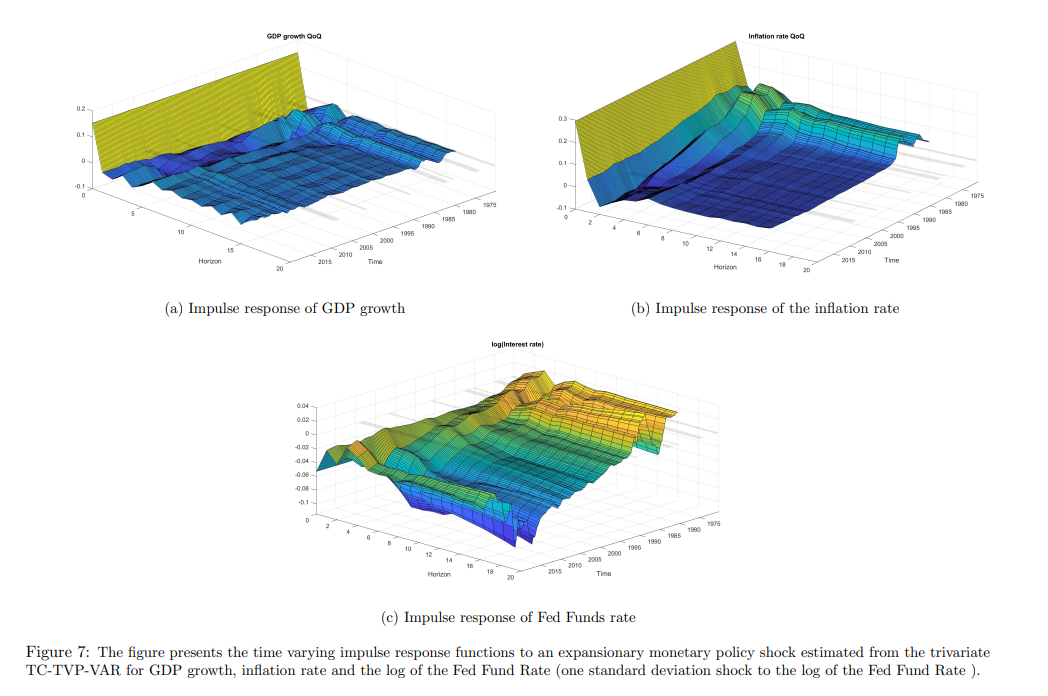
A.2.4 Апостериорная оценка параметров DSGE и IRF из TC-TVPVAR

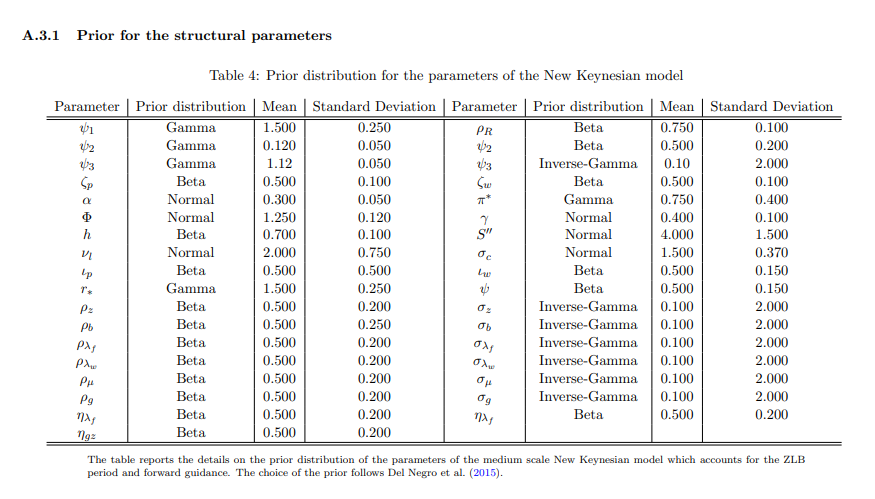
A.3 Среднемасштабная новая кейнсианская модель
Модель взята из Del Negro et al. (2015) и является версией популярной среднемасштабной новой кейнсианской модели в Smets et al. (2007). Набор логарифмически линеаризованных условий равновесия модели:
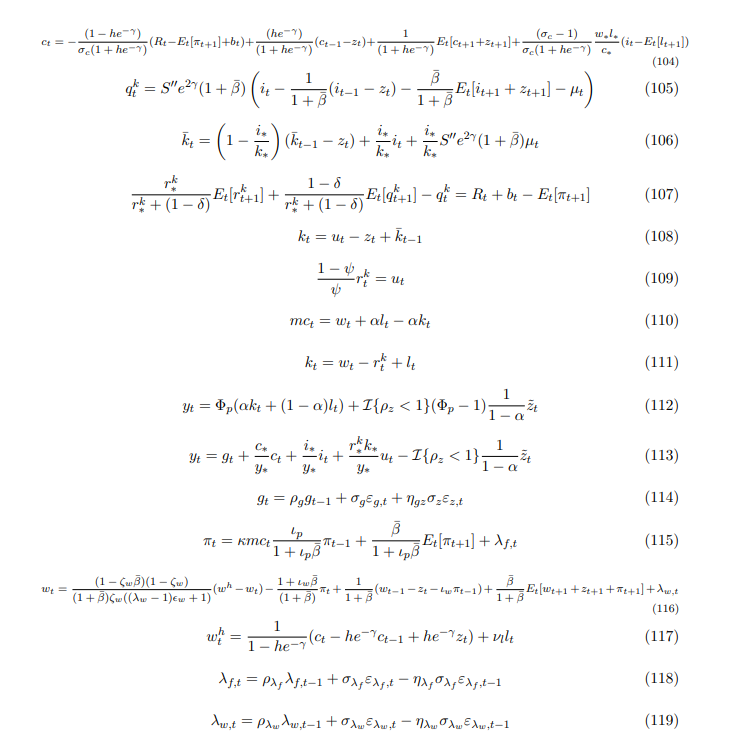

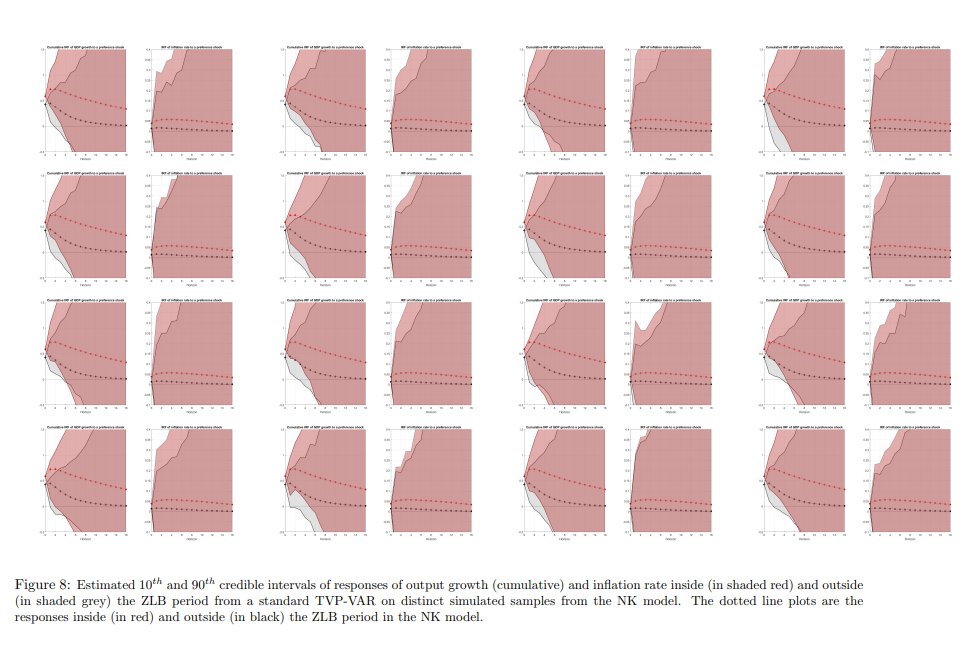
Эта статьядоступно на arxivпо лицензии CC 4.0.

Оригинал

