Теоремы развития.
30 октября 2023 г.Логическое исчисление Джорджа Буля входит в серию книг HackerNoon. Вы можете перейти к любой главе этой книги здесь. Теоремы развития.
Теоремы развития.
(1) Если x — любой выборный символ, то
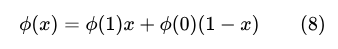
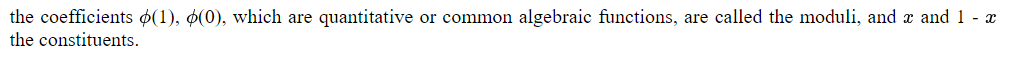
(2) Для функции двух выборных символов
n 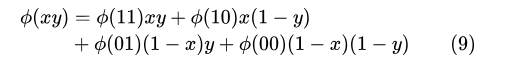
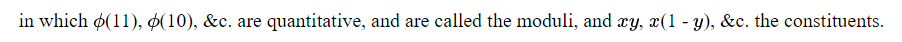
(3) Функции трех символов,
n 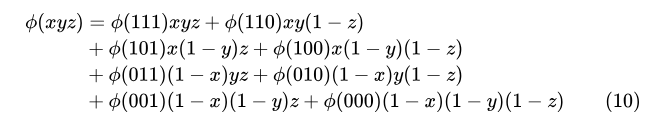 n
n 
Из этих примеров очевиден общий закон развития. И я хочу отметить, что этот закон является простым следствием основных законов, выраженных в (1), (2), (3).
n 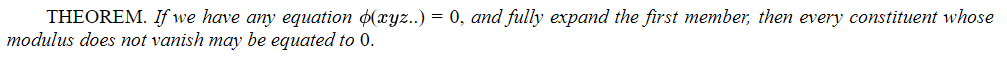
Это позволяет нам интерпретировать любое уравнение по общему правилу.
ПРАВИЛО. Приведите все члены к первой стороне, разложите ее по всем включенным в нее выборным символам и приравняйте 0 каждой составляющей, модуль которой не обращается в нуль.
n Для демонстрации этих и многих других результатов я должен обратиться к оригинальной работе. Необходимо отметить, что на стр. 66[4], z по ошибке заменен на w, и что ссылка на стр. 80[5] должно быть в предложении 2.
В качестве примера возьмем уравнение
n 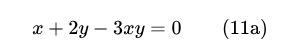
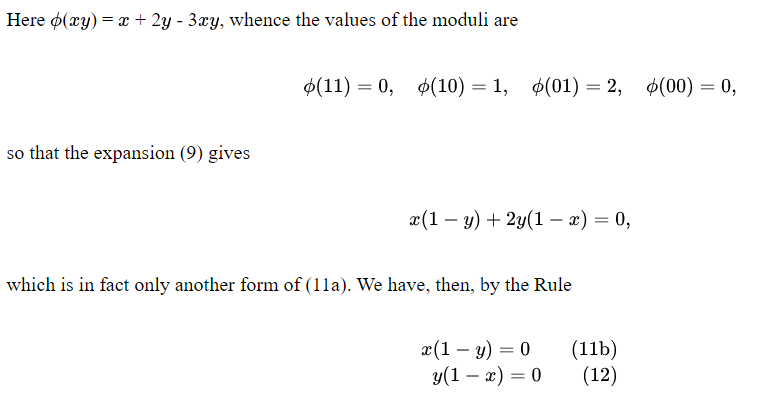
первое подразумевает, что не существует X, которые не были бы Y, второе - что не было Y, которые не были бы X; вместе они выражали полный смысл исходного уравнения.
n Однако мы часто можем рекомбинировать составляющие для упрощения. В данном случае, вычитая (12) из (11b), имеем
n 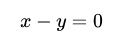
или
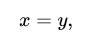
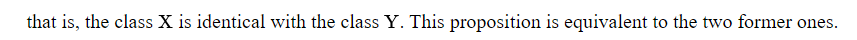
Таким образом, все уравнения имеют одинаковую значимость и при разложении дают одну и ту же серию составляющих уравнений, и все они поддаются интерпретации.
[4] Математический анализ логики
[5] Там же.
О книжной серии HackerNoon: мы предлагаем вам наиболее важные технические, научные и познавательные книги, являющиеся общественным достоянием.
Эта книга является общественным достоянием. Джордж Буль (2022). Логическое исчисление. Урбана, Иллинойс: Проект Гутенберг. Получено в октябре 2022 г. https://www.gutenberg.org/cache/epub/69512/pg69512-images. .html
Эта электронная книга предназначена для использования кем угодно и где угодно, бесплатно и практически без каких-либо ограничений. Вы можете скопировать ее, отдать или повторно использовать в соответствии с условиями лицензии Project Gutenberg, включенной в данную электронную книгу или на сайте www.gutenberg.org, расположен по адресу https://www.gutenberg.org/policy/license.html.
Оригинал

