
Методы, которые мы использовали для прогнозирования изменений свободной энергии связывания, вызванных мутациями
21 марта 2024 г.:::информация Этот документ доступен на arxiv под лицензией CC 4.0.
Авторы:
(1) Доктор Масуд Рана, факультет математики, Университет Кентукки;
(2) Дык Дуй Нгуен, факультет математики, Университет Кентукки и amp; ducnguyen@uky.edu.
:::
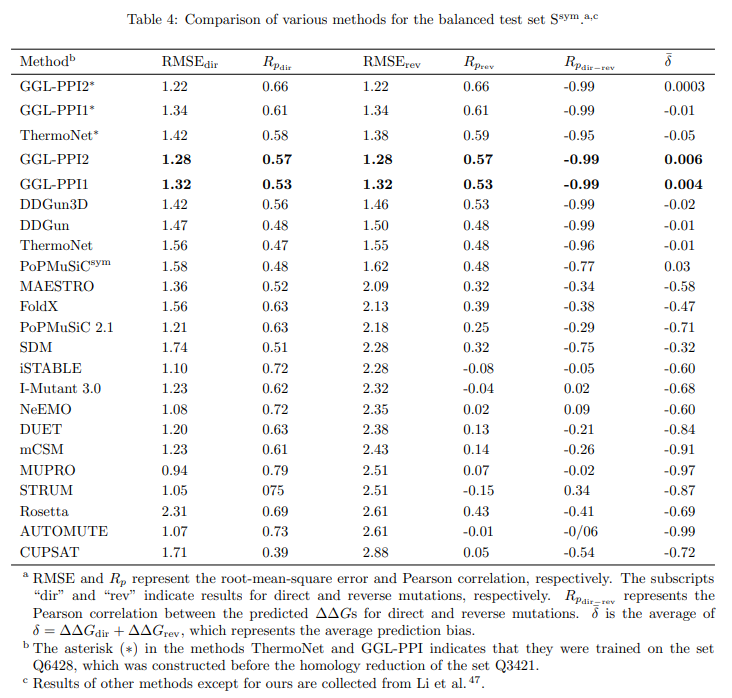
Таблица ссылок
3 метода
3.1 Теория графов и взаимодействия на уровне атомов в биомолекулах
Теория графов обеспечивает математическую основу, которая широко применяется при изучении биомолекул, таких как белки, ДНК и РНК. Для биомолекулы граф G(V, E) представляет собой набор узлов V и ребер E, которые могут представлять связность и отношения между различными атомами или остатками внутри молекулы.
Уточнением этого представления является раскраска графов — метод, который присваивает уникальные метки различным типам атомов внутри биомолекулы. Этот обогащенный цветной график кодирует разнообразные атомарные взаимодействия, открывая путь к коллективному и подробному описанию набора данных. В этом представлении атомы с назначенными метками организованы в подграфы, а цветные края между ними представляют взаимодействия, специфичные для атомов.
Преимущество использования подграфов заключается в их способности фокусироваться на конкретных областях или компонентах биомолекулы. Изолируя соответствующие подмножества атомов, подграфы позволяют нам идентифицировать локализованные закономерности, взаимодействия или кластеры, которые могут быть не очевидны в представлении глобального графа. Такой целенаправленный подход обеспечивает более детальное понимание структурных и функциональных свойств биомолекул.
Чтобы извлечь информацию о взаимодействии на уровне атомов, мы рассматриваем конкретные типы атомов на основе их имен в структуре PDB, таких как углерод альфа (CA), углерод бета (CB), углерод дельта-1 (CD1) и т. д. Эти имена атомов служат идентификаторы конкретных позиций в трехмерной структуре белка. Они помогают определить отдельные атомы, из которых состоят
аминокислоты, строительные блоки белков, и предоставляют важную информацию об их пространственной ориентации и химических свойствах. Мы рассматриваем в общей сложности 37 различных названий атомов, которые часто встречаются в белковых структурах в базе данных PDB. Эти типы атомов представлены множеством A.
Для упрощения обозначений мы предполагаем, что множество A отсортировано в буквенно-цифровом порядке,
A = {C, CA, CB, · · · , N, ND1, ND2, · · · , O, OD1, · · · , SD, SG},
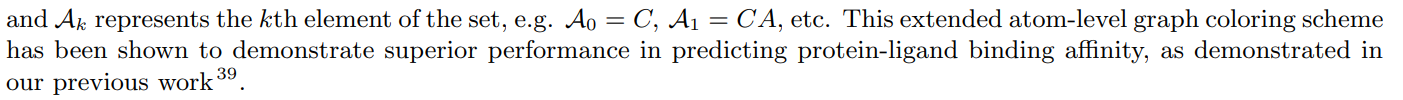

служит мерой совокупной силы взаимодействия между выбранными парами типов атомов, обеспечивая ценную информацию о молекулярной структуре и свойствах.
3.2 Представление ИЦП геометрическим подграфом
В контексте изучения белок-белковых взаимодействий (PPI) и прогнозирования влияния мутаций на эти взаимодействия важно сосредоточиться на соответствующих регионах, где происходят взаимодействия.
Хотя белок-белковые комплексы могут состоять из большого числа атомов, взаимодействия между белками в основном происходят в определенных областях, известных как интерфейсы. Чтобы сократить вычислительные затраты и сконцентрироваться на важной информации, принято рассматривать только атомы белка вблизи мест связывания.
Сайт связывания в этом контексте относится к участку, находящемуся на определенном расстоянии c от цепи, где произошла мутация. Определив таким образом сайт связывания, мы можем сузить наше внимание до конкретной области, где взаимодействие и последующие эффекты мутации наиболее выражены.
Кроме того, при анализе последствий мутаций крайне важно включать информацию о геометрических графах из сайтов мутаций и соседних с ними областей. Сайт мутации определяется как область на расстоянии c от мутированного остатка, что позволяет нам уловить структурные изменения, возникающие в результате мутации.
Чтобы построить сайт-специфическое многомасштабное представление взвешенного цветного геометрического подграфа (MWCGS) для PPI, рассматриваются белки как дикого типа, так и мутантного типа. Это приводит к четырем наборам характеристик для каждого PPI, соответствующим двум сайтам и двум типам задействованных белков. Каждый набор состоит из 37 × 37 = 1369 признаков MWCGS, представляющих взаимодействия между типами атомов, участвующих в PPI.
Эти особенности включают в себя разнообразные химические и биологические свойства, такие как наличие специфических межатомных взаимодействий с участием атомов кислорода и азота, гидрофобная природа определенных областей и способность атомов подвергаться поляризации, среди других соответствующих молекулярных характеристик.
Используя эти специфические для сайта функции MWCGS, мы можем получить ценную информацию о влиянии мутаций и лежащих в их основе молекулярных взаимодействиях, раскрывая важную информацию и характеристики, заложенные в систему PPI.
3.3 Изучение геометрических графиков для PPI
Точное предсказание изменений аффинности связывания, вызванных мутациями в белок-белковых комплексах, представляет собой серьезную проблему из-за сложной природы этих систем. Взаимодействия между белками очень сложны, а эффекты мутаций могут быть незаметными и зависеть от контекста.
Методы машинного обучения предлагают многообещающий подход к решению этой проблемы, используя возможности моделей на основе данных для выявления сложных закономерностей и взаимосвязей.
Алгоритмы машинного обучения могут помочь в прогнозировании изменений аффинности связывания, вызванных мутациями, путем обучения на наборе обучающих примеров, состоящих из белково-белковых комплексов с известными экспериментальными аффинностями связывания.
Эти алгоритмы могут анализировать признаки, извлеченные из комплексов, такие как информация геометрического графа, для выявления соответствующих закономерностей и ассоциаций между признаками и близостью привязки. Изучая эти закономерности, алгоритмы могут обобщать и делать прогнозы относительно невидимых белково-белковых комплексов.
Существует несколько алгоритмов машинного обучения, которые можно использовать в сочетании с функциями геометрического графа для прогнозирования изменений сродства связывания. Эти алгоритмы включают случайные леса [49], машины опорных векторов (SVM) [50], нейронные сети [51] и деревья повышения градиента (GBT) [52]. У каждого алгоритма есть свои сильные и слабые стороны, а их производительность может варьироваться в зависимости от конкретной задачи и набора данных.
Среди этих алгоритмов в последние годы значительную популярность приобрели деревья повышения градиента (GBT) [39]. GBT — это ансамблевый метод, который строит последовательность слабых учеников, обычно деревья решений, для исправления ошибок, допущенных предыдущими учениками.
Объединив этих слабых учеников, GBT может эффективно моделировать сложные отношения и повышать точность прогнозов. Одним из преимуществ GBT является его устойчивость к переоснащению, что особенно полезно при работе с умеренным количеством функций.
Кроме того, модели GBT могут обеспечить интерпретируемость, что позволяет нам получить представление о факторах, способствующих изменениям аффинности связывания.
Для реализации алгоритма GBT в этом исследовании использовался пакет scikit-learn (версия 0.24.1). Чтобы оптимизировать производительность модели GBT для ансамблевых методов, были точно настроены конкретные гиперпараметры.
Число оценок было установлено равным 40000, что указывает на количество слабых учащихся в ансамбле, а скорость обучения была установлена на 0,001, определяя вклад каждого слабого обучающегося в окончательный прогноз.
Учитывая большое количество функций, задействованных в задаче прогнозирования, эффективный процесс обучения был достигнут за счет ограничения максимального количества рассматриваемых функций квадратным корнем из длины дескриптора. Такой подход помог ускорить процесс обучения без ущерба для общей производительности модели GBT.
Чтобы обеспечить надежную оценку производительности, для каждого набора функций было выполнено пятьдесят прогонов с использованием различных случайных начальных чисел. Путем усреднения результатов, полученных в результате этих прогонов, был получен более надежный и репрезентативный показатель производительности.
Несмотря на сложность задачи прогнозирования и задействование множества функций, выбранные настройки параметров и несколько прогонов дали удовлетворительные результаты производительности.
Подход GBT был выбран из-за его способности эффективно справляться с переоснащением, демонстрировать хорошую производительность с наборами данных среднего размера и предоставлять интерпретируемые модели.
Эти характеристики делают GBT подходящим и надежным выбором для данного исследования, позволяя точно прогнозировать вызванные мутациями изменения аффинности связывания в белок-белковых комплексах с использованием предоставленных геометрических графических особенностей.
:::информация Этот документ доступен на Arxiv под лицензией CC 4.0.
:::
Оригинал

