Математика задачи переключателя лампочек: сколько лампочек останется включенными после N раундов?

27 апреля 2023 г.

Если вы заинтересованы в решении сложных математических задач и хотите улучшить свое логическое мышление и навыки программирования, вам следует прочитать эту статью о задаче "Переключатель лампочек".

Эта задача представляет собой классическую головоломку, для решения которой требуется немного математической интуиции и тщательного анализа. В статье дается четкое объяснение проблемы и рассматриваются шаги, необходимые для ее решения. Чтение этой статьи поможет вам лучше понять проблему и предоставит вам полезный инструмент для решения подобных проблем в будущем.

В этой статье описывается несколько решений и подходов, что делает ее весьма полезным ресурсом для всех, кто интересуется проблемой «переключателя лампочек».

Описание

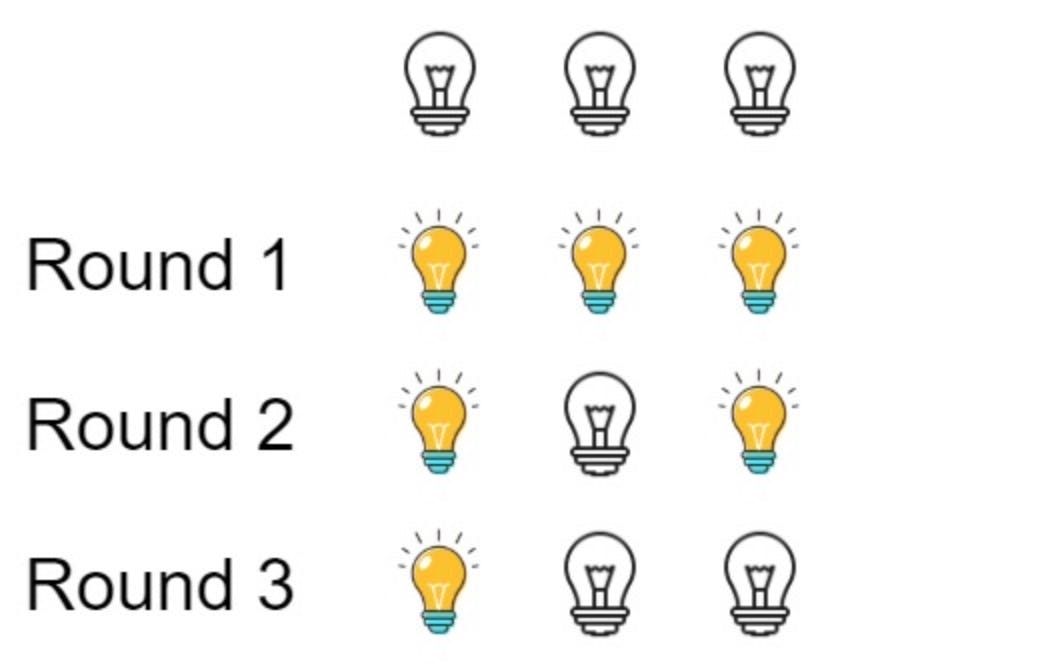
Есть n лампочек, которые изначально не горят. Сначала вы включаете все лампочки, а затем выключаете каждую вторую лампочку.

В третьем раунде вы включаете каждую третью лампочку (включается, если она выключена, или выключается, если она включена). В раунде ith вы переключаете каждую лампочку i. В n-м раунде вы включаете только последнюю лампочку.

Возвращает количество лампочек, которые горят после n раундов.

Первое решение

Решение этой проблемы заключается в том, чтобы найти закономерность в процессе переключения лампочек. После первого раунда горят все лампочки. После второго раунда все остальные лампочки выключаются. После третьего раунда включается каждая третья лампочка. Этот шаблон продолжается до n-го раунда, где переключается только n-я лампочка.

Замечено, что для любого данного раунда будут гореть лампочки с нечетным числом факторов. Например, число 6 имеет делители 1, 2, 3 и 6. В третьем раунде будут переключаться лампочки 1, 2, 3 и 6. Лампы 1 и 6 загорятся, так как у них нечетное количество множителей, а лампочки 2 и 3 погаснут, так как у них четное количество множителей.

Следовательно, чтобы решить задачу, нам нужно подсчитать количество целых чисел от 1 до n, имеющих нечетное количество множителей. Это можно сделать эффективно, используя свойство квадратного корня: каждое целое число, являющееся полным квадратом, имеет нечетное число множителей. Следовательно, количество лампочек, которые будут гореть после n раундов, равно количеству правильных квадратов, меньшему или равному n.

fun bulbSwitch(n: Int): Int {

количество переменных = 0

для (i в 1..n) {

если (i * i <= n) {

количество++

} иначе {

перерыв

количество возвратов

Второе решение

fun bulbSwitcher(n: Int): Int {

вернуть kotlin.math.sqrt(n.toDouble()).toInt()

В этом решении используется тот факт, что количество переключений лампочки равно количеству факторов, которые она имеет. Например, лампочка 6 переключается в раундах 1, 2, 3 и 6, поэтому у нее 4 множителя. Лампочка будет гореть только в конце, если у нее нечетное количество множителей, потому что двойное включение лампочки нейтрализует эффект ее однократного включения.

Единственные числа, которые имеют нечетное число делителей, являются полными квадратами. Таким образом, количество лампочек, которые будут гореть в конце, равно количеству правильных квадратов, меньшему или равному n. Мы можем вычислить это, взяв квадратный корень из n и округлив до ближайшего целого числа.

В первом решении используется логический массив для представления состояния каждой лампочки, где true означает, что лампочка включена, а false означает, что лампочка выключена. Затем он повторяет раунды и переключает статус лампочек в соответствии с заданными правилами. Наконец, он подсчитывает количество включенных лампочек и возвращает результат.

Во втором решении также используется логический массив для представления состояния каждой лампочки, но вместо повторения раундов и переключения состояния лампочки вычисляется количество факторов для каждой лампочки. Если количество факторов нечетное, лампочка горит; в противном случае он выключен. Затем он подсчитывает количество включенных лампочек и возвращает результат.

Оба решения используют одну и ту же структуру данных и возвращают один и тот же результат, но второе решение использует другой подход к определению состояния каждой лампочки путем подсчета ее факторов, в то время как первое решение переключает состояние каждой лампочки на основе заданных правил.< /p>

В целом, статья представляет собой хороший пример того, как подходить к такой проблеме, как выключатель лампы, и как найти эффективные решения, используя различные подходы. Это также показывает важность анализа проблемы и понимания лежащих в ее основе математических концепций для поиска наиболее оптимального решения.

---

Оригинал