История метагеометрии

24 октября 2022 г.

Эссе Бертрана Рассела об основах геометрии входит в серию книжных публикаций HackerNoon. Таблицу ссылок для этой книги можно найти по адресу здесь. Основы геометрии, глава 1: краткая история метагеометрии

ОСНОВЫ ГЕОМЕТРИИ. ГЛАВА I.

КРАТКАЯ ИСТОРИЯ МЕТАГЕОМЕТРИИ.

Когда нападению подвергается давно устоявшаяся система, обычно бывает так, что нападение начинается только в одном месте, где особенно очевидна слабость устоявшейся доктрины. Но критика, однажды приглашенная, склонна простираться гораздо дальше, чем поначалу желали бы самые смелые.

«Сначала разжижение разрезают, а что потом, Но ловко Фихте разрезает самого бога?» Так было и с геометрией. Разжижение евклидовой ортодоксии есть аксиома параллелей, и с отказа принять эту аксиому без доказательства началась метагеометрия. Первая попытка Лежандра в этом направлении была вдохновлена ​​надеждой вывести эту аксиому из других — надеждой, которая, как мы теперь знаем, была обречена на неизбежный провал. Лежандр определяет параллели как прямые, лежащие в одной плоскости, так что если их пересечет третья линия, то сумма внутренних и противоположных углов будет равна двум прямым углам. Он без труда доказывает, что такие прямые не пересекаются, но не может доказать, что непараллельные прямые на плоскости должны пересекаться. Точно так же он может доказать, что сумма углов треугольника не может превышать двух прямых углов, и что если в каком-либо треугольнике сумма равна двум прямым углам, то все треугольники имеют одинаковую сумму; но он не может доказать существование этого единственного треугольника.

Таким образом, попытка Лежандра провалилась; но простая неудача ничего не могла доказать. Более смелый метод, предложенный Гауссом, был реализован Лобачевским и Бойяи. Если аксиома параллелей логически выводима из других, то мы, отрицая ее и сохраняя остальные, придем к противоречиям. Эти три математика, соответственно, подошли к проблеме косвенно: они отрицали аксиому параллелей и тем не менее получили логически непротиворечивую геометрию. Они пришли к выводу, что эта аксиома логически независима от других и существенна для евклидовой системы. Их работы, вдохновленные этим мотивом, можно назвать первым периодом в развитии метагеометрии.

Второй период, начатый Риманом, имел гораздо более глубокое значение: он был в значительной степени философским по своим целям и конструктивным по своим методам. Он был направлен не менее чем на логический анализ всех основных аксиом геометрии и рассматривал пространство как частный случай более общей концепции многообразия. Опираясь на методы аналитической метрической геометрии, она установила две неевклидовы системы: первую систему Лобачевского, вторую, в которой также отрицалась аксиома прямой линии в форме Евклида, новую разновидность, аналог называется сферическим. Ведущим понятием в этот период является мера кривизны, термин, изобретенный Гауссом, но примененный им только к поверхностям. Гаусс показал, что свободная подвижность на поверхностях возможна только тогда, когда мера кривизны постоянна; Риман и Гельмгольц распространили это утверждение на n измерений и сделали его фундаментальным свойством пространства.

В третьем периоде, который начинается с Кэли, философский мотив, который двигал первыми пионерами, менее очевиден и заменен более техническим и математическим духом. Этот период отличается главным образом от второго с математической точки зрения своим методом, который является проективным, а не метрическим. Ведущим математическим понятием здесь является Абсолют (Grundgebild), фигура, по отношению к которой все метрические свойства становятся проективными. Работа Кэли, которая была очень краткой и привлекла мало внимания, была усовершенствована и развита Ф. Кляйном и благодаря ему нашла всеобщее признание. Клейн добавил к уже известным двум видам неевклидовой геометрии третий, который он назвал эллиптической; этот третий вид очень похож на сферическую геометрию Гельмгольца, но отличается тем важным отличием, что в нем две прямые линии встречаются только в одной точке.

Отличительной чертой пространств, представляемых обоими, является то, что, подобно поверхности сферы, они конечны, но не ограничены. Сведение метрических свойств к проективным, как будет показано ниже, имеет только техническое значение; в то же время проективная геометрия может иметь дело непосредственно с теми чисто описательными или качественными свойствами пространства, которые являются общими как для Евклида, так и для метагеометрии. Следовательно, третий период имеет большое философское значение, тогда как его метод математически более красив и цельен, чем метод второго; он способен рассматривать все виды пространства одновременно, так что каждое символическое суждение, в соответствии со значением, придаваемым символам, является суждением в той геометрии, которую мы выбираем. Это имеет то преимущество, что доказывает, что дальнейшие исследования не могут привести к противоречиям в неевклидовых системах, если они в то же время не обнаруживают противоречий в Евклиде. Таким образом, эти системы логически столь же верны, как и система самого Евклида.

После этого краткого описания характеристик трех периодов я перейду к более подробному описанию. Моя цель будет заключаться в том, чтобы, насколько это возможно, избегать всей технической математики и выделять только те фундаментальные моменты в развитии математики, которые кажутся важными с точки зрения логики или философии.

Первый период.

Создатель всей системы, Гаусс, по-видимому, в отношении строго неевклидовой геометрии ни в одной из своих до сих пор опубликованных работ не дал ничего, кроме результатов; его доказательства остаются нам неизвестными. Тем не менее он был первым, кто исследовал последствия отрицания аксиомы параллелей и в своих письмах сообщал об этих следствиях некоторым своим друзьям, среди которых был Вольфганг Бойяи. Первое упоминание об этом предмете в его письмах происходит, когда ему было всего 18 лет; четыре года спустя, в 1799 г., в письме к В. Бойяи он сформулировал важную теорему о том, что в гиперболической геометрии существует максимум площади треугольника. Из более поздних работ следует, что он разработал систему почти, если не совсем, столь же полную, как у Лобачевского и Бойяи.

Важно, однако, помнить, что работа Гаусса по кривизне, которая была опубликована, заложила основу всего метода второго периода и была предпринята, согласно Риману и Гельмгольцу, с целью (неопубликованной ) исследование основ геометрии. Его работа в этом направлении, благодаря ее методу, будет лучше рассмотрена во второй период, но интересно отметить, что он стоял, как и многие пионеры, во главе двух тенденций, которые впоследствии разошлись.

Лобачевский, профессор Казанского университета, впервые опубликовал свои результаты на их родном русском языке в трудах этого ученого органа за 1829–1830 годы. Из-за этой двойной неизвестности языка и места они привлекали мало внимания, пока он не перевел их на французский и немецкий языки: даже тогда они, похоже, не получили должного внимания, пока в 1868 году Бельтрами не обнаружил статью в Крелле. , и сделал его темой блестящей интерпретации.

В предисловии к своей небольшой немецкой книге Лобачевский сетует на слабый интерес, проявленный к его трудам его соотечественниками, и на невнимание математиков после неудачной попытки Лежандра к трудностям в теории параллелей. Основная часть работы начинается с формулировки нескольких важных утверждений, которые справедливы как для предлагаемой системы, так и для Евклида: некоторые из них в любом случае не зависят от аксиомы параллелей, тогда как другие передаются таковыми путем замены вместо слово «параллельный», фраза «не пересекающиеся, как бы далеко они ни производились». Затем следует определение, намеренно составленное так, чтобы противоречить евклидовскому: по отношению к данной прямой линии все остальные в той же плоскости могут быть разделены на два класса: те, которые пересекают данную прямую, и те, которые ее не пересекают; линия, являющаяся границей между двумя классами, называется параллельной данной прямой. Отсюда следует, что из любой внешней точки можно провести две параллели, по одной в каждом направлении. Из этой отправной точки с помощью евклидова синтетического метода выводится ряд предложений; наиболее важным из них является то, что в треугольнике сумма углов всегда меньше или всегда равна двум прямым углам, тогда как в последнем случае вся система становится ортодоксальной. Доказывается также некоторая аналогия со сферической геометрией, смысл и объем которой будут раскрыты позже, состоящая примерно в замене круговых функций гиперболическими.

Очень похожа система Иоганна Бойяи, настолько похожа, что делает независимость двух произведений, хотя и хорошо подтвержденным фактом, почти невероятной. Иоганн Бойяи впервые опубликовал свои результаты в 1832 году в приложении к работе своего отца Вольфганга под названием; «Приложение, scientiam spatii absolute veram exhibens: a veritate aut falsitate Axiomatis XI. Euclidei (a priori haud unquam Choosenda) Independentem; adjecta ad casum falsitatis, quadratura circuli геометрическая». Гаусс, закадычным другом которого он стал в колледже и остался на всю жизнь, был, как мы видели, вдохновителем Вольфганга Бойяи и имел обыкновение говорить, что последний был единственным человеком, который ценил его философские рассуждения об аксиомах геометрии; тем не менее, Вольфганг, похоже, оставил своему сыну Иоганну детальную разработку гиперболической системы.

Работы обоих Бойяи очень редки, и их метод и результаты известны мне только по изображениям Фришауфа и Хальстеда. Как по методу, так и по результатам система очень похожа на систему Лобачевского, так что ни то, ни другое не должно нас здесь останавливать. Краткого внимания требуют лишь исходные постулаты, более четкие, чем у Лобачевского. Введение Фришауфа, имеющее философский и ньютоновский характер, начинается с утверждения, что геометрия имеет дело с абсолютным (пустым) пространством, полученным путем абстрагирования от находящихся в нем тел, что две фигуры называются конгруэнтными, если они различаются только положением, и что аксиома конгруэнтности необходима при любом определении пространственных величин. Конгруэнтность должна была относиться к геометрическим телам, не обладающим ни одним из свойств обычных тел, кроме непроницаемости (Эрдманн, Аксиома геометрии, стр. 26). Прямая линия определяется двумя своими точками, а плоскость определяется тремя. Эти посылки, за небольшим исключением относительно прямой линии, мы впоследствии найдем существенными для всякой геометрии. Я обратил на них внимание, так как часто предполагается, что неевклидцы отрицают аксиому конгруэнтности, чего здесь и в других местах никогда не бывает. Акцент, сделанный Бойяи на этой аксиоме, вероятно, связан с влиянием Гаусса, чья работа о кривизне поверхностей заложила основу для использования конгруэнтности Гельмгольцем.

Важно помнить, что на протяжении только что рассмотренного нами периода цель гиперболической геометрии носит косвенный характер: не истинность последней, а логическая независимость аксиомы параллелей от остальных является руководящим мотивом работы. . Если, отрицая аксиому параллелей при сохранении остальных, мы можем получить систему, свободную от логических противоречий, то отсюда следует, что аксиома параллелей не может имплицитно содержаться в других. Если это так, то попытки отказаться от аксиомы, как у Лежандра, не могут быть успешными; Евклид должен стоять или падать с подозреваемой аксиомой. Конечно, оставалось возможным, что при дальнейшем развитии в этих системах могли обнаружиться скрытые противоречия. Эта возможность, однако, была устранена более прямой и конструктивной работой второго периода, на которую мы должны теперь обратить внимание.

Второй период.

Работа Лобачевского и Бойяи почти четверть века оставалась бесплодной — действительно, исследования Римана и Гельмгольца, когда они появились, по-видимому, были вдохновлены не этими людьми, а скорее Гауссом и Гербартом. Соответственно, мы находим очень большую разницу как в целях, так и в методах между первым периодом и вторым. Первый, начав с критики одного пункта системы Евклида, сохранил свой синтетический метод, отбросив при этом одну из его аксиом. Последняя, ​​напротив, руководствуясь скорее философским, чем математическим духом, стремилась классифицировать понятие пространства как вид более общего понятия: оно трактовало пространство алгебраически, а свойства, которые оно придавало пространству, выражалось в терминах , не интуиция, а алгебра.

Целью Римана и Гельмгольца было показать путем демонстрации логически возможных альтернатив эмпирический характер принятых аксиом. С этой целью они представили пространство как частный случай многообразия и показали, что в расширенном многообразии математически возможны различные отношения величин (Massverhältnisse). Их философия, которая кажется мне не всегда безупречной, будет обсуждаться в главе II; здесь, хотя важно помнить о философских мотивах Римана и Гельмгольца, мы ограничим наше внимание математической стороной их работы. При этом, хотя мы, я боюсь, несколько исказим систему их мыслей, мы обеспечим более тесное единство предмета и более компактное изложение чисто математического развития. Но есть, на мой взгляд, еще одна причина отделить их философию от их математики. В то время как их философская цель состояла в том, чтобы доказать, что все аксиомы геометрии эмпиричны и что иное содержание нашего опыта могло бы изменить их все, непреднамеренным результатом их математической работы было, если я не ошибаюсь, предоставление материала для априорное доказательство некоторых аксиом.

Эти аксиомы, хотя они и считали их ненужными, всегда вводились в их математических работах, прежде чем закладывались основы неевклидовых систем. В главе III я утверждаю, что это удержание было логически неизбежным, а не просто следствием, как они предполагали, желания соответствовать опыту. Если я прав в этом, то между Риманом и Гельмгольцем-философами и Риманом и Гельмгольцем-математиками существует расхождение. Это расхождение делает более желательным проследить развитие математики отдельно от сопутствующей философии.

Эпохальная работа Римана «Ueber die Hypothesen, welche der Geometrie zu Grande liegen» была написана и прочитана узкому кругу в 1854 году; однако из-за некоторых изменений, которые он хотел внести в нее, она оставалась неопубликованной до 1867 г., когда она была опубликована его душеприказчиками. Две фундаментальные концепции, на изобретении которых основывается историческое значение этой диссертации, — это концепция многообразия и концепция меры кривизны многообразия. Первая концепция служит главным образом философским целям и предназначена главным образом для того, чтобы показать пространство как пример более общей концепции. Об этом аспекте многообразия мне придется много говорить в главе II; его математический аспект, который нас здесь интересует, менее сложен и менее плодотворен для споров. Последняя концепция также служит двойной цели, но ее математическое использование более заметно. Мы последовательно рассмотрим эти две концепции.

(1) Концепция многообразия. Общая цель диссертации Римана состоит в том, чтобы представить аксиомы как последовательные шаги в классификации видового пространства. Аксиомы геометрии, подобно знакам схоластического определения, выступают как последовательные определения классовых понятий, заканчивающиеся евклидовым пространством. Таким образом, с аналитической точки зрения мы имеем настолько логичную и точную формулировку, насколько это возможно, — формулировку, в которой, благодаря ее классификационному характеру, мы кажемся уверенными в том, что в ней нет ничего лишнего или избыточного, и мы получаем аксиомы в явном виде. наиболее желательной форме, а именно как прилагательные концепции пространства. В то же время жаль, что Риман, в соответствии с метрическим пристрастием своего времени, рассматривал пространство прежде всего как величину или совокупность величин, в которой главная проблема состоит в том, чтобы приписать величины различным элементам или точкам. без учета качественного характера приписываемых величин. Таким образом, возникает значительная неясность относительно всей природы величины. Этот взгляд на геометрию лежит в основе определения многообразия как общего понятия, частным случаем которого является пространство. Это определение, которое не очень ясно, можно представить следующим образом.

Представления о величине, по Риману, возможны только там, где мы имеем общее понятие, способное к различным определениям (Bestimmungsweisen). Различные определения такого понятия вместе образуют многообразие, непрерывное или дискретное в зависимости от того, непрерывно или дискретно переход от одного определения к другому. Отдельные биты множества, или кванты, можно сравнивать путем подсчета, когда они дискретны, и путем измерения, когда они непрерывны. «Измерение состоит в наложении сравниваемых величин. Если этого нет, то величины могут сравниваться только тогда, когда одна является частью другой, и тогда можно решить только больше или меньше, а не сколько» (с. 256).

Таким образом, мы приходим к общему понятию многообразия нескольких измерений, из которых пространство и цвета упоминаются как частные случаи. Отсутствию этой концепции Риман приписывает «неясность», которая в отношении аксиом «длилась от Евклида до Лежандра» (стр. 254). И с алгебраической точки зрения Риману, безусловно, удалось показать гораздо яснее, чем любой из его предшественников, аксиомы, отличающие пространственную величину от других величин, с которыми знакома математика. Но из-за предположения, с самого начала, что пространство можно рассматривать как количество, он был вынужден сформулировать проблему так: какой величины является пространство? а не: чем должно быть пространство, чтобы мы вообще могли рассматривать его как величину? Он также не осознает — а в его время мало кто осознавал, — что возможна сложная геометрия, которая вообще не имеет дело с пространством как с величиной. Таким образом, его определение пространства как вида многообразия, хотя для аналитических целей оно наиболее удовлетворительно определяет природу пространственных величин, оставляет неясным истинное основание этой природы, лежащее в природе пространства как системы отношений. и предшествует возможности вообще рассматривать его как систему величин.

Но продолжим математическое развитие идей Римана. Мы видели, что он объявлял измерение состоящим в суперпозиции сравниваемых величин. Но для того, чтобы это могло быть возможным средством определения величин, продолжает он, эти величины должны быть независимы от своего положения в многообразии (стр. 259). Это может происходить, говорит он, несколькими способами, в качестве простейшего из которых он предполагает, что длины линий не зависят от их положения. Было бы приятно узнать, какие другие пути возможны: я, со своей стороны, не могу представить никакой другой гипотезы, при которой величина не зависела бы от места. Однако если оставить это в стороне, проблема, благодаря тому, что измерение состоит в наложении, становится тождественной с определением самого общего многообразия, в котором величины не зависят от места. Это подводит нас к другой фундаментальной концепции Римана, которая кажется мне еще более плодотворной, чем концепция многообразия.

(2) Мера кривизны. Эта концепция принадлежит Гауссу, но применялась им только к поверхностям; новшеством в диссертации Римана было ее распространение на многообразие n измерений. Это расширение, однако, выражено довольно кратко и неясно, и еще более затемняется попытками Гельмгольца популяризовать изложение. Термин «кривизна» также вводит в заблуждение, так что даже среди математиков эта фраза стала источником большего непонимания, чем любая другая фраза в пангеометрии. Часто забывают, несмотря на явное утверждение Гельмгольца, что «мера кривизны» n-мерного многообразия есть чисто аналитическое выражение, имеющее лишь символическое родство с обычной кривизной. Применительно к трехмерному пространству вывод о четырехмерном «плоском» пространстве полностью вводит в заблуждение; Поэтому вместо этого я обычно буду использовать термин пространственная постоянная. Тем не менее, поскольку эта концепция исторически выросла из концепции кривизны, я дам очень краткое изложение исторического развития теорий кривизны

Точно так же, как понятие длины было первоначально получено из прямой линии и распространено на другие кривые путем разделения их на бесконечно малые прямые линии, так и понятие кривизны было получено из окружности и распространено на другие кривые путем разделения их на бесконечно малые дуги окружности. . Первоначально кривизну можно рассматривать как меру отклонения кривой от прямой линии; в круге, который везде одинаков, эта величина, очевидно, постоянна и измеряется обратной величиной радиуса. Но во всех других кривых величина кривизны варьируется от точки к точке, так что ее нельзя измерить без бесконечно малых величин. Сразу напрашивается мера кривизны круга, наиболее точно совпадающая с кривой в рассматриваемой точке. Поскольку окружность определяется тремя точками, эта окружность будет проходить через три последовательные точки кривой. Таким образом, мы определили кривизну любой кривой, плоской или извилистой; ибо, поскольку любые три точки лежат в плоскости, такую ​​окружность всегда можно описать.

Если мы теперь перейдем к поверхности, то, по аналогии, нам нужна мера ее отклонения от плоскости. Кривизна, определенная выше, стала неопределенной, так как через любую точку поверхности можно провести бесконечное число дуг, которые, вообще говоря, не будут иметь одинаковой кривизны. Итак, проведем все геодезические, соединяющие рассматриваемую точку с соседними точками поверхности во всех направлениях. Так как эти дуги образуют единое бесконечное многообразие, то среди них будут, если они не все имеют одинаковую кривизну, одна дуга максимальной и одна минимальной кривизны. Произведение этих максимальной и минимальной кривизны называется мерой кривизны поверхности в рассматриваемой точке.

Для иллюстрации на нескольких простых примерах: на сфере кривизна всех таких линий равна обратной величине радиуса сферы, следовательно, мерой кривизны везде является квадрат обратной величины радиуса сферы. На всякой поверхности, например на конусе или цилиндре, на которой можно провести прямые линии, они не имеют кривизны, так что мера кривизны везде равна нулю, в частности, на плоскости. Однако в целом мера кривизны поверхности варьируется от точки к точке. Гаусс, изобретатель этой концепции, доказал, что для того, чтобы две поверхности могли развертываться друг на друге, т.е. может быть таким, чтобы одну можно было согнуть в форму другой без растяжения или разрыва — необходимо, чтобы две поверхности имели одинаковую степень кривизны в соответствующих точках. Когда это так, каждая фигура, возможная на одном, вообще возможна на другом, и обе они имеют практически одинаковую геометрию. Отсюда следует, что необходимым условием свободного перемещения фигур на любой поверхности является постоянство меры кривизны. Это условие было доказано Миндингом как достаточным, так и необходимым.

До сих пор все шло гладко — мы имели дело с чисто геометрическими идеями чисто геометрическим образом, — но мы еще не нашли никакого смысла меры кривизны, в котором ее можно было бы распространить на пространство, все же меньше до n-мерного многообразия. Для этой цели мы должны изучить метод Гаусса, который позволяет нам определить меру кривизны поверхности в любой точке как неотъемлемое свойство, совершенно независимое от какой-либо ссылки на третье измерение.

Метод определения меры кривизны изнутри, вкратце, заключается в следующем: если любая точка на поверхности определяется двумя координатами u, v, то малые дуги поверхности задаются формулой

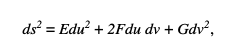
где E, F, G суть, вообще говоря, функции от u, v. Только по этой формуле, без привязки к какому-либо пространству вне поверхности, мы можем определить меру кривизны в точке u, v как функция E, F, G и их дифференциалов по u и v. Таким образом, мы можем рассматривать меру кривизны поверхности как неотъемлемое свойство, и приведенное выше геометрическое определение, которое включало ссылку на третье измерение, может быть упавший. Но здесь необходима осторожность. Он появится в гл. III. (§ 176), что логически невозможно установить точную систему координат, в которой координаты представляют собой пространственные величины, без аксиомы Свободной Подвижности, и эта аксиома, как мы только что видели, выполняется на поверхностях только тогда, когда мера кривизна постоянна. Следовательно, наше определение меры кривизны будет действительно свободным от ссылки на третье измерение только тогда, когда мы будем иметь дело с поверхностью постоянной меры кривизны — точкой, которую Риман полностью упускает из виду.

Это предостережение, однако, применимо только в пространстве, и если мы примем систему координат, как предполагается в концепции многообразия, мы можем вообще пренебречь этим предостережением, помня при этом, что возможность системы координат в пространстве включает в себя аксиомы, которые будут исследованы позже. . Таким образом, мы можем видеть, как можно найти смысл, безотносительно к какому-либо более высокому измерению, для постоянной меры кривизны трехмерного пространства или для любой меры кривизны n-мерного многообразия вообще. 22. Такой смысл придает диссертация Римана, к которой мы можем теперь вернуться после этого длинного отступления. Мы можем определить непрерывное многообразие как любой континуум элементов, такой, что один элемент определяется n непрерывно переменными величинами. Это определение на самом деле не включает пространство, поскольку координаты в пространстве определяют не точку, а ее отношение к началу координат, которое само по себе произвольно. Однако оно включает в себя аналитическую концепцию пространства, с которой имеет дело Риман, и поэтому на данный момент может быть оставлено без изменений. Затем Риман предполагает, что разница — или расстояние, как это можно условно назвать — между любыми двумя элементами сравнима по величине с разницей между любыми другими двумя. Далее он предполагает, что заслуга Гельмгольца в том, что он доказал, что разность ds между двумя последовательными элементами может быть выражена как квадратный корень из квадратичной функции разностей координат: т.е.

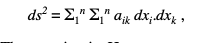
где коэффициенты aik являются, вообще говоря, функциями координат x1 x2 ... xn. Вопрос в том, как из этой формулы получить определение меры кривизны? Заметно, во-первых, что, как на поверхности мы нашли бесконечное число радиусов кривизны в точке, так и в многообразии трех или более измерений мы должны найти бесконечное число мер кривизны в точке. точки, по одной на каждое двумерное многообразие, проходящее через точку и содержащееся в высшем многообразии. Поэтому сначала нам нужно определить такие двумерные многообразия. Они должны состоять, как мы видели на поверхности, из одной бесконечной серии геодезических, проходящих через точку. Теперь геодезическая полностью определяется одной точкой и ее направлением в этой точке или одной точкой и следующей последовательной точкой. Следовательно, геодезическая через рассматриваемую точку определяется отношениями приращений координат, dx1 dx2 ... dxn. Предположим, у нас есть две такие геодезические, в которых i′-е приращение равно d′xi и d″xi соответственно. Тогда все геодезические, заданные

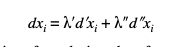
образуют бесконечный ряд, так как они содержат один параметр, а именно λ′: λ″. Таким образом, такой ряд геодезических должен образовывать двумерное многообразие с мерой кривизны в обычном гауссовском смысле. Эта мера кривизны может быть определена из приведенной выше формулы для элементарной дуги с помощью упомянутой выше общей формулы Гаусса. Таким образом, мы получаем бесконечное число мер кривизны в точке, но из n.(n – 1) 2 из них можно вывести остальные (Riemann, Gesammelte Werke, стр. 262). Когда все меры кривизны в точке постоянны и равны всем мерам кривизны в любой другой точке, мы получаем то, что Риман называет многообразием постоянной кривизны. В таком многообразии возможна свободная подвижность, и позиции по существу не отличаются друг от друга. Если a - мера кривизны, формула для дуги в этом случае принимает вид

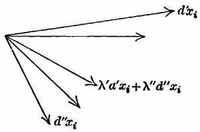
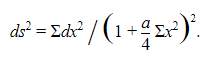
Только в этом случае, как я указал выше, термин «мера кривизны» может быть правильно применен к пространству без ссылки на более высокое измерение, поскольку свободная подвижность логически необходима для существования количественной или метрической геометрии.

23. Математический результат диссертации Римана можно резюмировать следующим образом. Если предположить, что к пространству можно применить величину, т. . Однако в силу своеобразия пространственного измерения количественное определение пространства требует, чтобы величины не зависели от места, а поскольку это не так, то наше измерение неизбежно будет неточным. Если мы теперь примем в качестве количественного отношения расстояния между двумя элементами квадратный корень из квадратичной функции координат — формула, впоследствии доказанная Гельмгольцем и Ли, — то из этого следует, что, поскольку величины не зависят от места, пространство должен в пределах наблюдения иметь постоянную меру кривизны или, другими словами, должен быть однородным во всех своих частях. В бесконечно малом, говорит Риман (стр. 267), наблюдение не могло обнаружить отклонение от постоянства со стороны меры кривизны; но он не пытается показать, как геометрия может оставаться возможной при таких обстоятельствах, и единственная построенная им геометрия полностью основана на свободной мобильности. Я постараюсь доказать в главе III, что любая метрическая геометрия, пытающаяся обойтись без этой аксиомы, была бы логически невозможна. Сейчас я только укажу, что Риман, несмотря на свое желание доказать, что можно обойтись без всех аксиом, тем не менее в своей математической работе сохранил три основные аксиомы, а именно Свободную Подвижность, конечное целое число измерений , и аксиому, что две точки имеют уникальное отношение, а именно расстояние. Они, как мы увидим далее, сохраняются в реальной математической работе всеми метрическими метагеометрами, даже если они верят, подобно Риману и Гельмгольцу, что никакие аксиомы не являются философски необходимыми.

24. Гельмгольц, исторически ближайший последователь Римана, руководствовался аналогичной эмпирической философией и независимо пришел к очень похожему методу формулирования аксиом. Хотя Гельмгольц ничего не публиковал по этому вопросу до самой смерти Римана, он тогда только что увидел диссертацию Римана (которая была опубликована посмертно) и разработал свои результаты, насколько они были тогда завершены, при полной независимости как от Римана, так и от Лобачевский. Гельмгольц, безусловно, является наиболее читаемым из всех писателей по метагеометрии, и его труды, почти единственные, представляют для философов современную математическую точку зрения на этот предмет. Но в этой области его значение гораздо больше как философа, чем как математика; почти единственным его оригинальным математическим результатом в отношении геометрии является доказательство формулы Римана для бесконечно малой дуги, и даже это доказательство было далеко не жестким, пока Ли не преобразовал его своим методом непрерывных групп. Поэтому в этой главе нас должны занять только две его работы, а именно две статьи в Wissenschaftliche Abhandlungen, Vol. II., озаглавленный соответственно «Ueber die thatsächlichen Grundlagen der Geometrie», 1866 г. (стр. 610 и далее), и «Ueber die Thatsachen, die der Geometrie zum Grunde liegen», 1868 г. (стр. 618 и далее).

25. В первом из них, в основном философском, Гельмгольц намекает на свою тогда еще незаконченную математическую работу, но в основном ограничивается изложением результатов. Он объявляет, что докажет квадратичную формулу Римана для бесконечно малой дуги; но для этого, говорит он, мы должны начать с конгруэнтности, так как без нее невозможно пространственное измерение. Тем не менее, он утверждает, что Конгруэнтность доказана опытом. Как мы могли бы без помощи измерений обнаруживать отклонения от Конгруэнтности, это вопрос, который он оставляет без обсуждения. Затем он формулирует четыре аксиомы, которые он считает существенными для геометрии, следующим образом:

(1) Что касается непрерывности и размеров. В пространстве n измерений точка однозначно определяется измерением n непрерывные переменные (координаты).

(2) Что касается существования подвижных твердых тел. Между 2n координатами любой пары точек твердого тела существует уравнение, которое то же самое для всех конгруэнтных пар точек. Рассматривая достаточное количество пар точек, мы получаем больше уравнений, чем неизвестных величин: это дает нам метод определения формы этих уравнений, чтобы сделать возможным их выполнение.

(3) Что касается свободной мобильности. Каждая точка может свободно и непрерывно переходить из одного положения в другое. Из (2) и (3) следует, что если две системы A и B можно привести в соответствие в каком-то одном положении, то это возможно и в любом другом положении .

(4) Относительно независимости вращения твердых тел (Монодромия). Если (n – 1) точек тела остаются фиксированными, так что каждая другая точка может описывать только определенную кривую, то эта кривая замкнута.

Эти аксиомы, говорит Гельмгольц, достаточны, чтобы вместе с аксиомой трех измерений дать евклидову и неевклидову системы как единственные альтернативы. То, что они достаточны с математической точки зрения, нельзя отрицать, но в некоторых отношениях кажется, что они заходят слишком далеко. Во-первых, нет необходимости применять аксиому конгруэнтности к действительным твердым телам — об этом предмете я подробно рассказал в главе II. Опять же, Свободная Подвижность, в отличие от Конгруэнтности, вряд ли нуждается в специальной формулировке: какой барьер может создать пустое пространство для движения точки? Аксиома связана с однородностью пространства, что то же самое, что и аксиома конгруэнтности. Монодромия также подвергалась резкой критике; не только очевидно, что оно могло быть включено в Congruence, но даже с чисто аналитической точки зрения Софус Ли доказал, что оно излишне. Таким образом, правильно сформулированная аксиома конгруэнтности включает в себя третью и четвертую аксиомы Гельмгольца и часть его второй аксиомы. Все четыре, или, вернее, те из них, которые относятся к геометрии, являются следствиями, как мы увидим далее, одного фундаментального принципа относительности положения.

26. Вторая статья, в основном математическая, содержит обещанное доказательство формулы дуги, которая является наиболее важным вкладом Гельмгольца в геометрию. Риман принял эту формулу как простейшую из множества альтернатив: Гельмгольц доказал, что она является необходимым следствием его аксиом. Настоящая статья начинается с краткого повторения первой, включая утверждение аксиом, к которым в конце статьи добавляются еще две: (5) что пространство имеет три измерения и (6) что пространство бесконечный. В тексте, как и в первой статье, предполагается, что мера кривизны не может быть отрицательной и, следовательно, бесконечное пространство должно быть евклидовым. Эта ошибка в обеих статьях исправлена ​​в примечаниях, добавленных после появления статьи Бельтрами об отрицательной кривизне. Это образец слегка непрофессионального характера математической работы Гельмгольца по этому предмету, который вызывает у Клейна следующие замечания: «Гельмгольц по профессии не математик, а физик и физиолог... Из этого нематематического качества Гельмгольца, естественно следует, что он не относится к математической части своей работы с тщательностью, которую можно было бы требовать от математика по профессии (фон Фах)». Он сам говорит нам, что именно физиологическое изучение зрения привело его к вопросу об аксиомах, и именно как физик он заставляет свои аксиомы относиться к действительным твердым телам. Соответственно, мы находим ошибки в его математике, такие как аксиома монодромии и предположение, что мера кривизны должна быть положительной. Тем не менее, доказательство формулы дуги Римана чрезвычайно убедительно и в целом подтверждено более тщательными исследованиями Ли.

27. Другие работы Гельмгольца по геометрии почти полностью философские и будут подробно обсуждаться в главе II. А пока мы можем перейти к единственному другому важному писателю второго периода, Бельтрами. Поскольку его работа чисто математическая и содержит мало спорных моментов, она, несмотря на ее большое значение, не должна нас долго задерживать.

«Saggio di Interpretazione della Geometria non-Euclidea», которое в основном ограничивается двумя измерениями, интерпретирует результаты Лобачевского характерным методом второго периода. Он показывает, развивая работу Гаусса и Миндинга, что все утверждения плоской геометрии, сформулированные Лобачевским, верны в обычном евклидовом пространстве на поверхностях постоянной отрицательной кривизны. Странно, как указывает Клейн, что эта интерпретация, известная Риману и, возможно, даже Гауссу, так долго оставалась без явного заявления. Это тем более странно, что "Géométrie Imaginaire" Лобачевского появилась в Crelle, Vol. XVII. а статья Миндинга, из которой сразу следует толкование, появилась в Crelle, Vol. XIX. Разум показал, что геометрию поверхностей постоянной отрицательной кривизны, в частности, что касается геодезических треугольников, можно вывести из геометрии сферы, придав радиусу чисто мнимое значение ia. Этот результат, как мы видели, также был получен Лобачевским для его «Геометрии», и все же потребовалось тридцать лет, чтобы связь была доведена до всеобщего сведения.

28. В Saggio Бельтрами прямые линии, конечно же, заменены геодезическими; его координаты получаются через поточечное соответствие вспомогательной плоскости, в которой прямые соответствуют геодезическим на поверхности. Таким образом, геодезические имеют линейные уравнения и всегда однозначно определяются двумя точками. Однако расстояния на поверхности не равны расстояниям на плоскости; таким образом, хотя поверхность бесконечна, соответствующая часть плоскости содержится в пределах некоторого конечного круга. Расстояние между двумя точками на поверхности есть определенная функция координат, а не обычная функция элементарной геометрии. Эти отношения плоскости и поверхности важны в связи с теорией расстояния Кэли, которую нам предстоит рассмотреть далее. Если бы мы определили расстояние на плоскости как функцию координат, которая дает соответствующее расстояние на поверхности, мы получили бы то, что Кляйн называет «плоскостью с гиперболической системой измерения (Massbestimmung)». в котором верна теория расстояния Кэли. Однако очевидно, что при установлении системы координат предполагалось обычное понятие расстояния, так что мы не получаем на самом деле альтернативных геометрий на одной и той же плоскости. Значение этих замечаний проявится более полно, когда мы перейдем к рассмотрению Кэли и Кляйна.

29. Ценность Saggio Бельтрами в его собственных глазах заключается в понятном евклидовом смысле, который он придает планиметрии Лобачевского: соответствующей системе объемной геометрии, поскольку она не имеет значения для евклидовой пространстве, почти не упоминается в этой работе. Однако во второй статье, написанной почти одновременно с первой, он переходит к рассмотрению общей теории n-мерных многообразий постоянной отрицательной кривизны. На эту статью большое влияние оказала диссертация Римана; она начинается с формулы для линейного элемента и доказывает из нее, во-первых, что для таких пространств выполняется конгруэнция, а во-вторых, что они имеют, согласно определению Римана, постоянную отрицательную меру кривизны. (Полезно заметить, что как в этом, так и в предыдущем очерке большое внимание уделяется необходимости аксиомы конгруэнтности.)

Эта работа представляет меньший философский интерес, чем предыдущая, поскольку она лишь повторяет в общей форме результаты, полученные Саджио для двух измерений, — результаты, которые тонут при распространении на n измерения, до уровня простых математических построений. Тем не менее статья важна как как восстановление отрицательной кривизны, которую проглядел Гельмгольц, так и как аналитическая обработка результатов Лобачевского — обработка, которая вместе с Saggio, наконец, вернула им известность, которую они заслуживали.

Третий период.

30. Третий период радикально отличается как по своим методам и целям, так и по основополагающим философским идеям от периода, который он заменил. В то время как во втором периоде все было основано на измерении с его аппаратом Конгруэнтности, Свободной Подвижности, Твердых Тел и т. д., все это полностью исчезает в третьем периоде, который, впадая в противоположную крайность, считает количество совершенно неуместным. категории в геометрии и обходится без конгруэнтности и метода суперпозиции. Идеи этого периода, к сожалению, не нашли такого философского изложителя, как Риман или Гельмгольц, а были изложены только техническими математиками. Более того, изменение фундаментальных идей, которое огромно, не вызвало столь же большого изменения в действительной процедуре; поскольку, хотя пространственное количество больше не является частью проективной геометрии, количество все еще используется, и у нас все еще есть уравнения, алгебраические преобразования и так далее. Это может вызвать путаницу, особенно в уме изучающего, который не в состоянии понять, что используемые количества, поскольку предложения действительно проективны, являются простыми названиями точек, а не действительными, как в метрической геометрии. пространственные величины.

Тем не менее, основное отличие этого периода от предыдущего должно сразу бросаться в глаза. В то время как Риман и Гельмгольц имели дело с метрическими идеями и взяли за основу меру кривизны и формулу линейного элемента — обе чисто метрические, — новый метод строится на формулах преобразования координат, необходимых для выражения данной коллинеации. . Он начинает с сведения всех так называемых метрических понятий — расстояния, угла и т. д. — к проективным формам и получает от этого сведения методологическое единство и простоту, прежде невозможные. Эта редукция, однако, зависит, за исключением случаев, когда пространственная постоянная отрицательна, от воображаемых фигур — у Евклида круговые точки находятся в бесконечности; кроме того, он чисто символический и аналитический и должен рассматриваться как неуместный с философской точки зрения. Поскольку вопрос, касающийся значения этой редукции, имеет фундаментальное значение для нашей теории геометрии, и поскольку Кейли в своем президентском обращении к Британской ассоциации в 1883 г. официально призвал философов обсудить использование воображаемых чисел, от которых оно зависит, я будет рассматривать этот вопрос в некоторой степени. Но сначала давайте посмотрим, как с точки зрения математики осуществляется редукция.

31. В течение этого периода мы обнаружим, что почти каждое важное положение, хотя и вводящее в заблуждение в своей очевидной интерпретации, тем не менее, при правильном толковании, имеет широкое философское значение. То же самое и с работой Кейли, пионера проективного метода.

Проективная формула для углов в евклидовой геометрии была впервые получена Лагерром в 1853 г. Эта формула, однако, носила чисто евклидов характер, и Кейли пришлось обобщить ее таким образом, чтобы включить как углы, так и расстояния в евклидову и неевклидовых систем.

Кейли до последнего был убежденным сторонником евклидова пространства, хотя и считал, что неевклидовы геометрии можно применять, в евклидовом пространстве путем изменения определения расстояния. Таким образом, несмотря на свою евклидову ортодоксальность, он снабдил верующих в возможность неевклидовых пространств одним из их самых мощных орудий. В своих «Шестых мемуарах о квантике» (1859 г.) он поставил перед собой задачу «установить понятие расстояния на чисто описательных принципах». Он показал, что при обычном понятии расстояния его можно сделать проективным по отношению к точкам окружности и линии на бесконечности, и что то же самое верно для углов.

Не довольствуясь этим, он предложил новое определение расстояния, как арксинуса или косинуса некоторой функции координат; при таком определении свойства, обычно известные как метрические, становятся проективными свойствами, имеющими отношение к некоторой конике, названной Кейли Абсолютом. (Круговые точки аналитически представляют собой вырожденную конику, так что обычная геометрия образует частный случай вышеизложенного.) Он доказывает, что, когда Абсолют является воображаемой коникой, геометрия, полученная таким образом для двух размеры сферическая Геометрия. Переписка с Лобачевским, в случае, когда Абсолют реален, не проработана: ведь во всем нет никаких свидетельств знакомства с неевклидовыми системами. Важность мемуаров для Кейли полностью заключается в их доказательстве того, что метрическая геометрия является лишь ветвью описательной геометрии.

32. На связь теории расстояния Кэли с метагеометрией впервые указал Кляйн. Клейн подробно показал, что если Абсолют реален, то мы получаем (гиперболическую) систему Лобачевского; если она мнимая, то мы получаем либо сферическую геометрию, либо новую систему, аналогичную системе Гельмгольца, названную Клейном эллиптической; если Абсолют будет воображаемой парой точек, мы получим параболическую геометрию, а если, в частности, пара точек будет круговыми точками, мы получим обычную Евклида. В эллиптической геометрии две прямые на одной плоскости пересекаются только в одной точке, а не в двух, как в системе Гельмгольца. Различие между этими двумя видами геометрии сложно и будет обсуждаться позже.

33. Поскольку все эти системы получены из евклидовой плоскости простым изменением определения расстояния, Кейли и Клейн склонны рассматривать весь вопрос как единое целое, не связанное с природой пространства, а определения расстояния. Поскольку это определение, по их мнению, совершенно произвольно, философская проблема исчезает — евклидово пространство остается в бесспорном владении, и остается только проблема условности и математического удобства. Этот взгляд был настойчиво выражен Пуанкаре: «Что следует думать, — говорит он, — об этом вопросе: верна ли евклидова геометрия? Вопрос — вздор». Геометрические аксиомы, по его словам, являются простыми условностями: они являются «замаскированными определениями». Таким образом, Клейн обвиняет Бельтрами в том, что он рассматривает свой вспомогательный план просто как вспомогательный, и замечает, что, если бы он знал мемуары Кэли, он увидел бы связь между планом и псевдосферой гораздо более тесную, чем он предполагал. Взгляд, полностью удаляющий проблему с арены философии, требует, очевидно, всестороннего обсуждения. К этому обсуждению мы и приступим.

34. Рассматриваемая точка зрения возникла, по-видимому, из-за естественной путаницы в отношении природы используемых координат. Я полагаю, что сторонники этой точки зрения недостаточно осознали, что их координаты — это не пространственные величины, как в метрической геометрии, а простые условные знаки, с помощью которых можно отчетливо обозначить различные точки. Следовательно, пока у нас нет метрической геометрии, нет оснований рассматривать одну функцию координат как лучшее выражение расстояния, чем другую, пока сохраняется основное уравнение сложения. Следовательно, если наши координаты считать адекватными для всей геометрии, то в выражении расстояния возникает неопределенность, которой можно избежать только с помощью соглашения. Но проективные координаты — так будет утверждать наш аргумент — хотя и совершенно адекватны для всех проективных свойств и полностью свободны от какой-либо метрической предпосылки, неадекватны для выражения метрических свойств именно потому, что они не имеют метрической предпосылки. Таким образом, когда речь идет о метрических свойствах, Бельтрами остается оправданным, в отличие от Клейна; сведение метрических свойств к проективным только кажущееся, хотя независимость последних, в отличие от метрической геометрии, совершенно реальна.

35. Но что такое проективные координаты и как они вводятся? Этот вопрос не затрагивался в мемуарах Кейли, и поэтому казалось, что использование координат для определения расстояния связано с логической ошибкой. Ибо координаты во всех предыдущих системах выводились из расстояния; использование любой существующей системы координат для определения расстояния означало, соответственно, замкнутый круг. Кейли упоминает об этом затруднении в примечании, где он, однако, лишь отмечает, что рассматривал свои координаты как числа, произвольно присвоенные в какой-то системе, не исследованной далее, различным точкам. Эту трудность подробно рассмотрел сэр Р. Болл («Теория содержания», Trans. R. I. A. 1889), который настаивает на том, что если значения наших координат уже включают обычную меру расстояния, то дать новое определение, сохранив при этом обычные координаты, вызывает противоречие. Он говорит (указ. соч., стр. 1): «При изучении неевклидовой геометрии я часто чувствовал затруднение, которое, я знаю, разделяли и другие. В этой теории кажется, что мы пытаемся заменить наши обычное понятие расстояния между двумя точками логарифмом некоторого ангармонического отношения. Но само это отношение включает в себя понятие расстояния, измеряемого обычным способом. Как же тогда мы можем заменить наше старое понятие расстояния неевклидовым понятием, поскольку само определение последнего включает в себя первое?"

36. Мы должны признать, что это возражение справедливо до тех пор, пока ангармоническое отношение определяется обычным метрическим способом. Это было бы справедливо, например, против любой попытки найти новое определение расстояния на основе ангармонического отношения Кремоны, в котором оно выступает как метрическое свойство, не измененное проективным преобразованием. Фактически, если нужно избежать логической ошибки, следует избегать любых ссылок на пространственную величину любого рода; ибо вся пространственная величина, как будет показано ниже, логически зависит от фундаментальной величины расстояния. Ангармоническое отношение и координаты должны одинаково определяться чисто описательными свойствами, если их последующее использование должно быть свободным от метрических предпосылок и, следовательно, от возражений сэра Р. Болла.

Такое определение было удовлетворительно дано Кляйном, который для этой цели апеллирует к четырехугольной конструкции фон Штаудта. С помощью этой конструкции, которую я воспроизвел в общих чертах в Главе III. Раздел A, § 112 ff., мы получаем чисто описательное определение гармонического и ангармонического отношения, и, учитывая пару точек, мы можем получить гармоническое сопряжение с любой третьей точкой на той же прямой линии. На этой конструкции основано введение проективных координат. Начиная с любых трех точек на прямой, присвоим им произвольные номера 0, 1, ∞. Затем мы находим гармоническое сопряжение с первым относительно 1, ∞ и присваиваем ему число 2. Цель присвоения этого числа, а не любого другого, состоит в том, чтобы получить значение –1 для ангармонического отношения четырех чисел. соответствует четырем точкам. Затем находим гармонику, сопряженную точке 1 относительно 2, ∞, и присваиваем ей номер 3; и так далее. Кляйн показал, что с помощью этой конструкции мы можем получить любое количество точек и можем построить точку, соответствующую любому заданному числу, дробному или отрицательному. Более того, когда два набора из четырех точек имеют одно и то же ангармоническое отношение, описательно определенное, соответствующие числа также имеют такое же ангармоническое отношение. Вводя такую ​​систему счисления на двух прямых или на трех, мы получаем координаты любой точки на плоскости или в пространстве. Благодаря этой конструкции, имеющей фундаментальное значение для проективной геометрии, удается удовлетворительно избежать логической ошибки, на которой сэр Р. Болл основывает свою критику. Наши координаты вводятся чисто описательным методом и не предполагают никаких предположений относительно измерения расстояния.

37. Таким образом, с этой системой координат определение расстояния как определенной функции координат не является порочным кругом. Но из этого вовсе не следует, что определение расстояния произвольно. Всякое упоминание о расстоянии до сих пор было исключено, чтобы избежать метрических идей; но когда вводится расстояние, неизбежно снова появляются метрические идеи, и мы должны помнить, что наши координаты не дают никакой информации, primâ facie, ни об одной из этих метрических идей. Конечно, мы можем продолжать исключать расстояние в обычном смысле, как количество конечной прямой линии, и определять слово расстояние любым удобным для нас способом. . Но концепция, для которой до сих пор обозначалось это слово, потребует тогда нового названия, и единственным результатом будет смешение кажущегося значения наших предложений для тех, кто сохраняет ассоциации, принадлежащие старое значение слова и реальное значение, вытекающее из нового значения, в котором слово используется.

Я полагаю, что эта путаница действительно имела место в случае тех, кто рассматривает вопрос между Евклидом и метагеометрией как одно из определений расстояния. Расстояние есть количественное отношение и как таковое предполагает тождество качества. Но проективная геометрия имеет дело только с качеством — по этой причине она называется описательной — и не может различить две качественно одинаковые фигуры. Теперь значение качественного подобия в геометрии есть возможность взаимного преобразования посредством коллинеации. Следовательно, любые две пары точек на одной прямой качественно подобны; их единственное качественное отношение — прямая линия, общая для обеих пар; и именно качественное тождество отношений двух пар позволяет исчерпать различие их отношений посредством количества, как различия расстояния. Но там, где количество исключено, любые две пары точек на одной и той же прямой кажутся одинаковыми и даже любые два набора из трех: ведь любые три точки на прямой можно проективно преобразовать в любые другие три. Только с четырьмя точками на линии мы приобретаем проективное свойство, отличающее их от других наборов из четырех, и это свойство является ангармоническим отношением, определяемым описательно.

Таким образом, проективный геометр не видит причины давать имя отношению между двумя точками, поскольку это отношение есть что-либо сверх неограниченной прямой линии, на которой они лежат; и когда он вводит понятие расстояния, он определяет его единственным способом, который позволяют ему определять проективные принципы, как отношение между четырьмя точками. Тем не менее, поскольку он хочет, чтобы слово дало ему возможность различать пары точек, он соглашается взять две из четырех точек как фиксированные. Таким образом, единственными переменными расстояния являются две оставшиеся точки, и поэтому расстояние появляется как функция двух переменных, а именно координат двух переменных точек. Когда мы дополнительно определили нашу функцию так, чтобы расстояние могло быть аддитивным, мы получили функцию со многими свойствами расстояния в обычном смысле. Поэтому проективный геометр считает эту функцию единственным правильным определением расстояния.

Из того, как были введены наши проективные координаты, мы можем видеть, что некоторая функция этих координат должна выражать расстояние в обычном смысле. Ибо они вводились последовательно, так что по мере продвижения от нулевой точки к бесконечной точке наши координаты постоянно росли. Каждой точке соответствовала определенная координата: расстоянию между двумя переменными точками, следовательно, как функции, не зависящей ни от каких других переменных, должна соответствовать некоторая определенная функция координат, так как они сами являются функциями своих точек. Таким образом, рассмотренная выше функция обязательно должна включать расстояние в обычном смысле.

Но произвольный и условный характер расстояния, как утверждают Пуанкаре и Кляйн, возникает из-за того, что две фиксированные точки, необходимые для определения нашего расстояния в проективном смысле, могут быть выбраны произвольно, и хотя, когда наш выбор после того, как сделано, любые две точки имеют определенное расстояние, однако, в зависимости от того, как мы делаем этот выбор, расстояние станет другой функцией двух переменных точек. Введенная таким образом двусмысленность неизбежна с точки зрения проективных принципов; но должны ли мы заключить из этого, что это действительно неизбежно? Не должны ли мы скорее заключить, что проективная геометрия не может адекватно работать с расстоянием? Если A, B, C — три разные точки на прямой, должна быть какая-то разница между отношение A к B и A к C, иначе, в силу качественного тождества всех точек , B и C невозможно различить. Но такое различие включает отношение между A и B, которое не зависит от других точек на линии; ибо, если у нас нет такого отношения, другие точки не могут быть различимы как разные. Следовательно, прежде чем мы сможем различить две неподвижные точки, с которых начинается проективное определение, мы уже должны предположить некоторое отношение между любыми двумя точками на нашей прямой, в котором они независимы от других точек; и это отношение есть расстояние в обычном смысле.

Когда мы измерили это количественное отношение обычными методами метрической геометрии, мы можем приступить к решению, какие исходные точки должны быть выбраны на нашей прямой, чтобы проективная функция, обсуждавшаяся выше, могла иметь то же значение, что и обычное расстояние. Но выбор этих базовых точек, когда мы обсуждаем расстояние в обычном смысле, не произволен, и их введение есть только технический прием. Расстояние в обычном смысле остается отношением между двумя точками, а не между четырьмя; и именно неспособность понять, что проективный смысл отличается от обычного смысла и не может заменить его, породила взгляды Клейна и Пуанкаре. Вопрос не в условности, а в неприводимых метрических свойствах пространства. Подводя итог: количества, используемые в проективной геометрии, не обозначают пространственные величины, а являются условными символами чисто качественных пространственных отношений. Но расстояние, qua количество, предполагает тождество качества, как условие количественного сравнения. Расстояние в обычном смысле есть, короче говоря, такое количественное отношение между двумя точками на прямой, посредством которого можно определить их отличие от других точек. Однако проективное определение, будучи неспособным отличить набор из менее чем четырех точек от любого другого на той же прямой линии, ставит расстояние в зависимость от двух других точек помимо тех, отношение которых оно определяет. Следовательно, для расстояния в обычном смысле не остается имени, и многие проективные геометры, упразднив это имя, полагают, что упраздняется и вещь, и склонны отрицать, что две точки имеют единственное отношение вообще. Эта путаница в проективной геометрии показывает важность имени и должна заставить нас опасаться, чтобы новые значения затемняли одно из фундаментальных свойств пространства.

38. Остается обсудить, каким образом неевклидовы геометрии являются результатом проективного определения расстояния, а также истинную интерпретацию этого взгляда на метагеометрию. Следует заметить, что проективные методы, которые следуют Кэли, во всем имеют дело с евклидовой плоскостью, на которой они вводят различные меры расстояния. Отсюда возникает при любой интерпретации этих методов кажущаяся подчиненность неевклидовых пространств, как если бы они были менее самодостаточны, чем евклидовы. Это подчинение не предполагается в дальнейшем; напротив, корреляция с евклидовым пространством считается ценной, во-первых, потому, что евклидово пространство дольше изучено и более знакомо, а во-вторых, потому что эта корреляция при правильном толковании доказывает, что другие пространства самодостаточны. При обсуждении этой интерпретации мы можем ограничиться, главным образом, расстояниями, измеряемыми по одной прямой. Но мы должны помнить, что метрическое определение расстояния — которое, согласно отстаиваемой здесь точке зрения, является единственным адекватным определением — одинаково в евклидовом и неевклидовом пространствах; аргументировать в его пользу, следовательно, не значит аргументировать в пользу Евклида.

Проекционная схема координат состоит из ряда чисел, каждое из которых представляет определенное ангармоническое отношение и обозначает одну и только одну точку, и которые равномерно увеличиваются с расстоянием от фиксированного начала до тех пор, пока они не станут бесконечными при достижении определенное место. Теперь Кэли показал, что в евклидовой геометрии расстояние может быть выражено как предел логарифма ангармонического отношения двух точек и (совпадающих) бесконечно удаленных точек на их прямой; в то время как, если бы мы предположили, что точки в бесконечности различны, мы получили бы формулу для расстояния в гиперболической или сферической геометрии, в зависимости от того, были ли эти точки реальными или мнимыми. Отсюда следует, что при проективном определении расстояния мы получим именно формулы гиперболической, параболической или сферической геометрии в зависимости от того, как мы выберем точку, которой приписывается значение +∞, на конечном, бесконечном или мнимом расстоянии (в обычном смысле) от точки, которой мы присвоим значение 0. Наша прямая все время остается обычной евклидовой прямой. Но мы видели, что проективное определение расстояния согласуется с истинным определением только тогда, когда две неподвижные точки, к которым оно относится, выбраны соответствующим образом. Теперь в неевклидовых геометриях, как и в евклидовых геометриях, требуется обычное значение расстояния — ведь эти геометрии различаются только метрическими свойствами. Следовательно, наша евклидова прямая, хотя она и может служить для иллюстрации других геометрий, отличных от евклидовой, может быть правильно рассмотрена только Евклидом. Там, где мы даем определение расстояния, отличное от евклидовского, мы все еще находимся в области чисто проективных свойств и не получаем никакой информации о метрических свойствах нашей прямой линии. Но важность этой новой интерпретации для метагеометрии заключается в том, что, установив независимо друг от друга метрические формулы неевклидовых пространств, мы обнаруживаем, как и в «Саджио» Бельтрами, что эти пространства могут быть связаны гомографическим соответствием: с точками евклидова пространства; и что это можно осуществить таким образом, чтобы дать для расстояния между двумя точками нашего неевклидова пространства гиперболическую или сферическую меру расстояния для соответствующих точек евклидова пространства.

39. Таким образом, в целом модификация взгляда сэра Р. Болла, которая является практически обобщенным изложением метода Бельтрами, кажется наиболее обоснованной. Он воображает то, что вместе с Грассманом называет Содержанием, т. е. совершенно общее трехмерное многообразие, а затем сопоставляет его элементы, один за другим, с точками в евклидовом пространстве. Таким образом, каждый элемент Содержания приобретает в качестве своих координат обычные евклидовы координаты соответствующей точки в евклидовом пространстве. Посредством этой корреляции наши вычисления, хотя и относятся к Содержимому, ведутся, как и в Saggio Бельтрами, в обычном евклидовом пространстве. Таким образом, путаница исчезает, но вместе с ней исчезает и предполагаемая евклидова интерпретация. Содержание сэра Р. Болла, если оно вообще должно быть пространством, должно быть пространством, радикально отличным от Евклида; говорить, как это делает Клейн, об обычных плоскостях с гиперболическими или эллиптическими мерами расстояния, значит либо вступать в противоречие, либо отказываться от всякого метрического значения расстояния. Вместо обычных плоскостей у нас есть поверхности, подобные поверхности Бельтрами, с постоянной мерой кривизны; вместо пространства Евклида мы имеем гиперболическое или сферическое пространство. В то же время остается верным, что мы можем с помощью метода Клейна придать евклидово значение каждому символическому предложению в неевклидовой геометрии. Ибо, заменяя расстояние упомянутым выше логарифмом, мы получаем из неевклидова результата результат, который следует из обычных евклидовых аксиом. Это соответствие устраняет раз и навсегда возможность скрытого противоречия в метагеометрии, так как одному предложению в одной соответствует одно и только одно предложение в другой, и поэтому противоречивые результаты в одной системе соответствовали бы противоречивым результатам. в другом. Следовательно, метагеометрия не может привести к противоречиям, если только евклидова геометрия в тот же момент не приводит к соответствующим противоречиям. Таким образом, евклидова плоскость с гиперболической или эллиптической мерой расстояния, хотя она либо противоречива, либо не метрична как независимое понятие, очень полезна при интерпретации неевклидовых результатов.

40. Нам еще предстоит обсудить третий вид неевклидовой геометрии Клейна, который он называет эллиптической. Разницу между этой и сферической геометрией трудно уловить, но ее можно проиллюстрировать более простым примером. Плоскость, как известно, можно без растяжения намотать на цилиндр, и прямые линии на плоскости станут благодаря этой операции геодезическими на цилиндре. Следовательно, геометрии плоскости и цилиндра имеют много общего. Но так как образующая окружность цилиндра, являющаяся одной из его геодезических, конечна, то только часть плоскости расходуется на то, чтобы обернуть ее один раз вокруг цилиндра. Следовательно, если мы попытаемся установить прямое соответствие между плоскостью и цилиндром, мы найдем бесконечный ряд точек на плоскости для одной точки на цилиндре. Так получается, что геодезические, хотя на плоскости они имеют только одну общую точку, на цилиндре могут иметь бесконечное число пересечений. Несколько похоже на это соотношение между сферической и эллиптической геометриями. Каждой точке эллиптического пространства соответствуют две точки сферического пространства. Таким образом, геодезические, которые в сферическом пространстве могут иметь две общие точки, в эллиптическом пространстве никогда не могут иметь более одного пересечения.

Но метод Клейна может только доказать, что эллиптическая геометрия верна для обычной евклидовой плоскости с эллиптической мерой расстояния. Кляйн приложил большие усилия, чтобы усилить различие между сферической и эллиптической геометриями, но не сразу очевидно, что последняя, ​​в отличие от первой, действительна.

Во-первых, эллиптическая геометрия Клейна, которая возникает как одна из альтернативных метрических систем на евклидовой плоскости или в евклидовом пространстве, сама по себе недостаточна, если приведенное выше обсуждение было правильным, чтобы доказать возможность эллиптическое пространство, т.е. пространство, имеющее точечное соответствие с евклидовым пространством и имеющее в качестве обычного расстояния между двумя своими точками эллиптическое определение расстояния между соответствующими точками Евклидово пространство. Чтобы доказать эту возможность, мы должны принять прямой метод Ньюкомба (Crelle's Journal, Vol. 83). Во-первых, Ньюком не доказал самосогласованности своих постулатов; ему только не удалось доказать, что они противоречивы. Это оставило бы эллиптическое пространство в том же положении, в котором Лобачевский и Бойяи оставили гиперболическое пространство. Но дальше, на первый взгляд, в двух-мерном эллиптическом пространстве возникает положительное противоречие. Однако, чтобы объяснить это, потребуется некоторое объяснение особенностей эллиптической плоскости. п

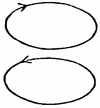
Эллиптическая плоскость, рассматриваемая как фигура в трехмерном эллиптическом пространстве, представляет собой то, что называется двойной поверхностью, т.е. как говорит Ньюкомб (loc. cit. p. 298): «Две стороны полной плоскости не различны, как на евклидовой поверхности... Если... существо должно пройти на расстояние 2D, то по возвращении оно окажется на противоположной поверхности к той, с которой он начал, и ему пришлось бы повторить свое путешествие, чтобы вернуться в исходное положение, не покидая поверхности». Теперь, если мы представим себе двух-мерное эллиптическое пространство, различие между сторонами плоскости становится бессмысленным, так как оно приобретает значение только по отношению к третьему измерению. Тем не менее, какое-то такое различие было бы навязано нам. Предположим, например, что мы взяли небольшой круг, снабженный стрелкой, как на рисунке, и переместили этот круг один раз вокруг вселенной. Тогда смысл стрелки был бы обратным. Таким образом, мы должны были бы быть вынуждены либо считать новое положение отличным от прежнего, превращающего нашу плоскость в сферическую плоскость, либо приписывать обращение стрелки действию движения, возвращающего нашу окружность на ее первоначальное место. Следует отметить, что ничего, кроме движения вокруг вселенной, не достаточно, чтобы изменить направление стрелы. Это обращение похоже на действие пустого пространства, которое заставило бы нас рассматривать точки, которые с трехмерной точки зрения совпадают, хотя и противоположны, как действительно различные, и таким образом уменьшать эллиптическую к сферической плоскости. Но движение, а не пространство, действительно вызывает изменение, и потому не доказано, что эллиптическая плоскость невозможна. Однако этот вопрос не имеет большого философского значения.

41. В связи со сведением метрической геометрии к проективной у нас есть еще одна тема для обсуждения. Это геометрическое использование воображаемых, посредством которых, за исключением случая гиперболического пространства, осуществляется редукция. Я уже утверждал на другом основании, что эта редукция, несмотря на ее огромное техническое значение и несмотря на полную логическую свободу проективной геометрии от метрических идей, является чисто технической, а не философски верный. Тот же вывод появится, если мы примем вызов Кэли в Британской ассоциации в его президентском обращении 1883 года.

В этом выступлении профессор Кейли посвятил большую часть своего времени неевклидовым системам. Он заявил, что неевклидовы пространства кажутся ему ошибочными a priori; но неевклидовы геометрии здесь, как и в его математических работах, были приняты как вытекающие из изменения определения расстояния. Эта точка зрения уже обсуждалась и поэтому не нуждается в дальнейшей критике здесь. Я хочу поговорить о том вопросе, с которого сам Кейли начал свое выступление, а именно о геометрическом использовании и значении мнимых величин. Судя по тому, как он говорил об этом вопросе, необходимо остановиться на нем несколько подробнее. Ибо он сказал (стр. 8–9):

«... Понятие, которое является действительно фундаментальным (и я не могу слишком сильно подчеркнуть это утверждение), лежащим в основе и пронизывающих все понятие современного анализа и геометрии, [является] понятием мнимой величины в анализе и мнимой величины. пространство (или пространство как locus in quo воображаемых точек и фигур) в геометрии: я использую в каждом случае слово воображаемое как включающее в себя реальное... Скажем, даже заключение заключалось в том, что это понятие принадлежит просто техническая математика или имеет отношение к небытиям, относительно которых невозможна никакая наука, тем не менее мне кажется, что (как предмет философского обсуждения) это понятие не следует таким образом игнорировать; следует, по крайней мере, показать, что существует право игнорировать это."

42. Теперь моя цель продемонстрировать это право. Но из опасения, что нематематики не упустят из виду замечание Кэли (которое иногда ошибочно предполагалось относящимся к неевклидовым пространствам), я могу также объяснить с самого начала, что этот вопрос радикально отличается от и лишь косвенно связанные с действительностью или значением метагеометрии. Мнимая величина — это величина, которая включает √–1 : ее наиболее общая форма — a + √–1 b, где a и b настоящие; Кейли использует слово воображаемый, чтобы включить в него реальное, чтобы охватить частный случай, когда b = 0. В дальнейшем будет удобно исключить это более широкое значение и предположить, что b не равен нулю. Воображаемая точка — это точка, координаты которой включают √–1, т. е. координаты которой являются мнимыми величинами. Мнимая кривая — это кривая, точки которой являются мнимыми, или, в некоторых специальных случаях, кривая, уравнение которой содержит мнимые коэффициенты. Нет необходимости здесь обсуждать математические тонкости, к которым приводит это понятие; читатель, который ими интересуется, найдет превосходный элементарный отчет об их геометрическом использовании в «Нихт-Эвклиде» Клейна, II. стр. 38–46. Но для нашей настоящей цели мы можем ограничиться воображаемыми точками. Если обнаружится, что они имеют чисто техническое значение и лишены какого-либо философского смысла, то то же самое относится к любому набору воображаемых точек, то есть к любой воображаемой кривой или поверхности.

Что понятие воображаемых точек имеет первостепенное значение в геометрии, увидит всякий, кто подумает, что круговые точки являются воображаемыми и что сведение метрической геометрии к проективной, являющееся одним из величайших достижений Кэли, зависит от этих точек. . Но адекватно обсудить их философское значение мне трудно, так как я не знаком с какой-либо удовлетворительной философией воображаемого в чистой алгебре. Поэтому я приму наиболее благоприятную гипотезу и предполагаю, что против такого использования нельзя выдвинуть никаких возражений. Я думаю, что даже при этой гипотезе нельзя говорить о мнимых точках в геометрии.

Во-первых, мы должны исключить из рассматриваемых мнимых точек те, координаты которых являются лишь мнимыми с некоторыми специальными системами координат. Например, если одной из координат точки является касательная от нее к сфере, эта координата будет мнимой для любой точки внутри сферы, и все же точка совершенно реальна. Таким образом, точку следует называть мнимой только тогда, когда, какую бы реальную систему координат мы ни приняли, одна или несколько величин, выражающих эти координаты, остаются мнимыми. Для этой цели математически достаточно считать наши координаты декартовыми — точка, декартовы координаты которой являются мнимыми, является истинной мнимой точкой в ​​указанном выше смысле.

Чтобы обсудить значение такой точки, необходимо кратко рассмотреть фундаментальный характер соответствия между точкой и ее координатами. Если предположить, что элементарная геометрия доказала — я думаю, что она действительно доказывает удовлетворительно — что пространственные отношения поддаются количественному измерению, то данная точка будет иметь в подходящей системе координат в пространстве n измерений, n количественных отношений к фиксированной пространственной фигуре, образующей оси координат, и эти n количественные отношения будут, при определенных оговорках, единственными—т.е., никакая другая точка не будет иметь такие же количества, назначенные ей. (При многих возможных системах координат это последнее условие не реализуется: но именно поэтому они неудобны и используются только в специальных задачах.) Таким образом, при заданной системе координат и при любом наборе величин эти величины, если они вообще определяют точку, определяют ее однозначно. Но, естественным расширением метода, указанная выше оговорка снимается и предполагается, что каждому набору величин должна соответствовать некоторая точка. Для этого предположения, мне кажется, нет никаких доказательств. Точно так же почтальон мог бы предположить, что, поскольку каждый дом на улице однозначно определяется своим номером, следовательно, должен быть дом для каждого мыслимого числа. На самом деле мы должны знать, что данный набор величин может быть координатами некоторой точки в пространстве, прежде чем правомерно придавать этим величинам какое-либо пространственное значение: и это знание, очевидно, не может быть получено из операций только с координатами. , под страхом замкнутого круга. Мы должны, возвращаясь к приведенной выше аналогии, знать количество домов на Пикадилли, прежде чем мы узнаем, есть ли у данного числа соответствующий дом или нет; и одна только арифметика, как бы тонко она ни применялась, никогда не даст нам этой информации.

Таким образом, важным является различие не между действительными и мнимыми величинами, а между величинами, которым соответствуют точки, и величинами, которым не соответствуют никакие точки. Можно условно договориться обозначать реальные точки мнимыми координатами, как в гауссовском методе обозначения одной величиной (a + √–1 b) точки, обычные координаты которой являются a, b. Но это не затрагивает смысла Кэли. Кэли имеет в виду, что в математике очень полезно рассматривать в качестве точек, реально существующих в пространстве, предполагаемые пространственные корреляты величин, которые в используемой системе координат не имеют коррелятов в повседневном пространстве; и что эта полезность, по мнению многих математиков, указывает на справедливость столь плодотворного предположения. Чтобы закрепить наши идеи, рассмотрим декартовы оси в трехмерном евклидовом пространстве. Затем при осмотре оказывается, что точка может находиться на любом расстоянии вправо или влево от любой из трех координатных плоскостей; принимая это расстояние за координату, поэтому оказывается, что реальным точкам соответствуют все величины от -∞ до +∞. То же самое происходит и с двумя другими координатами; а поскольку элементарная геометрия доказывает, что их вариации взаимно независимы, мы знаем, что любым трем действительным величинам соответствует одна и только одна реальная точка. Но мы также знаем из применяемого исчерпывающего метода, что все пространство охватывается диапазоном этих трех переменных величин: следовательно, новый набор величин, который вводится с помощью воображаемых величин, не имеет пространственной корреляции и может предполагается, что он обладает им только благодаря удобной фикции.

43. Тот факт, что вымысел удобен, однако, может рассматриваться как указание на то, что это нечто большее, чем вымысел. Но это предположение, я думаю, легко объяснимо. Ибо все плодотворные применения воображаемых в геометрии — это те, которые начинаются и заканчиваются действительными величинами, а воображаемые используются только для промежуточных шагов. Во всех таких случаях мы имеем реальную пространственную интерпретацию в начале и в конце нашего рассуждения, где важна только пространственная интерпретация: в промежуточных звеньях мы имеем дело чисто алгебраическим образом с чисто алгебраическими величинами и можем произвести любые операции, допустимые алгебраически. Если величины, которыми мы заканчиваем, допускают пространственную интерпретацию, тогда и только тогда наш результат можно считать геометрическим. Использование геометрического языка в любом другом случае — лишь удобная помощь воображению. Говорить, например, о проективных свойствах, относящихся к точкам окружности, — это просто memoria technica для чисто алгебраических свойств; точки окружности находятся не в пространстве, а только во вспомогательных величинах, посредством которых преобразуются геометрические уравнения. То, что при геометрической интерпретации воображаемых не возникает никаких противоречий, неудивительно: они интерпретируются исключительно по правилам алгебры, которые мы можем признать действительными в их применении к воображаемым.

Восприятие пространства полностью отсутствует, алгебра господствует, и не может возникнуть никакого противоречия. Везде, где мы позволяем на мгновение вторгнуться нашим обычным пространственным представлениям, возникают грубейшие нелепости — каждый может видеть, что круг, будучи замкнутой кривой, не может уйти в бесконечность. Метафизик, который изобрел бы что-нибудь настолько нелепое, как круглые точки, был бы изгнан с поля. Но математик может безнаказанно украсть лошадь.

Итак, наконец, только знание пространства, а не знание алгебры, может гарантировать нам, что любой заданный набор величин будет иметь пространственный коррелят, а при отсутствии такого коррелята операции с этими величинами не имеют геометрической формы. импорт. Так обстоит дело с воображаемыми в смысле Кэли, и их использование в геометрии, какими бы большими ни были ее технические преимущества, и жесткой, как бы ни была ее техническая достоверность, совершенно лишено философского значения.

44. Теперь, я думаю, мы обсудили большую часть вопросов, касающихся объема и обоснованности проективного метода. Мы видели, что он независим от всех метрических предпосылок и что его использование координат не включает в себя предположение, что пространственные величины измеряются или выражаются ими. Мы видели, что он может одними своими методами решать вопрос о качественном сходстве геометрических фигур, который логически предшествует всякому количественному сравнению, так как количество предполагает качественное сходство. Мы видели также, что в той мере, в какой распространяется его правомерное применение, оно одинаково применимо ко всем однородным пространствам и что его критерий независимо возможного пространства — определение прямой линии двумя точками — не подлежит оговоркам и ограничениям. которые относятся, как мы видели в случае цилиндра, к метрическому критерию постоянной кривизны. Но мы также видели, что, когда проективная геометрия пытается справиться с пространственной величиной и подчинить себе расстояние и измерение углов, ее успех, хотя технически обоснованный и важный, с философской точки зрения является лишь кажущимся успехом. Таким образом, метрическая геометрия, если количество вообще применимо к пространству, остается отдельной, хотя и логически последующей ветвью математики.

45. Осталось сказать несколько слов о Софусе Ли. Как математика, как изобретателя нового и чрезвычайно мощного метода анализа, его нельзя переоценить. Геометрия — лишь один из многих предметов, к которым применима его теория непрерывных групп, но ее применение к геометрии произвело революцию в методе и сделало возможным в таких проблемах, как проблема Гельмгольца, трактовка, бесконечно более точная и исчерпывающая, чем любая другая. было возможно раньше.

Общее определение группы выглядит следующим образом: если у нас есть любое количество независимых переменных x1, x2...xn , и любую серию преобразований этих переменных в новые переменные — преобразования, определяемые уравнениями заданной формы, с параметрами, изменяющимися от одного преобразования к другому — тогда серии преобразований образуют группу, если последовательные применение любых двух эквивалентно одному члену исходного ряда преобразований. Группа является непрерывной, когда мы можем переходить с бесконечно малыми градациями внутри группы от любого одного преобразования к любому другому.

Теперь в геометрии результат двух последовательных движений или коллинеаций фигуры всегда может быть получен посредством одного движения или коллинеации, а любое движение или коллинеация могут быть построены из серии бесконечно малых движений или коллинеаций. Причем аналитическим выражением того и другого является некоторое преобразование координат всех точек фигуры. Следовательно, преобразования, определяющие движение или коллинеацию, таковы, что образуют непрерывную группу. Но вопрос о проективной эквивалентности двух фигур, к которому сводится вся проективная геометрия, всегда должен решаться с помощью коллинеации; и вопрос о равенстве двух фигур, к которому сводится вся метрическая геометрия, всегда должен решаться движением, вызывающим наложение; следовательно, весь предмет геометрии можно рассматривать как теорию непрерывных групп, определяющих все возможные коллинеации и движения.

Итак, Софус Ли очень подробно разработал чисто аналитическую теорию групп; таким образом, при такой постановке задачи у него есть очень сильное оружие, готовое к атаке. В двух работах «Об основаниях геометрии», предпринятых по настоятельной просьбе Клейна, он берет посылки, примерно соответствующие посылкам Гельмгольца, опуская монодромию, и применяет теорию групп к выводу их следствий. Работа Гельмгольца, по его словам, едва ли может рассматриваться как доказательство его выводов, и действительно, более тщательный анализ теории групп открывает несколько возможностей, неизвестных Гельмгольцу. Тем не менее, Гельмгольц как первопроходец, лишённый лживой техники, заслуживает, я думаю, большей похвалы, чем Ли готов дать ему.

Метод Ли совершенно исчерпывающий; опуская посылку монодромии, другие показывают, что тело имеет шесть степеней свободы, т.е. что группа, задающая все возможные движения тела, будет иметь шесть независимых членов; если мы оставим фиксированной одну точку, число независимых членов уменьшится до трех. Затем он, исходя из своей общей теории, перечисляет все группы, удовлетворяющие этому условию. Для того чтобы такая группа давала возможные движения, необходимо, по второй аксиоме Гельмгольца, чтобы она оставляла инвариантной некоторую функцию координат любых двух точек. Это исключает несколько ранее перечисленных групп, каждую из которых он обсуждает по очереди. Таким образом, он пришел к следующим результатам:

I. В двух измерениях, если свободная подвижность должна выполняться универсально, не существует групп, удовлетворяющих первым трем аксиомам Гельмгольца, за исключением тех, которые задают обычные евклидовы и неевклидовы движения. ; но если это должно выполняться только в пределах определенной области, также возможна группа, в которой кривая, описываемая любой точкой вращения, является не замкнутой, а равноугольной спиралью. Чтобы исключить эту возможность, требуется аксиома монодромии Гельмгольца.

II. В трех измерениях результаты еще больше противоречат Гельмгольцу. Предполагая свободную мобильность только в пределах определенного региона, мы должны различать два случая: либо имеет место свободная мобильность внутри этого региона абсолютно без исключения, т.е. когда одна точка закреплена, каждая другая точка внутри области может свободно перемещаться по поверхности: в этом случае аксиома монодромии не нужна, и первых трех аксиом достаточно, чтобы определить нашу группу как евклидовых и неевклидовых движений. Или свободная подвижность в пределах указанной области имеет место только для каждой точки общего положения, а точки определенной линии, когда одна точка зафиксирована, могут только двигаться по этой линии, а не по поверхности: в этом случае возможны другие группы, которые могут быть исключены только четвертой аксиомой Гельмгольца.

Сформулировав теперь чисто математические результаты исследований Ли, мы можем вернуться к философским соображениям, которыми в основном руководствовалась работа Гельмгольца. Становится очевидным не только то, что исключения в пределах определенного региона, но и то, что ограничение на определенный регион аксиомы Свободной Мобильности философски совершенно невозможны и непостижимы. Как может определенная линия или определенная поверхность образовывать в пространстве непреодолимую преграду или иметь какую-либо подвижность, отличную от подвижности всех других линий или поверхностей? Это понятие не может быть допущено в философии ни на мгновение, поскольку оно разрушает самую фундаментальную из всех аксиом — однородность пространства. Следовательно, мы не только можем, но и должны принять аксиому Гельмгольца о свободной мобильности в ее самом строгом смысле; таким образом, аксиома монодромии становится математически, а также философски излишней. Это, с философской точки зрения, самый важный из результатов Ли.

46. Я подошел к концу своей истории метагеометрии. Я не ставил целью дать исчерпывающий отчет даже о важных работах по этому предмету — особенно в третий период имена Пуанкаре, Паша, Кремоны, Веронезе и других, которых можно было бы упомянуть, посрамили бы их. меня, если бы у меня был такой объект. Но я попытался как можно яснее изложить принципы, действовавшие в различные периоды, мотивы и результаты последовательных теорий. Мы видели, как философский мотив, поначалу господствовавший, постепенно вытеснялся чисто математическим и техническим духом новейших геометров. Сначала дискредитация Трансцендентальной Эстетики казалась Метагеометрам столь же важным делом, как и продвижение их науки; но из работ Кэли, Кляйна или Ли ни один читатель не мог понять, что Кант когда-либо жил. Мы также видели, однако, что по мере того, как интерес к философии ослабевал, интерес к философии возрастал: по мере того как математические результаты освобождались от философских споров, они постепенно приобретали устойчивую форму, от которой дальнейшее развитие, как мы можем с полным основанием надеяться, примет форму роста, а не трансформации. Я полагаю, что такое же постепенное развитие философии можно проследить в зачаточном состоянии большинства разделов математики; когда философские мотивы перестают действовать, это вообще есть признак того, что стадия неопределенности в отношении посылок пройдена, так что будущее всецело принадлежит математической технике. Когда эта стабильная стадия достигнута, наступает время для философии заимствовать у науки, принимая ее окончательные посылки как навязанные реальной необходимостью факта или логики.

47. Теперь, обсуждая системы метагеометрии, мы обнаружили два вида, радикально отличающиеся друг от друга и подчиняющиеся разным аксиомам. Исторически предшествующий тип, имеющий дело с метрическими идеями, прежде всего обсуждает условия Свободной Подвижности, которая существенна для всякого измерения пространства. Аналитическое выражение этих условий она находит в существовании пространственно-постоянной, или постоянной меры кривизны, эквивалентной однородности пространства. Это его первая аксиома.

Его вторая аксиома гласит, что пространство имеет конечное целое число измерений, т. е. в метрических терминах положение точки относительно любой другой фигуры в пространстве однозначно определяется конечным числом измерений. количество пространственных величин, называемых координатами.

Третью аксиому метрической геометрии можно назвать, чтобы отличить ее от соответствующей проективной аксиомы, аксиомой расстояния. Существует, говорит он, одно отношение между любыми двумя точками, которое может сохраняться неизменным при совместном движении обеих точек и которое всегда остается неизменным при любом движении системы как одного твердого тела. Это отношение мы называем расстоянием.

Приведенное выше утверждение трех основных аксиом метрической геометрии взято из Гельмгольца с поправками, внесенными Ли. Собственная формулировка аксиом Ли, как цитировалось выше, находилась под слишком сильным влиянием проективных методов, чтобы дать исторически правильную передачу духа второго периода; Утверждение Гельмгольца, напротив, требует, как показал Ли, очень значительных модификаций. Таким образом, я надеюсь, что приведенный выше компромисс может быть воспринят как принятие поправок Ли при сохранении духа Гельмгольца.

48. Но метрическая геометрия, хотя она исторически предшествует, логически следует за проективной геометрией. Ибо проективная геометрия имеет дело непосредственно с тем качественным сходством, которого требует в качестве своего основания суждение количественного сравнения. Теперь три приведенные выше аксиомы метрической геометрии, как мы увидим в главе III. Раздел Б не предполагает измерения, а, наоборот, представляет собой условия, предполагаемые измерением. Без этих аксиом, общих для всех трех пространств, измерение было бы невозможно; с ними, как я утверждаю, измерение способно, хотя и только эмпирически, решить приблизительно, какое из трех пространств действительно для нашего действительного мира. Но если сами эти три аксиомы выражают не результаты, а условия измерения, то не должны ли они быть эквивалентны утверждению о том качественном сходстве, от которого зависит количественное сравнение? И если так, то не должны ли мы ожидать найти те же самые аксиомы, хотя, возможно, в другой форме, в проективной геометрии?

49. Это ожидание не будет обмануто. Вышеупомянутые три аксиомы, как мы увидим далее, все без исключения философски эквивалентны однородности пространства, а это, в свою очередь, эквивалентно аксиомам проективной геометрии. Фактически аксиомы проективной геометрии можно грубо сформулировать так:

Я. Пространство непрерывно и бесконечно делимо; ноль протяженности, возникающий в результате бесконечного деления, называется Точкой. Все точки качественно подобны и отличаются тем, что лежат вне друг друга.

II. Любые две точки определяют уникальную фигуру, прямую линию; две прямые линии, как и две точки, качественно подобны и отличаются тем, что являются взаимно внешними.

III. Три точки не на одной прямой определяют единственную фигуру, плоскость, а четыре точки не на одной плоскости определяют трехмерную фигуру. Этот процесс может быть, насколько можно видеть а priori, продолжен, никоим образом не мешая возможности проективной геометрии, до пяти или до n точек. Но проективная геометрия требует в качестве аксиомы, чтобы процесс останавливался с некоторым положительным целым числом точек, после чего любая новая точка содержится в фигуре, определяемой уже данными. Если процесс останавливается с (n + 1) точками, говорят, что наше пространство имеет n измерений.

Эти три аксиомы, как будет видно, являются эквивалентами трех аксиом метрической геометрии, выраженными без ссылки на количество. Мы обнаружим, что они, как и раньше, выводимы из однородности пространства или, еще шире, из возможности переживания внешнего. Следовательно, они будут казаться априорными, необходимыми для существования любой геометрии и для восприятия внешнего мира как такового.

50. То, что в этих аксиомах заключена некоторая логическая необходимость, может быть, я думаю, выведено как вероятное только из их исторического развития. Ибо системы метагеометрии в целом не были установлены как более подходящие для фактов, чем система Евклида; за исключением, например, Целльнера, я не знаю никого, кто считал бы четвертое измерение необходимым для объяснения явлений. Что касается опять-таки пространственной постоянной, хотя малая пространственная постоянная считается эмпирически возможной, она обычно не считается вероятной; а конечные пространственные константы, с которыми в равной степени знакома метагеометрия, обычно не считаются даже возможными в качестве объяснения эмпирических фактов. Таким образом, мотивом всегда был не факт, а логика. Не дает ли это сильного предположения, что те аксиомы, которые сохраняются, сохраняются потому, что они логически необходимы? Если это так, то аксиомы, общие для Евклида и метагеометрии, будут априорными, а аксиомы, присущие Евклиду, будут эмпирическими. После критики некоторых различных теорий геометрии я продолжу в главах III. и IV., к доказательству и следствиям этого тезиса, которые составят оставшуюся часть настоящей работы.

---

О серии книг HackerNoon: мы предлагаем вам самые важные технические, научные и содержательные общедоступные книги.

Эта книга является общественным достоянием. Бертран Рассел. (1897 г.). ОПИСАНИЕ ОСНОВ ГЕОМЕТРИИ. Урбана, Иллинойс: Проект Гутенберг. Получено в июне 2022 г. с https://www.gutenberg.org/cache/epub. /52091/pg52091-images.html.

Эта электронная книга предназначена для использования кем угодно и где угодно бесплатно и почти без каких-либо ограничений. Вы можете копировать ее, отдавать или повторно использовать в соответствии с условиями лицензии Project Gutenberg, прилагаемой к этой электронной книге, или в Интернете по адресу www.gutenberg.org. , расположенный по адресу https://www.gutenberg.org/policy/license.html.< /эм>

---

Оригинал