Эволюция деревьев решений: от энтропии Шеннона к современным приложениям и специальностям

Как это началось…

Путь к выигрышному подходу Kaggle начался в середине 20 века, и с тех пор его разработка претерпела ряд усовершенствований и улучшений:

1. Раннее начало (1950–1960-е годы). Основу алгоритмов дерева решений можно проследить до разработки теории информации Клодом Шенноном в 1940-х годах (статья 1948 года "A Mathematical Theory_of_Communication", а также упоминается как энтропия Шеннона - она ​​стала одной из наиболее часто используемых примесей. Критерии разделения узлов. Идея использования древовидной структуры со встроенной функцией получения информации для принятия решений была вдохновлена ​​этой основополагающей работой.

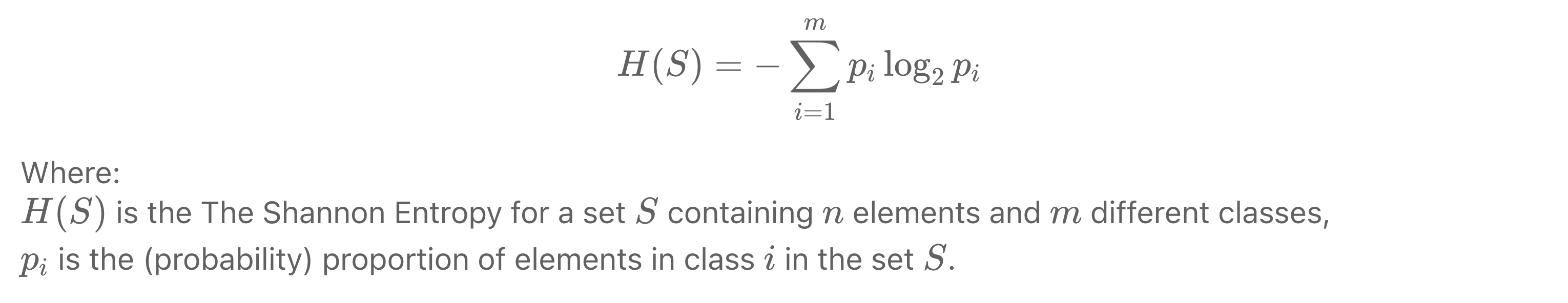
1. Разработка ключевых алгоритмов (1960–1980-е годы). В 1960–1970-х годах исследователи разработали несколько ключевых алгоритмов дерева решений.

Некоторые из наиболее примечательных включают: * Хи-квадрат автоматического обнаружения взаимодействия (CHAID) — Гордон В. Касс разработал алгоритм CHAID в 1980 году. CHAID использует критерий хи-квадрат для измерения значимости связи между входными объектами и целевой переменной.

• Итеративный дихотомайзер 3 (ID3). Росс Куинлан, ученый-компьютерщик, представил алгоритм ID3 в 1986 году. ID3 использует жадный нисходящий подход и выбирает лучший атрибут для разделения набора данных на основе получения информации.

1. Деревья классификации и регрессии (CART). Лео Брейман, Джером Фридман, Ричард Олшен и Чарльз Стоун представили алгоритм CART в 1984 году. CART использует индекс примесей Джини для выбора оптимального разделения и может обрабатывать обе классификации и задачи регрессии.

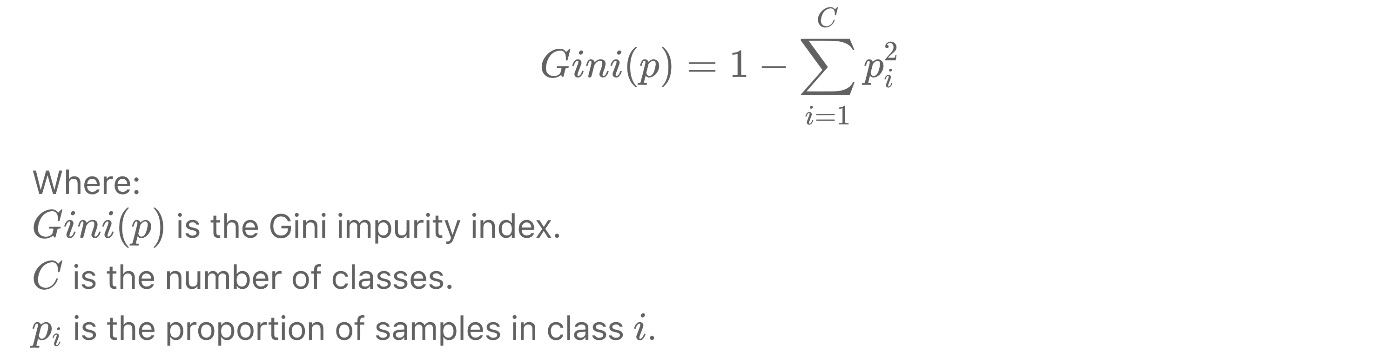
1. C4.5 — Росс Куинлан улучшил алгоритм ID3, представив алгоритм C4.5 в 1993 году. В версии 4.5 были устранены некоторые ограничения ID3, такие как переобучение, обработка непрерывных функций и обрезка дерева для уменьшения его сложности, с использованием нормализованного прироста информации (коэффициент усиления) и распределения экземпляров отсутствующих значений среди всех дочерних узлов, но с уменьшенными весами, пропорциональными количеству экземпляров от каждого дочернего узла.

Алгоритм

Идея и псевдореализация

Он работает путем рекурсивного разделения набора данных на подмножества на основе поиска наилучшего разделения с точки зрения максимизации прироста информации, что в конечном итоге создает древовидную структуру.

В качестве примера, вот упрощенная версия алгоритма ID3 в псевдокоде:

def build_tree(data, depth=0, max_depth=None):
    # Create a node t
    t = Node()

    # Check the stopping criterion
    if stopping_criterion(data, depth, max_depth):
        # Assign a predictive model (majority class) to t
        t.predictive_model = majority_class(data)
    else:
        # Find the best binary split: data = data_left + data_right
        feature, threshold, data_left, data_right = best_binary_split(data)

        # Assign the chosen feature and threshold to the node
        t.feature = feature
        t.threshold = threshold

        # Recursively build the left and right subtrees
        t.left = build_tree(data_left, depth + 1, max_depth)
        t.right = build_tree(data_right, depth + 1, max_depth)

    return t

Со следующими функциями в соответствии с конкретными требованиями:

1. Node()>: класс или функция для создания объекта узла дерева.

2. stopping_criterion(data, depth, max_depth): функция, определяющая, когда прекратить разбиение дерева. Он должен принимать текущие данные, текущую глубину и дополнительную максимальную глубину в качестве входных данных и возвращать логическое значение.

3. majority_class(data): функция для назначения основного класса (или другой подходящей модели) конечному узлу с учетом данных.

4. best_binary_split(data): функция, которая принимает данные в качестве входных данных и возвращает лучший признак, пороговое значение и два результирующих набора данных (левый и правый) после разделения на основе критерия примеси и функциональности.< /p>

Современное использование и визуализация благодаря scikit-learn

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier,plot_tree
clf = DecisionTreeClassifier(random_state=0)
iris = load_iris()
cross_val_score(clf, iris.data, iris.target, cv=10)
plt.figure(figsize=(12, 8))
plot_tree(clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names)
plt.show()

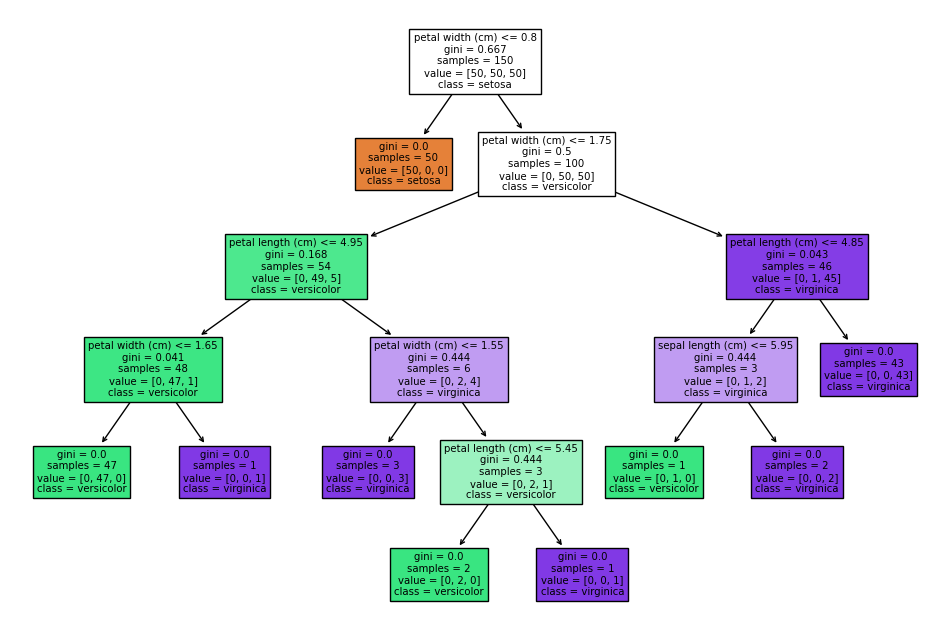
Использовать особенности

Алгоритм дерева решений особенно подходит для обработки структурированных данных и имеет несколько особенностей, которые делают его привлекательным для различных вариантов использования:

1. Интерпретируемость. Деревья решений легко понять и интерпретировать, поскольку они имитируют процессы принятия решений человеком, разбивая сложные решения на более простые. Древовидная структура интуитивно понятна и может быть визуализирована, что упрощает понимание логики модели пользователями, не являющимися техническими специалистами.

2. Обработка смешанных типов данных. Деревья решений могут обрабатывать как категориальные, так и числовые данные без необходимости предварительной обработки или преобразования. Эта гибкость делает его удобным для реальных наборов данных, которые часто содержат данные разных типов.

3. Выбор функций. Деревья решений выполняют неявный выбор функций в процессе обучения, выбирая наиболее важные функции для разделения данных. Это помогает снизить сложность модели и улучшить ее интерпретируемость.

4. Непараметрические. Деревья решений — это непараметрические алгоритмы, то есть они не делают никаких предположений о базовом распределении данных. Это делает их более устойчивыми к выбросам и позволяет моделировать сложные отношения между объектами и целевой переменной.

5. Масштабируемость. Алгоритмы дерева решений можно легко масштабировать для обработки больших наборов данных, особенно при использовании таких методов оптимизации, как обрезка или случайный лес, которые объединяют несколько деревьев для повышения общей производительности.

6. Нечувствительность к монотонным преобразованиям: деревья решений не зависят от монотонных преобразований входных признаков, таких как масштабирование или нормализация. Это упрощает этапы предварительной обработки и снижает риск появления ошибок при подготовке данных.

7. Простота проверки. Деревья решений можно легко проверить с помощью статистических тестов для оценки качества разделения, что обеспечивает дополнительный уровень уверенности в производительности модели.

8. Обработка отсутствующих значений. Алгоритмы дерева решений могут обрабатывать отсутствующие данные с помощью таких стратегий, как суррогатное разделение, которое находит альтернативные критерии разделения, когда отсутствуют данные для основного атрибута.

Почему деревья так важны и где их найти

Алгоритм дерева решений классифицируется вместе с другими менее мощными моделями, такими как линейная/логистическая. регрессия, KNN и SVM из-за присущих им ограничений:

* Склонен к переоснащению * Чувствителен к небольшим изменениям данных * Может создавать предвзятые деревья, если некоторые классы доминируют

Тем не менее, величие и мощь фундаментов Дерева решений, как и их подлинных аналогов, действительно раскрываются в сложных ансамблях и важных деталях:

1. Изолирующие леса. Изолирующие леса, основанные на деревьях изоляции, представляют собой метод обнаружения аномалий. Они используют уникальный подход к построению деревьев решений путем случайного выбора функций и разделенных значений, что позволяет изолировать выбросы быстрее, чем обычные экземпляры.

Структура дерева решений имеет решающее значение для эффективного обнаружения аномалий этим методом.

* Как они устроены * Случайным образом выберите функцию и разделите значение между минимальным и максимальным значениями выбранной функции.

   
 * Recursively partition the data based on the split value until all instances are isolated or a predefined tree depth is reached.

   
 * Repeat the process to build multiple trees, forming an Isolation Forest.

   
 * Calculate anomaly scores for each instance by averaging the path length (number of splits) across all trees in the forest.

   

• Преимущества по сравнению с одним деревом решений:

  • Более устойчив к шуму. Изолированные леса менее восприимчивы к шуму, поскольку они построены с использованием случайных разбиений.

  * Эффективное обнаружение аномалий: они могут обнаруживать аномалии быстрее, чем одно дерево решений, благодаря своему механизму изоляции.

  * Уменьшение переобучения: ансамбль деревьев в изолированном лесу снижает риск переобучения по сравнению с одним деревом.

  2. Случайные леса: случайные леса представляют собой ансамбль деревьев решений, которые строятся путем начальной загрузки набора данных и выбора случайных подмножеств признаков в каждом узле. Этот метод уменьшает переоснащение и улучшает обобщение по сравнению с одним деревом решений. Алгоритм дерева решений служит строительным блоком для каждого дерева в ансамбле.

* Как они устроены: * Создайте несколько образцов начальной загрузки (с заменой) из исходного набора данных. * Для каждой начальной загрузки постройте дерево решений, выбрав случайное подмножество функций в каждом узле и выбрав наилучшее разделение. * Объедините деревья, усредняя их прогнозы для задач регрессии или получив большинство голосов для задач классификации.

• Преимущества по сравнению с одним деревом решений:

  • Повышенная точность. Случайные леса обычно дают лучшие результаты из-за разнообразия деревьев в ансамбле.

  * Уменьшение переобучения: процесс начальной загрузки и выбора функций снижает риск переобучения.

  * Улучшенная обработка несбалансированных данных. Случайные леса могут сбалансировать распределение классов, используя веса классов или за счет избыточной выборки недопредставленных классов. * Устойчивость к шуму: ансамблевый подход делает случайные леса более устойчивыми к шуму и выбросам.

  3. Ускоренные деревья. Методы повышения эффективности итеративно создают ансамбль деревьев решений. Каждое дерево обучается исправлять ошибки, допущенные предыдущим деревом. Алгоритм дерева решений является основным методом обучения в этих моделях, и его способность фиксировать сложные отношения и взаимодействия является ключом к успеху этих методов.

* Как они устроены: * Инициализируйте модель с постоянным значением прогноза. * Для предопределенного количества итераций: * Вычислить отрицательные градиенты (псевдо-остатки) функции потерь по отношению к прогнозам текущей модели. * Сопоставьте дерево решений с псевдоостатками. * Обновите модель, добавив новое подогнанное дерево, умноженное на скорость обучения. * Объедините деревья, просуммировав их взвешенные прогнозы.

• Преимущества по сравнению с единым деревом решений:

  • Более высокая точность. Ускоренные деревья часто обеспечивают более высокую производительность благодаря повторяющемуся процессу исправления ошибок, допущенных предыдущими деревьями.

  * Уменьшение переобучения. Методы регуляризации, такие как сокращение (скорость обучения) и ранняя остановка, помогают предотвратить переоснащение.

  * Улучшенная обработка несбалансированных данных: Boosted Trees может справляться с несбалансированностью классов, корректируя функцию потерь или применяя взвешивание экземпляров.

  * Гибкость: Boosted Trees могут работать с различными функциями потерь, что делает их подходящими для разных задач (например, классификации, регрессии, ранжирования).

  4. Важность признаков. Основная цель определения важности признаков – ранжировать переменные в наборе данных на основе их вклада в точность прогноза или получение информации.

Эта информация может быть преобразована в: * интерпретация модели с объяснением обоснования ее прогнозов с раскрытием данных, лежащих в основе

• выбор функций с определением наиболее релевантных функций в наборе данных, что позволяет разрабатывать более простые и эффективные модели

В заключение

Дерева решений прошли долгий путь с момента их появления в 1960-х годах. Их универсальность, интерпретируемость и способность обрабатывать различные типы данных сделали их популярным выбором для различных приложений во многих областях. В то время как автономные деревья решений могут страдать от ограничений, таких как переоснащение и чувствительность к небольшим изменениям данных, их истинный потенциал используется в методах ансамбля, таких как изолированные леса, случайные леса и усиленные деревья. Эти передовые методы используют возможности деревьев решений для повышения точности, надежности и универсальности и стали самыми популярными методами от Kaggle до корпоративной разработки. По мере того, как машинное обучение продолжает развиваться, понимание и использование этих вечных классических методов будет оставаться бесценным как для исследователей, так и для практиков в этой области.