
Неуловимое изобилие первичных черных дыр
3 сентября 2024 г.Авторы:
(1) Антонио Риотто, Департамент теоретической физики, Женевский университет, набережная Ансермет, 24, CH-1211 Женева 4, Швейцария и Центр науки о гравитационных волнах (GWSC), Женевский университет, CH-1211 Женева, Швейцария;
(2) Джо Силк, Институт астрофизики, UMR 7095 CNRS, Университет Сорбонны, 98bis Bd Arago, 75014 Париж, Франция, Кафедра физики и астрономии, Университет Джонса Хопкинса, Балтимор, Мэриленд, 21218, США, и Институт астрофизики элементарных частиц и космологии Бикрофта, Кафедра физики, Оксфордский университет, Оксфорд, OX1 3RH, Великобритания.
Таблица ссылок
Аннотация и 1 Введение
2 Некоторые открытые вопросы
2.1 Какова распространенность ПГБ?
2.2 Каков эффект кластеризации PBH?
2.3 Какую часть наблюдаемых в настоящее время событий ГВ можно отнести к ПЧД?
2.4 Являются ли PBH темной материей?
3. Дорожная карта PBH
3.1 Слияния с высоким красным смещением
3.2 PBH-системы с субсолнечной энергией
3.3 Заполнение пробела в парной нестабильности с помощью PBH?
3.4 Эксцентриситет PBH, 3.5 Вращение PBH и 3.6 Будущие гамма-телескопы
4 Выводы и ссылки
2.1 Какова распространенность ПГБ?
Образование PBH в ранней Вселенной — редкое событие, и знание точной вероятности образования представляет собой, даже в наши дни, сложную задачу. Этот вопрос имеет фундаментальное значение, поскольку вероятность образования — один из ключевых компонентов для расчета текущего содержания PBH и функции массы, которые не только входят во многие наблюдаемые, такие как скорость слияния двойных BH, но и которые также обычно используются для выражения текущих ограничений из различных наблюдений.
Чтобы проиллюстрировать сложность оценки точного содержания PBH, рассмотрим наиболее стандартный сценарий в литературе, где PBH образуются в результате коллапса крупных неоднородностей, образующихся на стадии инфляции. Последний дает стохастическую величину, возмущение кривизны ζ на масштабах сверхгоризонта, свойства которого известны статистически. Как мы уже упоминали, PBH являются редкими событиями, требующими, чтобы заданная наблюдаемая величина, например, контраст плотности δ или функция уплотнения C, была выше типично большого критического значения. Это подразумевает, что расчет содержания PBH требует выхода за рамки линейной теории возмущений и знания хвоста вероятности, где последний, как правило, далек от простого гауссовского распределения. Нелинейности вступают в игру, даже когда начальное возмущение кривизны является гауссовым (что, как правило, не так) из-за нелинейной связи между функцией избыточной плотности/уплотнения и самим возмущением кривизны. Логическая цепочка (в излучении) такова:

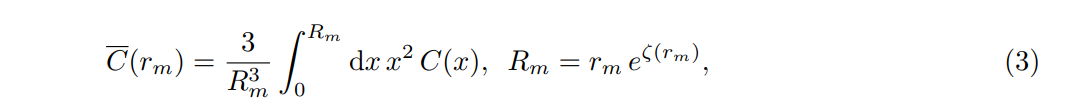
но до сих пор в литературе нет расчетов и нет понимания того, почему объемное среднее функции уплотнения имеет критический порог, который не зависит от профиля. Даже без необходимости упоминания других возможных проблем, например, работы с нелинейностями, входящими в функцию передачи излучения, когда возмущения повторно входят в горизонт [3] или необходимости иметь дело с явлением смешивания операторов [4], мы считаем, что расчет распространенности PBH в стандартном сценарии все еще остается открытым вопросом, который заслуживает дальнейшего изучения. То же самое верно и для альтернативных механизмов генерации PBH, например, в переохлажденных фазовых переходах первого рода [5], где пороговый критерий недостаточен.
Эта статьядоступно на arxivпо лицензии CC BY 4.0 DEED.
Оригинал

