Погрузитесь в Verkle Tree для Ethereum

По сравнению с Merkle Tree, Verkle Tree был значительно улучшен в размере Proof, что является важной частью обновления ETH2.0. Когда дело доходит до данных размером в один миллиард, доказательство дерева Меркла займет 1 КБ, в то время как доказательство дерева Веркла требует не более 150 байт.

Концепция Verkle Tree была предложена в 2018 году (более подробную информацию можно найти [здесь] (https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf). 23-й технический обзор Sin7Y продемонстрирует принцип Verkle Tree.

Дерево Меркла

Прежде чем углубляться в Verkle Tree, важно понять концепцию Merkle Tree. Дерево Меркла — это обычный аккумулятор, который можно использовать для доказательства существования одного элемента в аккумуляторе, как показано на следующем рисунке:

![Рисунок 1: Дерево Меркла] (https://cdn.hackernoon.com/images/Ns6mVt8NqgNkfsouVyus9tAe3mB2-yzb3ksz.png)

Чтобы доказать, что (ключ: значение) = (06: 32) существует в Дереве (отмечено зеленым), Доказательство должно содержать все отмеченные красным узлы на рисунке.

Верификатор может вычислить корень в соответствии с методом, показанным на рисунке 1, а затем сравнить его с ожидаемым корнем (отмечен серым цветом).

Можно предсказать, что с увеличением глубины и ширины дерева размер Proof также будет больше (для разветвленного-2 сложность составляет log_2(n), а для разветвленного-k — (k− 1)log_k(n).

Кроме того, верификатору необходимо провести большое количество вычислений хэша от базового уровня до верхнего уровня. Таким образом, увеличение глубины и ширины Дерева приводит к увеличению нагрузки на верификатора, что недопустимо.

Дерево Веркле - Концепция

Простое увеличение ширины дерева может уменьшить его глубину, но размер доказательства не уменьшится, поскольку размер доказательства изменится с исходного log_2(n) на (k−1)log_k(n).

То есть для каждого уровня доказывающая сторона должна предоставить (k−1) дополнительную информацию об узле. В статье Verkle Tree Джон Кузмаул упомянул схему уменьшения сложности доказательства до logk(n).

Если мы установим k=1024, доказательство уменьшится на log_2(k) = 10 раз.

Дизайн Verkle Tree показан следующим образом:

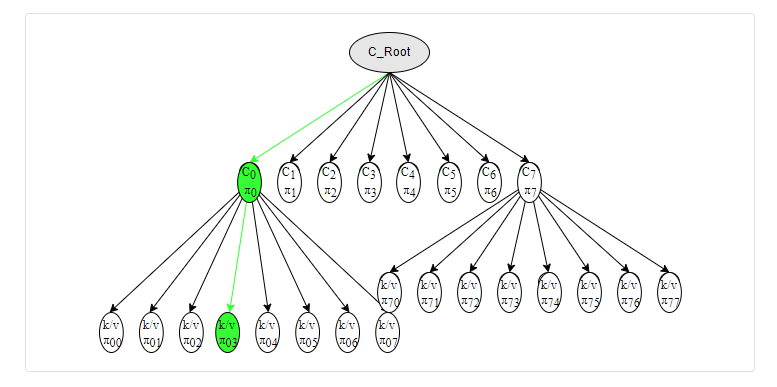
Для каждого узла есть две части информации: (1) значение; (2) доказательство существования π. Например, отмеченный зеленым цветом (H(k,v),π_03) показывает, что H(k,v) существует в обязательстве C_0 и π_03 является доказательством этого аргумента.

Точно так же (C_0,π_0) означает, что C_0 существует в фиксации C_Root и π_0 является доказательством этого аргумента.

В статье Verkle Tree метод такой фиксации существования называется [Векторная приверженность] (https://eprint.iacr.org/2011/495.pdf). Если для выполнения обязательства существования исходных данных используется схема подтверждения «Вектор», будет получено доказательство со сложностью O(1), в то время как сложность доказательства построения и доказательства обновления составляет O(n^2),O (н) соответственно.

Поэтому для достижения баланса в статье «Дерево Веркле» используется K-арная схема дерева Веркле (как показано на рисунке 2), чтобы сделать сложность построения доказательства, обновления доказательства и доказательства равной O(kn),O(klogk n),O(logk n) соответственно.

Конкретное сравнение производительности показано в таблице 1:

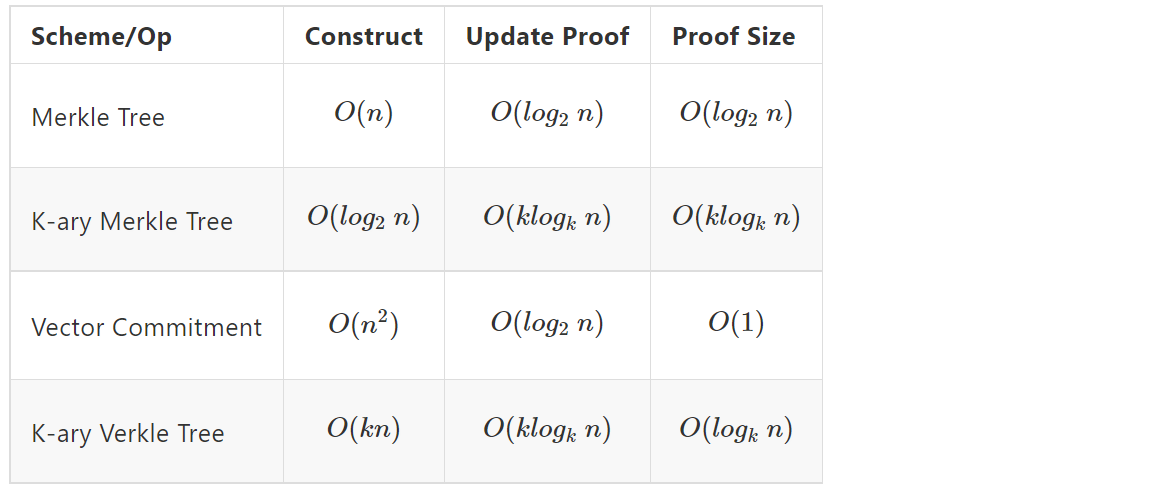
В этой статье мы не собираемся давать подробное введение в некоторые конкретные схемы коммитирования векторов, которые Джон Кушмаул хорошо объяснил в своей статье.

К счастью, по сравнению с векторным обязательством у нас есть более эффективный инструмент, называемый полиномиальным обязательством.

Учитывая группу набора координат (c_0,c_1,....,c_n) и набор значений (y_1,y_2,....,y_n), вы можете построить многочлен ([интерполяция Лагранжа] (https://en.wikipedia.org/wiki/Lagrange_polynomial)), удовлетворяющих  P(c_i)=y_i, и выполнить обязательство по этому полиному.

KZG10 и IPA являются обычным многочленом схемы фиксации (в этот момент обязательство представляет собой точку на эллиптической кривой, обычно размером от 32 до 48 байтов).

Основа

KZG для одной точки

Возьмите KZG10 в качестве примера. Для полинома P(x) мы используем [P(s)]_1 для представления полиномиального обязательства.

Как мы все знаем, для P(x), если P(z)=y, то (x−z)|(P(x)−y). То есть, если мы установим * Q(x)=(P(x)−y)/(x−z), тогда Q(x)* является полиномом.

Теперь мы создаем доказательство для P(x)P(x), чтобы удовлетворять P(z)=yP(z)=y. То есть вычислите [Q(s)]1[Q(s)]1 и отправьте его верификатору, которому нужно проверить:

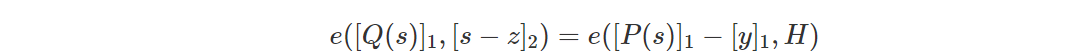
Поскольку s является случайно выбранной точкой в ​​конечной области F, вероятность успешного злонамеренного поведения доказывающего равна степени (Q)/P (лемма Шварца-Циппеля).

KZG для нескольких точек

Теперь мы хотим доказать, что значения полинома P(x) на (z0,z1,....,zk−1) равны (y1,y2,....,yk−1 ), соответственно. Следовательно, нам нужно определить два полинома:

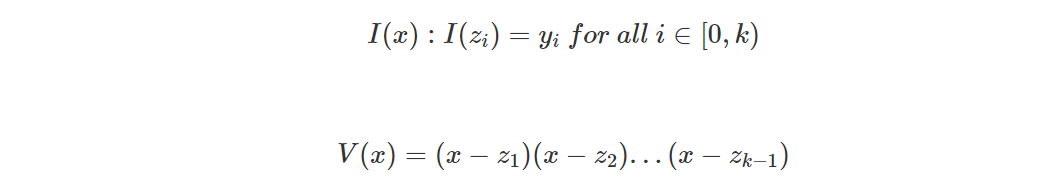
Согласно описанию, упомянутому выше, нам необходимо удовлетворить V(x)|(P(x)−I(x)). То есть существует многочлен Q(x) , удовлетворяющий:

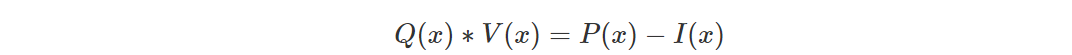
Следовательно, доказывающему необходимо предоставить обязательства [P(s)]_1,[Q(s)]_1 для P(x) и Q(x) и отправить обязательства на верификатор.

Verifier вычисляет [I(s)]_1,[V(s)]_2 локально и проверяет уравнение:

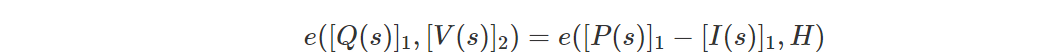
Ясно, что размер доказательства не зависит от количества точек. Если мы выберем кривую BLS12-381, размер Proof составит всего 48 байт, что очень эффективно.

Дерево Веркле – ETH

По сравнению с деревом Меркла, в котором для доказательства существования элемента доказывающему по-прежнему необходимо предоставить доказательство размером O(log_2n) , в дереве Веркла значительно улучшен размер доказательства.

Давайте рассмотрим простой пример Verkle Tree.

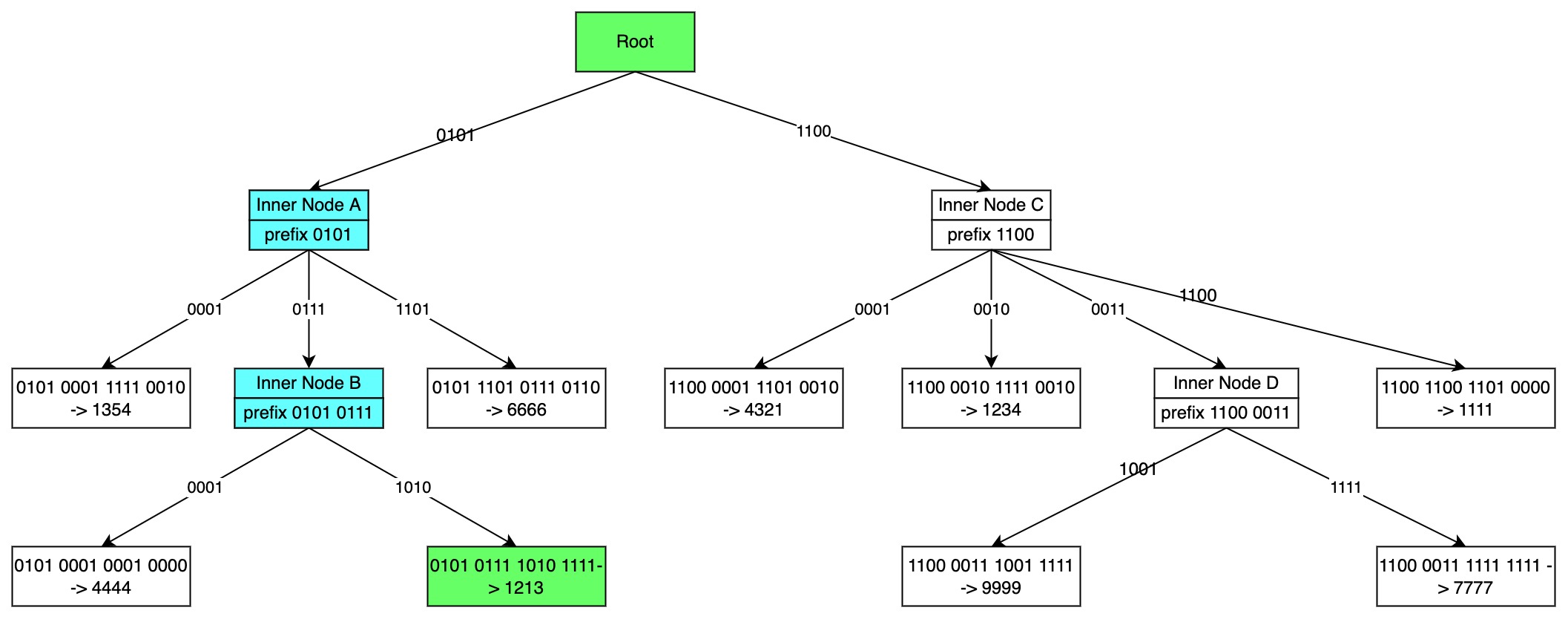
Видно, что, подобно структуре дерева Меркла Патриции, узлы можно разделить на три типа — пустой узел, внутренний узел и листовой узел.

Ширина каждого внутреннего дерева узлов равна 16 (0000->1111 в шестнадцатеричном формате). Чтобы доказать, что состояние листового узла равно (0101 0111 1010 1111 -> 1213), нам нужно провести коммит на внутренний узел A и внутренний узел B:

1. Докажите, что значение обязательства внутреннего узла B равно хэшу (0101 0111 1010 1111, 1213) с индексом 1010.

1. Докажите, что значение обязательства внутреннего узла A равно хэшу (cm_B) с индексом 0111.

1. Докажите, что значение обязательства узла Root равно хешу (cm_A) с индексом 0101;

Используйте C_0(InnernodeB),C_1(InnernodeA),C_2(Root) для представления обязательств, упомянутых выше, и соотнесите их с полиномом f_i(x) соответственно.

Таким образом, доказывающему необходимо доказать:

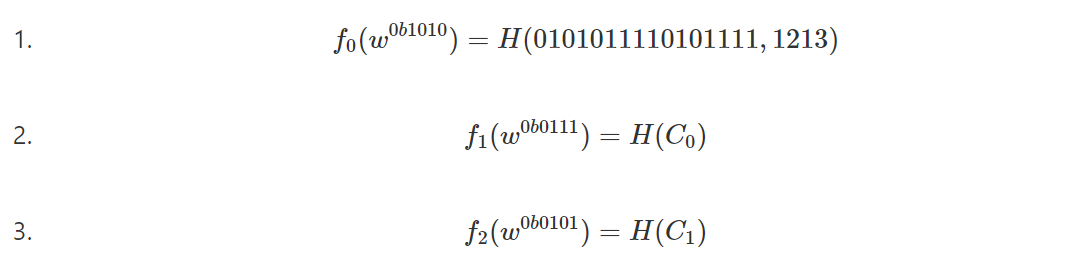
Сжатие для нескольких полигонов

Для простоты мы будем использовать z_i для представления индекса.

Доказывающему необходимо доказать, что для множества полиномов f_0(x),f_1(x),....,f_m−1(x) оно удовлетворяет следующим условиям в точках z_0,z_1,.... ,z_m−1 соответственно:
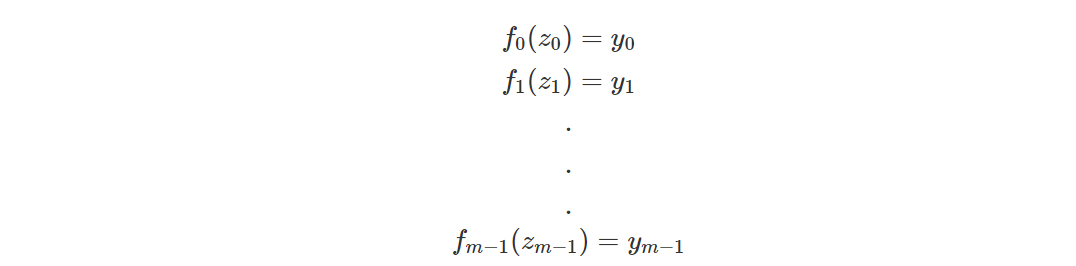Согласно предыдущему описанию (KZG для одной точки), для каждого полинома существует частный полином, удовлетворяющий:
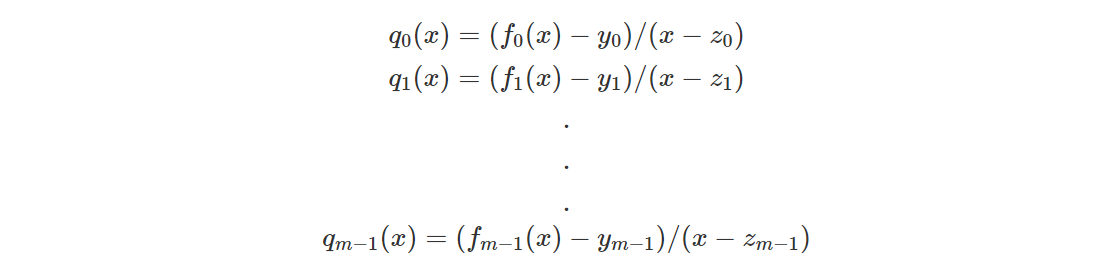Прувер должен выполнить обязательство исходного полинома и частного полинома и отправить его верификатору :

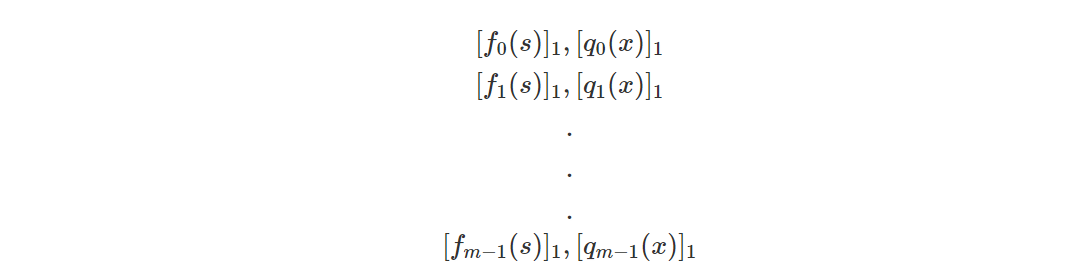
Верификатор выполняет проверку:
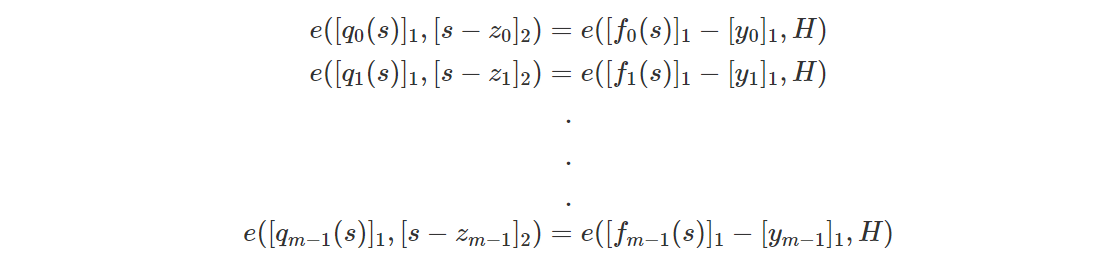Очевидно, что мы не хотим, чтобы верификатор выполнял так много операций сопряжения (это дорого) . Поэтому нам нужно выполнить Compress следующим образом.

Сгенерируйте несколько случайных чисел r_0,r_1,....,r_m−1 и соберите приведенные выше частные полиномы вместе:
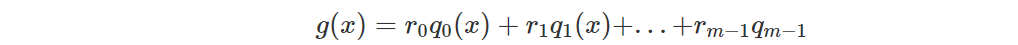Предположим, что тогда и только тогда, когда каждый q_i(x) является полиномом, g(x) будет полиномом (вероятность того, что дроби между q_i(x) точно смещены, очень мала из-за случайных чисел ).

Доказывающая сторона принимает полином g(x) и отправляет [g(s)]_1 проверяющей стороне.

Затем пусть верификатор считает, что [g(s)]_1 является приверженностью полиному g(x).

Обратите внимание на форму полинома g(x)g(x), который можно записать как:

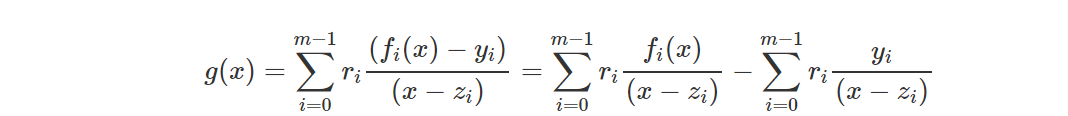
Выберите значение tt случайным образом, и вы получите:

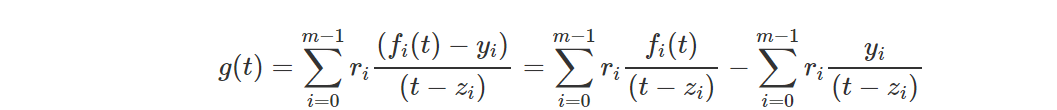
Определите полином:

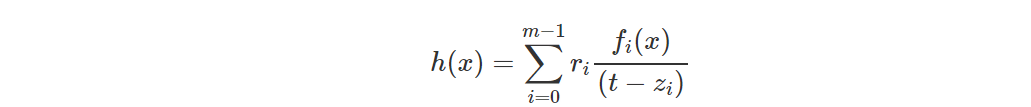
Его обязательства можно рассчитать следующим методом:

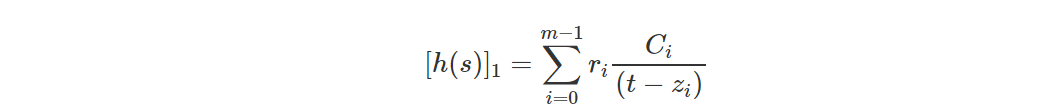
Тогда значение полинома h(x)−g(x)h(x)−g(x) в точке tt равно:

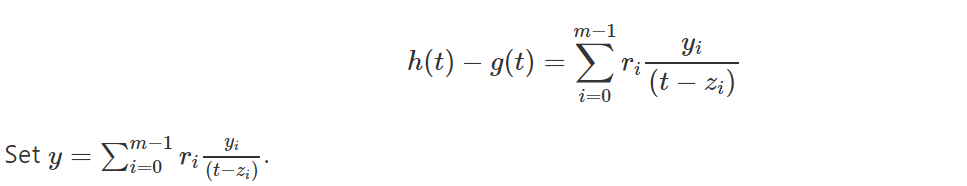
Вычислите фактор-полином q(x)=(h(x)−g(x)−y)/(x−z).

Рассчитайте обязательство π = [q(s)]_1=[(h(s)−g(s)−y)/(s−t)]_1, и отправьте его верификатору.

Verifier выполняет следующую проверку:

1. Рассчитать

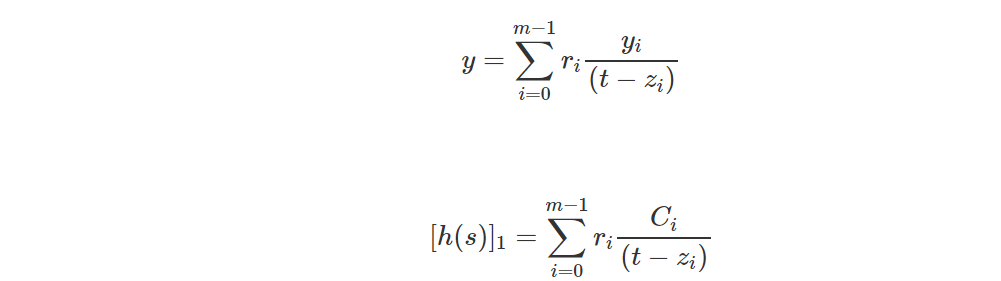
1. Подтвердить

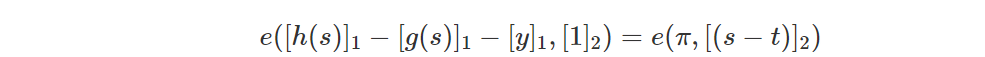
Ключевые свойства

1. По этой схеме можно доказать любое количество точек без изменения размера доказательства. (Для каждого обязательства есть доказательство π.)

1. Значение y_i не нужно указывать явно, так как это хэш значения следующего слоя.

1. Значение x_i не нужно указывать явно, так как его можно определить по ключу.

1. Используемая общедоступная информация включает в себя пару ключ/значение, подлежащую проверке, и соответствующие обязательства от базового уровня до верхнего уровня.

Рекомендации

1. Данкрад Файст, «Мультидоказательства PCS с использованием случайной оценки», https://dankradfeist.de/ethereum/2021/06/18/pcs-multiproofs.html, дата обращения: 10 мая 2022 г.

1. Виталик Бутерин, «Деревья Веркле», https://vitalik.ca/general/2021/06/18/verkle.html, дата обращения: 10 мая 2022 г.

1. Джон Кусмаул, «Деревья Веркле», https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf, дата обращения: 10 мая 2022 г.