Последовательный исчисление против CPS: перспектива компилятора на потребителей и стратегии оценки
9 июля 2025 г.Таблица ссылок
Введение
Перевод на последовательное исчисление
2.1 Арифметические выражения
2.2 Пусть привязки
2.3 Определения верхнего уровня
2.4 Алгебраические данные и типы кодов
2.5 первоклассные функции
2.6 Операторы управления
Оценка в контексте
3.1 Контексты оценки для развлечения
3.2 Сосредоточение внимания на оценке в сердечнике
Правила печати
4.1 Правила печати для развлечения
4.2 Правила печати для Core
4.3 Тип. Звукость
Понимание
5.1 Контексты оценки являются первым классом
5.2 Данные двойные до кодата
5.3 LET-связы
5.4 Трансформация случая
5.5 Прямой и косвенный потребители
5.6 Позвоните в запас, вызовов и eta-laws
5.7 Линейная логика и двойственность исключений
Связанная работа
Заключение, заявление о доступности данных и подтверждение
A. Взаимосвязь с последовательным исчислением
B. Правила набора развлечений
C. Оперативная семантика лейбла/goto
Ссылки
5.5 Прямой и косвенный потребители
Как упоминалось во введении, естественным конкурентом последовательного исчисления в качестве промежуточного представления является стиль продолжения передачи (CPS). В CPS контексты оценки Reive представлены функциями. Это делает полученные типы программ в CPS, возможно, труднее понять. Однако существует еще одно преимущество последовательного исчисления по сравнению с CPS, как описано Downen et al. [2016]. Первоклассное представление потребителей в последовательном исчислении позволяет нам различать два различных вида потребителей: прямые потребители, то есть деструкторы и косвенные потребители. В частности, это позволяет цепорить прямых потребителей так же, как и в веселье.
Предположим, что у нас есть тип кода с деструкторами Get и устанавливается для получения и установки значения ссылки. Теперь рассмотрим следующую цепочку Destructor Calls на ссылку 𝑟 В веселье
𝑟 .set (3) .set (4) .get ()
Компилятор мог бы использовать пользовательское правило переписать пользовательское правило для переписывания двух последующих вызовов, чтобы установить только второй вызов. В ядре приведенный выше пример выглядит следующим образом:
𝜇𝛼.⟨𝑟 | set (3; set (4; get (𝛼)⟩
Мы по -прежнему можем сразу же увидеть прямую цепочку деструкторов и, таким образом, применять по существу одно и то же правило переписывания. В CPS, однако, пример скорее станет
𝜆𝑘. 𝑟 .set (3; 𝜆𝑠. 𝑠.set (4; 𝜆𝑡. 𝑡 .get (𝑘))))
Цепочка деструкторов становится запутанной за счет оборотов, введенных путем представления продолжения для каждого деструктора в качестве функции. Чтобы применить пользовательское правило переписывания, упомянутое выше, необходимо увидеть через Lambdas, то есть правило пользовательского переписывания должно быть преобразовано, чтобы быть применимым.
5.6 Позвоните в запас, вызовов и eta-laws
В разделе 2.2 мы уже указали на существование утверждений ⟨𝜇𝛼.𝑠1 | 𝜇𝑥.𝑠 ˜ 2⟩, которые называются критическими парами, потому что они могут быть априори, чтобы быть уменьшенным до 1 [𝜇𝑥.𝑠 ˜ 2/𝛼] или2 [𝜇𝛼.𝑠1/𝑥]. Эти критические пары уже обсуждались Куриен и Хербелин [2000], когда они представили 𝜆𝜇𝜇 𝜆𝜇𝜇-calculus. Одним из решений является выбрать порядок оценки, либо по вызову (CBV), либо по вызову (CBN), который определяет, к какому из двух утверждений мы должны оценить, и в этой статье мы решили всегда использовать порядок оценки по вызову. Разница между этими двумя вариантами также обсуждалась Wadler [2003]. Обратите внимание, что эта свобода для стратегии оценки является еще одним преимуществом последовательного исчисления по сравнению с стилем продолжения, поскольку последний всегда исправляет стратегию оценки.
Какой порядок оценки, который мы выбираем, имеет важное следствие для оптимизации, которые мы можем выполнять в компиляторе. Если мы выбираем вызов по цене, то нам не разрешается использовать все 𝜂-равенства для типов кодат, и если мы используем вызов, то нам не разрешено использовать все 𝜂-равновесие для типов данных. Давайте проиллюстрируем проблему в случае типов кодат со следующим примером:
⟨Cocase {ap (𝑥; 𝛼) ⇒ ⟨𝜇𝛽.𝑠1 | AP (𝑥; 𝛼)⟩} | 𝜇𝑥.𝑠 ˜ 2⟩ ≡𝜂 ⟨𝜇𝛽.𝑠1 | 𝜇𝑥.𝑠 ˜ 2⟩
Мы предполагаем, что 𝑥 и 𝛼 не выглядят свободными в 𝑠1. 𝜂-трансформация-это просто обычный 𝜂-закост для функций, но применяется к представлению функций как типов кодат. Заявление с левой стороны уменьшает 𝜇 𝜇 𝜇 сначала как по вызову, так и в порядке оценки по вызову, т.е.
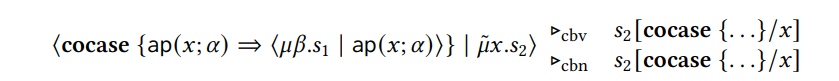
Правая сторона 𝜂 equality, однако, снижает 𝜇 сначала под приказом оценки по вызову, т.е.
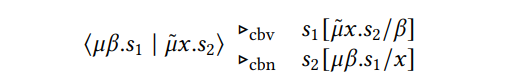
Следовательно, 𝜂 equality действует только в соответствии с порядок оценки по вызову. Этот пример показывает, что достоверность применения этого 𝜂-правила в качестве оптимизации зависит от того, использует ли язык по вызову или вызову. Если бы вместо этого мы использовали тип данных, такой как пара, аналогичная 𝜂-уменьшением даст только тот же результат, что и исходный оператор при использовании вызовов.
5.7 Линейная логика и двойственность исключений
Мы представили пару типов данных (𝜎, 𝜏) и LPAIR типа Codata (𝜎, 𝜏) в виде двух разных способов формализации кортежей. Пара типов данных (𝜎, 𝜏) определяется конструктором, аргументы которого с нетерпением оцениваются, поэтому этот тип соответствует строгим кортежам на таких языках, как ML или OCAML. LPair Type Codata (𝜎, 𝜏) - это ленивая пара, которая определяется двумя проекциями FST и SND, и только тогда, когда мы вызовыте первую или вторую проекцию, мы начинаем вычислять его содержимое. Это ближе к тому, как ведут ведущие кортежи на ленивом языке, как Хаскелл.
Линейная логика [Girard 1987; Wadler 1990] добавляет еще одну разницу в эти типы. В линейной логике мы рассматриваем аргументы как ресурсы, которые не могут быть произвольно дублироваться или отброшены; Каждый аргумент для функции должен использоваться ровно один раз. Если мы следуем этой более строгой дисциплине, то мы должны различать два разных типа пар: для использования пары 𝜎 𝜏 𝜏 (произносится «время» или «тензор»), мы должны использовать как 𝜎, так и 𝜏, но если мы хотим использовать пару 𝜎 & 𝜏 (произносится «с»), мы должны выбрать либо, чтобы использовать 𝜎 или 𝜏. Теперь легко увидеть, что тип 𝜎 𝜏 𝜏 из линейной логики соответствует паре типа данных (𝜎, 𝜏), поскольку, когда мы соответствуем шаблону по этому типу, мы получаем две переменные в контексте, одна для 𝜎 и один для 𝜏. Тип 𝜎 & 𝜏 аналогично соответствует типу LPAIR (𝜎, 𝜏), который мы используем, вызывая либо первую, либо вторую проекцию, потребляя всю пару.


Авторы:
(1) Дэвид Биндер, Университет Тюбингена, Германия;
(2) Марко Цшенке, Университет Тюбингена, Германия;
(3) Мариус Мюллер, Университет Тюбингена, Германия;
(4) Клаус Остерманн, Университет Тюбингена, Германия.
Эта статья есть
Оригинал

