
Возвращаясь к противоречиям в теории диффузии: решение проблемы Милна для B-частиц
4 сентября 2024 г.Автор:
(1) К. Рази Накви, физический факультет, Норвежский университет науки и технологий (NTNU), 7094 Тронхейм, Норвегия
Таблица ссылок
Аннотация и 1 Введение
2 Предварительный материал
3 комментария, вызванные решением проблемы Милна для B-частиц
4 Поток в сферическую ловушку
5 Молекулярное движение в жидкостях
6 Заключительные замечания и ссылки
3 комментария, вызванные решением проблемы Милна для B-частиц

Вдали от стенки плотность линейно увеличивается с расстоянием, как и следует из уравнения диффузии. Когда это асимптотическое решение экстраполируется через граничную область, оно достигает нуля не на стенке (как это было бы в случае решения уравнения диффузии с поглощающей границей), а на некотором расстоянии за ней. Значение, которое мы находим для этой «длины экстраполяции Милна», в соответствующих безразмерных единицах примерно вдвое больше значения, найденного в задаче переноса излучения. Плотность в реальном решении везде ниже, чем у экстраполированного асимптотического решения, но, конечно, она остается конечной на стенке.

3.1 Масштабы длины для броуновского движения и его обратных

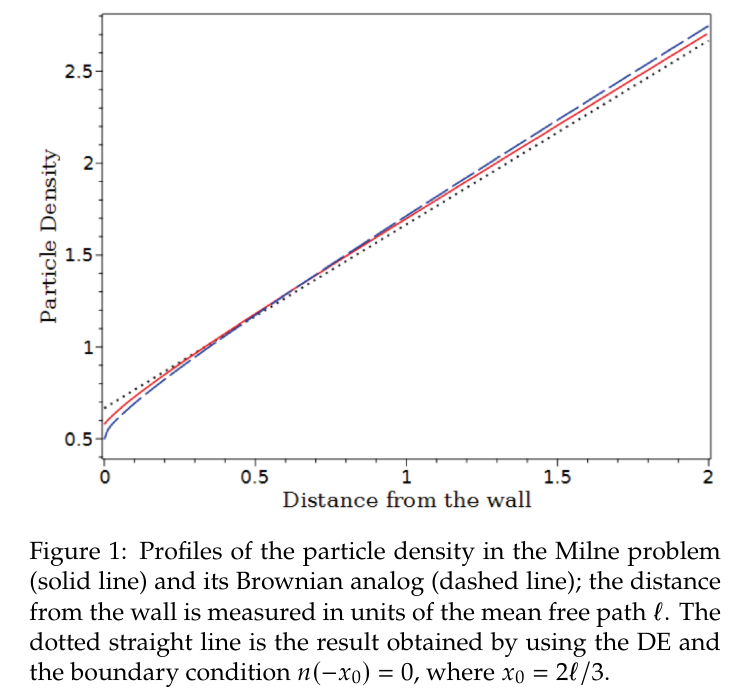
3.2 Профили плотности частиц

Эта статьядоступно на arxivпо лицензии CC BY 4.0 DEED.
Оригинал

