Возвращаясь к противоречиям в теории диффузии: поток в сферическую ловушку
tech-stories diffusion-theory milne-problem smoluchowski-equation brownian-motion radiative-transfer kinetic-boundary-layer bimolecular-reactions theoretical-physics

Возвращаясь к противоречиям в теории диффузии: поток в сферическую ловушку

4 сентября 2024 г.

Автор:

(1) К. Рази Накви, физический факультет, Норвежский университет науки и технологий (NTNU), 7094 Тронхейм, Норвегия

Аннотация и 1 Введение

2 Предварительный материал

3 комментария, вызванные решением проблемы Милна для B-частиц

4 Поток в сферическую ловушку

5 Молекулярное движение в жидкостях

6 Заключительные замечания и ссылки

4 Поток в сферическую ловушку

Для поглощения R-частиц сферической ловушкой радиуса 𝑅 Зифф нашел «длину экстраполяции Милна», равную ≈ 0,29795219𝑙 для 0 < 𝑙 ≤ 2𝑅. Поскольку этот результат противоречит (по крайней мере на первый взгляд) большому количеству работ по тесно связанным проблемам, включая некоторые работы, выполненные настоящим автором, и никакого решения не было предложено в статье Зиффа [20] или в двух ее блестящих продолжениях [21, 22], исследование несоответствия оправдано.

Таким образом, мы приходим к, казалось бы, безвкусному, но возвышенно примирительному выводу, что выражения

4.1 Граничное условие на стенке

4.2 Граничное условие для сферического стока

Ссылаясь на четыре статьи Коллинза и его коллег, Зифф делает два замечания, заявляя, во-первых, что «константа 𝛾 [линейная длина экстраполяции] должна определяться эмпирическими аргументами», а во-вторых, что «в низшем порядке они [имея в виду различные предписания Коллинза и др.] обычно дают один и тот же результат 𝛾 = (𝑙/3)[1 + 𝒪(𝜀)], . . », где 𝜀 ≡ 𝑙/𝑅. Я не вижу однозначного утверждения на этот счет ни в одной из четырех статей, цитируемых Зиффом (его ссылки 15–18). В своих уравнениях (3) и (4), воспроизведенных здесь в моих обозначениях, Фриш и Коллинз [23] дают наиболее четкое изложение своего BC:

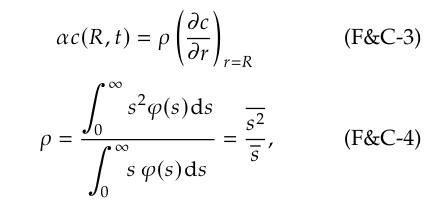
Поскольку зависимость 𝛼 неверна (см. ниже), а нас интересует черная сфера, мы установим 𝛼 = 1 в уравнении (F&C-3). Изучая ссылку 15 статьи Ziff 1949 года [24], можно убедиться, что уравнение (F&C-4) следует изменить на

но общее утверждение о 𝜌 (которое должно быть отождествлено с линейной длиной экстраполяции для черной сферы) все еще недостижимо, поскольку «скачки», обсуждавшиеся выше, можно по существу рассматривать как путь молекулы между последовательными столкновениями. Однако сохранение скорости при столкновении приводит к тому, что функция плотности скачков 𝜑(𝑠) больше не является сферически однородной, а зависит от направления скачка, непосредственно предшествующего рассматриваемому скачку, в манере марковского процесса. Однако, . . . этот эффект можно учесть, умножив ⟨𝑠 2 ⟩ на поправочный коэффициент, немного больший единицы. Для удобства в этом обсуждении будет предполагаться, что этот поправочный коэффициент уже включен в ⟨𝑠 2 ⟩ и в другие моменты 𝜑(𝑠).

Для двух интересующих нас случаев, а именно L-частиц и R-частиц, мы получаем 𝜌 = 2ℓ/3 и 𝜌 = 𝑙/3, что согласуется с расчетами, основанными на плоской симметричной системе.

Здесь стоит добавить, что можно показать, что модель скачка, представленная в цитированной выше статье 1949 года [24], подразумевает следующее граничное условие для серой сферы:

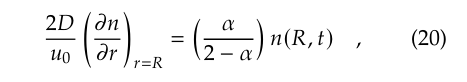
Однако этот вывод не был опубликован до 1982 года [7].

4.3 Случай малой сферы: ахиллесова пята «случайного блуждания Пирсона-Рэли»

До сих пор мы не столкнулись ни с одним выводом (вытекающим из модели Зиффа), который нельзя было бы примирить с его аналогами из обратного и регулярного броуновского движения. Однако расчеты Зиффа показали, что длина экстраполяции 𝛾 не зависит от 𝑙/𝑅 при 0 < 𝑙/𝑅 ≤ 2, что резко контрастирует с результатами, полученными в исследованиях переноса нейтронов, которые были обобщены Сахни [25] и Уильямсом [26], оба из которых также представили свои собственные расчеты. Когда был исследован броуновский аналог этой проблемы, константа скорости коагуляции показала неоднозначную зависимость от значения Λ/𝑅 [27–29]; важный вывод, вытекающий из этих исследований, стоит подчеркнуть еще раз: когда для решения KKE используются методы моментов, попытки получить лучшие результаты путем увеличения числа моментов окажутся тщетными, потому что за пределами определенного порядка сходимость теряется.

Эта статьядоступно на arxivпо лицензии CC BY 4.0 DEED.

Оригинал

Recent Post

Categories

PREVIOUS ARTICLE
NEXT ARTICLE