
Возвращаясь к противоречиям в теории диффузии: заключительные замечания и ссылки
4 сентября 2024 г.Автор:
(1) К. Рази Накви, физический факультет, Норвежский университет науки и технологий (NTNU), 7094 Тронхейм, Норвегия
Таблица ссылок
Аннотация и 1 Введение
2 Предварительный материал
3 комментария, вызванные решением проблемы Милна для B-частиц
4 Поток в сферическую ловушку
5 Молекулярное движение в жидкостях
6 Заключительные замечания и ссылки
6 Заключительные замечания

Утверждение, мотивированное поиском лучшего граничного условия, что модель Лоренца является полезным инструментом для исследования бимолекулярных реакций в растворах, стало достоверным только после публикации численного решения одномерного KKE Буршки и Тайтулера [4]. Непосредственно перед этим один критик выразил «мнение сообщества», заявив в рецензируемом отчете (по статье, написанной в соавторстве со мной), что LBE «абсолютно бесполезна при рассмотрении переноса в жидкостях», и настаивал на том, что эта задача лучше всего решается путем решения KKE. Только тогда возникла необходимость в сравнении масштабов длины обратного и регулярного броуновского движения. Группа из Тронхейма показала, что обратное броуновское движение, регулярное броуновское движение и модель BGK неразличимы на уровне DE, при условии использования соответствующего BC [31], а именно того, который указан в уравнении (20). Прокрустова модель случайного блуждания, не допускающая распределения длин путей, кажется (мне) нефизической, во многом подобно решеточной модели, которая легла в основу размышлений Смолуховского (о граничном условии на поглощающей поверхности) и ввела в заблуждение целые поколения студентов, а также поклонников химической кинетики.
Бесконечно тяжелые B-частицы, бесконечно легкие L-частицы, бесконечно негибкие (в отношении постоянства их траекторий) R-частицы — все это выдумки, но некоторые выдумки более плодотворны, чем другие, а некоторые просто бесполезны. Принесет ли выдумка R-частиц плоды (в условиях диффузионно-опосредованных реакций) или послужит лишь отвлечением, еще предстоит выяснить.
Задача Милна: расчет профилей плотности
Целью данного приложения является предоставление возможности читателю данной статьи сгенерировать данные, используемые для построения профилей плотности, показанных на рис. 1.
Данные о плотности для L-частиц были получены с помощью вариационного расчета [32], в котором ℓ использовалась как единица длины. Соответствующие данные для B-частиц были вычислены путем улучшения результатов, полученных группой из Тронхейма, с помощью обработки в полудиапазоне [10], в которой приближение 𝑁-го порядка для плотности частиц 𝑛 было выражено в виде
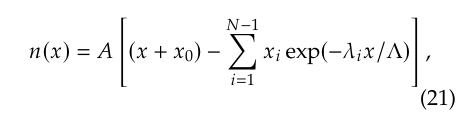
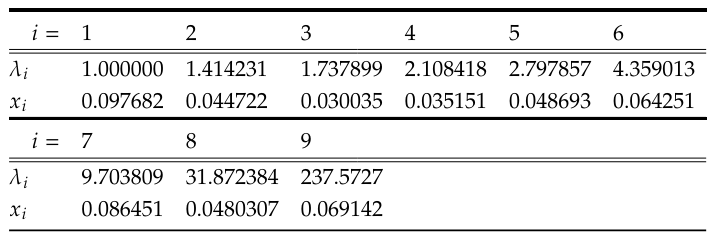
и значения 𝑥0 (1,459877Λ), 𝑥𝑖 и 𝜆𝑖 (для 𝑖 =1–8), полученные в результате приближения девятого порядка (𝑁 = 8), были представлены, а значения 𝑛(𝑥) вблизи стенки были сравнены со значениями, найденными Маршаллом и Уотсоном (M&W) на основе их точной аналитической обработки [33]. Улучшения состоят из трех незначительных изменений: значение 𝑥0 было заменено на 𝑥0 = 1,460354Λ (первые семь цифр точного результата), был добавлен еще один член, а значения 𝑥𝑖 и 𝜆𝑖 для последних трех членов (𝑖 =7–9) были оптимизированы методом наименьших квадратов для чисел в столбце (A) Таблицы 1 M&W. Полный набор значений {𝑥𝑖 , 𝜆𝑖} (в основном аналитического, частично эмпирического происхождения) отображен в Таблице 1, верхняя часть которой идентична Таблице II из [10]. Для построения графика плотности B-частиц на Рис. 1 шкала длины была изменена с Λ на ℓ.
Ссылки
[1] М. фон Смолуховский. Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen. Физик. Zeit., 17:568–571 (1-я часть), 585–593 (2-я часть), 1916.
[2] М. фон Смолуховский. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. З. Физ. хим. (Лейпциг), 92: 129–168, 1917.
[3] М. фон Смолуховский. Grundriß der Koagulationskinetik kolloider Lösungen. Коллоид З., 21:98–104, 1917.
[4] М. А. Буршка и У. М. Титулаер. Кинетический пограничный слой для уравнения Фоккера-Планка с поглощающей границей. J. Stat. Phys., 25:569–582, 1981.
[5] К. Рази Накви, К. Дж. Морк и С. Вальденстрём. Комментарий к «Устойчивому одномерному броуновскому движению с поглощающей границей». J. Chem. Phys., 77(7):4263–4264, 1982.
[6] К. Рази Накви, К. Дж. Морк и С. Вальденстрём. Редукция уравнения Фоккера-Планка с поглощающей или отражающей границей к уравнению диффузии и граничному условию излучения. Phys. Rev. Lett., 49:304–307, 1982.
[7] К. Рази Накви, С. Вальденстрём и К. Дж. Морк. Кинетика диффузионно-опосредованных бимолекулярных реакций. Новая теоретическая основа. J. Phys. Chem., 86:4750–4756, 1982.
[8] К. Рази Накви, С. Вальденстрём и К. Дж. Морк. О скорости поглощения броуновских частиц чёрной сферой: связь между уравнением Фоккера–Планка и уравнением диффузии. J. Chem. Phys., 78(5):2710–2712, 1983.
[9] Энрико Ферми (автор) и Эмилио Сегре (главный редактор). Сборник статей (Note E Memorie), (т. 1: Италия, 1921–1938). Издательство Чикагского университета, Чикаго, Иллинойс, 1962.
[10] К. Рази Накви, К. Дж. Морк и С. Вальденстрём. Стационарное одномерное уравнение Фоккера-Планка с поглощающей границей: полудиапазонная обработка. Phys. Rev. A, 40:3405–3407, 1989.
[11] С. Вальденстрём, К. Дж. Морк и К. Рази Накви. Задача Милна для твердосферного газа Рэлея: исследование на основе уравнения Фоккера-Планка. Phys. Rev. A, 28(3):1659–1661, 1983.
[12] С. В. Г. Менон, Винод Кумар и Д. К. Сахни. Подход функции Грина к решению зависящего от времени уравнения Фоккера-Планка с поглощающей границей. Physica A: Statistical Mechanics and its Applications, 135(1):63–79, 1986.
[13] М. Дж. Линденфельд и Б. Шизгал. Проблема Милна: исследование зависимости массы. Phys. Rev. A, 27:1657–1670, 1983.
[14] Кнуд Андерсен и Курт Э. Шулер. О релаксации твердосферного газа Рэлея и Лоренца. J. Chem. Phys., 40(3):633–650, 1964.
[15] Б. Дэвисон, Теория переноса нейтронов, Оксфорд, 1957.
[16] Джулиан Кейлсон и Джеймс Э. Сторер. О броуновском движении, уравнении Больцмана и уравнении Фоккера-Планка. Quarterly of Applied Mathematics, 10(3):243–253, 1952.
[17] М. Р. Хоар. Линейный газ. В книге Ильи Пригожина и Стюарта А. Райса, редакторов, Advance in Chemical Physics, том 20, страницы 135–214. Wiley-Interscience, Нью-Йорк, 1971.
[18] Мария Смолуховская. Sur le chemin moyen parcouru par les molecules d’un gas et sur son rapport avec la theorie de la диффузии. Бык. акад. наук. Краковье, страницы 202–213, 1906 г.
[19] К. Рази Накви. Более 100 лет колоссальной путаницы в коллоидной коагуляции. Часть I: Работа Смолуховского о поглощающих границах. arXiv:2404.17021 [cond-mat.stat-mech], страницы 1–20, 2024.
[20] Роберт М. Зифф. Поток в ловушку. J. Stat. Phys., 65(5):1217–1233, 1991.
[21] С. Н. Маджумдар, А. Конте и Р. М. Зифф. Единое решение ожидаемого максимума случайного блуждания в дискретном времени и дискретного потока в сферическую ловушку. J. Stat. Phys., 122(5):833–856, 2006.
[22] Р. М. Зифф, С. Н. Маджумдар и А. Конте. Общий поток в ловушку в одном и трех измерениях. J. Phys.: Condens. Matter, 19(6):065102, 2007.
[23] Х. Л. Фриш и Ф. К. Коллинз Диффузионные процессы в росте аэрозольных частиц. J. Chem. Phys., 20:1797–1803, 1952.
[24] Ф. К. Коллинз и Г. Э. Кимбалл, «Реакции, контролируемые диффузией в жидких растворах», Ind. Eng. Chem., 41(11):2551–2553, 1949.
[25] Д. К. Сахни. Влияние черной сферы на распределение потока в бесконечном замедлителе. J. Nucl. Energy, 20(11):915–920, 1966.
[26] М. М. Р. Уильямс. Простой метод расчета линейного расстояния экстраполяции на поверхности черного тела. Annals of Nuclear Energy, 15(2):101–105, 1988.
[27] Винод Кумар и С. В. Г. Менон. Скорость конденсации на черной сфере с помощью уравнения Фоккера-Планка. J. Chem. Phys., 82(2):917–920, 1985.
[28] М. Э. Виддер и У. М. Титулаер. Кинетический пограничный слой вокруг поглощающей сферы и рост мелких капель. J. Stat. Phys., 55(5/6):1109–1127, 1989.
[29] С. Вальденстрём и К. Рази Накви. Стационарная скорость поглощения (серой сферой) частиц, подчиняющихся уравнению Фоккера-Планка: анализ результатов, полученных моментными методами. Ark. Fys. Seminar Trondheim, (4):1–37, 1988.
[30] Джоэл Х. Хильдебранд. Движение молекул в жидкостях: вязкость и диффузия. Science, 174(4008):490–493, 1971.
[31] К. Рази Накви, К. Дж. Морк и С. Вальденстрём. Уравнения переноса и граничные условия для описания движения в однородном растворителе с полностью поглощающей границей. Ark. Fys. Seminar Trondheim, (7):1–36, 1982.
[32] К. Рази Накви. Задача Милна для незахватывающей среды: точные аналитические приближения для плотности частиц и возникающее угловое распределение. J. Quant. Spectrosc. Radiat. Transfer, 50(1):59–64, 1993.
[33] Т. В. Маршалл и Э. Дж. Уотсон. Аналитические решения некоторых задач пограничного слоя в теории броуновского движения. J. Phys. A: Math. Gen., 20(6):1345–1354, 1987.
Эта статьядоступно на arxivпо лицензии CC BY 4.0 DEED.
Оригинал

