
QLoRA: точная настройка LLM с помощью одного графического процессора
3 января 2024 г.В моей предыдущей статье мы видели о Low -Адаптация ранга или LoRA. LoRA весьма эффективен для развертывания больших моделей, а также быстр для вывода, тем самым решая проблему вывода точно настроенных LLM. Однако когда дело доходит до тренировок, LoRA не помогает. Например, для точной настройки модели LLAMA с 65 миллиардами параметров LoRA требуется 780 ГБ памяти графического процессора. Это около 16 графических процессоров A40. Ответ на эту проблему лежит в QLoRA, где Q означает квантование. Основная мотивация QLoRA — добиться тонкой настройки на одном графическом процессоре.
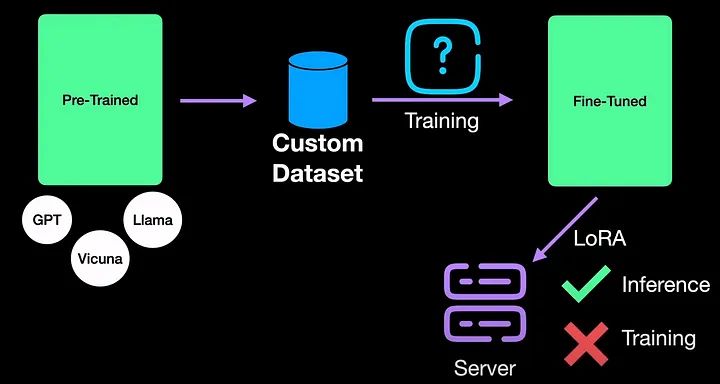
QLoRA делает это с помощью всего трех нововведений, а именно: 1. 4-битный NormalFloat (NF4), новый тип данных, который теоретически оптимален для нормально распределенных весов. 2. Двойное квантование для уменьшения среднего объема памяти за счет квантования констант квантования. 3. Оптимизаторы страниц для управления скачками памяти.
В этой статье давайте рассмотрим все три новинки и разберемся в QLoRA.
Визуальное обучение
Если вы, как и я, хорошо обучаетесь визуальному зрению, и вам нужна видеоверсия этой статьи, вы можете найти ее на YouTube:
https://youtu.be/6l8GZDPbFn8?si=Dx7ubp9bLpb-_lTP&embedable=true
Квантование
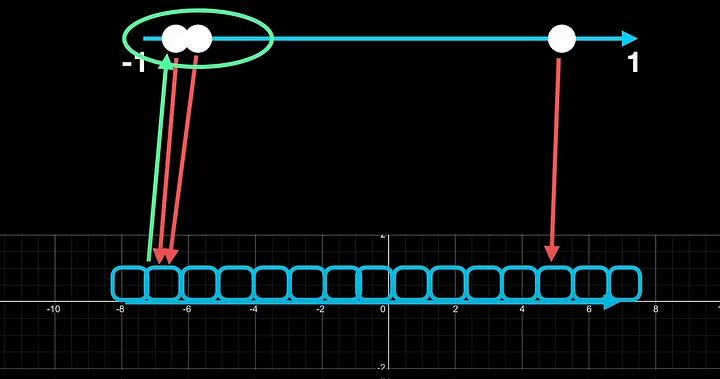
Начнем с квантования, которое является фундаментальным для QLoRA. Проще говоря, квантование работает путем округления и усечения для упрощения входных значений.
Для простоты предположим, что мы квантоваем от Float16 до int4. Int4 имеет диапазон от -8 до 7. Поскольку у нас есть только 4 бита для работы, мы можем иметь только 2 степени 4, что составляет 16 ячеек для квантования. Таким образом, любое входное значение с плавающей точкой должно быть сопоставлено с центрами одного из этих 16 интервалов.
В нейронных сетях входными данными являются тензоры, представляющие собой большие матрицы. И они обычно нормализуются между -1 и 1 или 0 и 1. Давайте рассмотрим случай простого тензора с тремя значениями, скажем, -0,976, 0,187 и 0,886. Нам повезло с этим примером, поскольку значения равномерно распределены по нормализованному диапазону. Когда мы квантоваем до int4, каждое из трех чисел занимает уникальный интервал.
Одной из проблем с квантованием являются выбросы, что побуждает к блочному квантованию.
Давайте возьмем немного другой пример, где входные значения больше не равномерно распределены во входном диапазоне. Пусть два входа расположены близко друг к другу, а один далеко друг от друга. Если мы теперь квантоваем до int4, первые два числа попадут в один и тот же интервал. а с третьим все в порядке. О, нам это не нужно, потому что, если вы вообще захотите деквантовать и преобразовать обратно в число с плавающей запятой16, эти два числа больше не преобразуются обратно в уникальные значения. Другими словами, мы потеряли ценную информацию из-за ошибки квантования.
Блоковое квантование
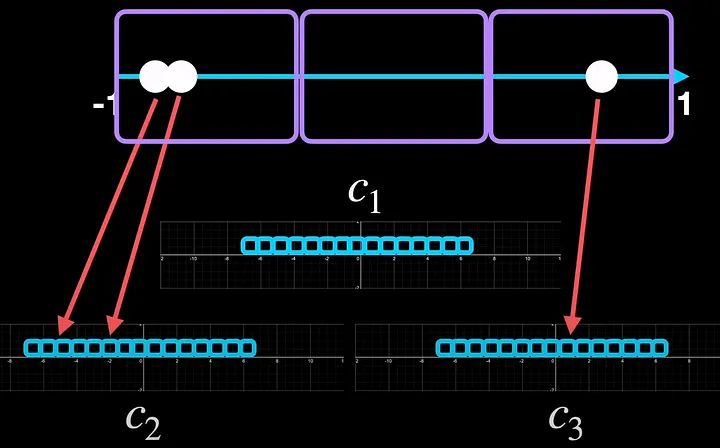
Блочное квантование, при котором мы делим входной диапазон на блоки. На иллюстрации показаны три блока, каждый из которых имеет свои константы квантования.
Одним из способов решения этой проблемы может быть разделение входного диапазона на отдельные блоки. В этом примере у нас есть три блока. И мы квантуем каждый блок отдельно, каждый из которых имеет свой диапазон. Итак, теперь два значения, которые расположены близко друг к другу, находят разные ячейки внутри блока. А с третьим проблем не было, так что все в порядке.
Разделив на блоки, мы независимо квантовали каждый блок, и поэтому каждый блок имеет свои параметры квантования, которыми часто является константа квантования c. В этом примере это c_1, c_2 и c_3.
То, что мы только что видели, — это поблочное квантование, которое мы проиллюстрировали тремя блоками
.Но на практике QLoRA использует размер блока 64 для весов для высокой точности квантования.
Обычный плавающий
Говоря о весах, одно из интересных свойств предварительно обученных весов нейронной сети заключается в том, что они нормально распределены и сосредоточены вокруг нуля.
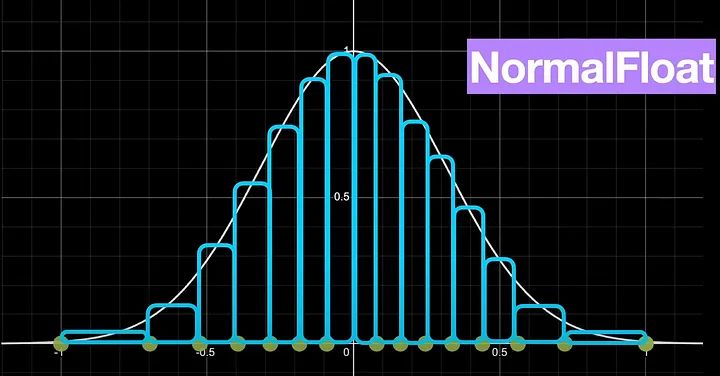
Повторное взвешивание значений квантования с нормальным распределением приводит к типу данных NormalFloat
Это означает, что существует очень высокая вероятность появления значений ближе к нулю, а не к -1 или плюс 1. Но наше стандартное квантование до int4 не учитывает этот факт. При этом предполагается, что каждая из 16 ячеек имеет равную вероятность получения значений.
Чтобы решить эту проблему с помощью стандартного квантования, мы можем разработать немного специализированный тип квантования, который учитывает нормальное распределение весов нейронной сети. Именно это и делает QLoRA, называя его k-bit NormalFloat. В NormalFloat бины взвешиваются по нормальному распределению, и, следовательно, расстояние между двумя значениями квантования далеко друг от друга вблизи крайних значений -1 или 1, но становится ближе друг к другу по мере приближения к 0.
Чтобы пролить дополнительный свет, зеленые точки показывают 4-битное квантование NormalFloat по сравнению со стандартным 4-битным квантованием, показанным синими точками.
Теперь перейдем к следующему разделу статьи — двойному квантованию.
Поскольку целью QLoRA является обучение на одном графическом процессоре, важно максимально использовать каждый бит памяти. Если мы вспомним блочное квантование, то увидим, что для квантования весов мы используем 64 блока, и каждый из этих блоков имеет константу квантования *c*. Итак, двойное квантование — это процесс квантования констант квантования для дополнительной экономии памяти. А за счет двойного квантования мы получаем в среднем полбита на каждый параметр.
Последний кусочек головоломки — оптимизаторы страничного поиска.
Оптимизаторы страниц

Страничные оптимизаторы используют память ЦП всякий раз, когда происходит переполнение памяти графического процессора, тем самым справляясь с длинными последовательностями.
Страничные оптимизаторы предотвращают скачки памяти всякий раз, когда мы внезапно получаем длинный ввод. Допустим, мы работаем с документами, и вдруг у нас появился длинный документ. Когда мы используем для обучения один графический процессор, такой скачок длины последовательности обычно нарушает обучение. Чтобы преодолеть эту проблему, состояние оптимизатора, скажем, Адама, перемещается из памяти графического процессора в процессор до тех пор, пока не будет прочитана длинная последовательность. Затем, когда память графического процессора освобождается, оптимизированное состояние возвращается обратно в графический процессор. На высоком уровне именно это произойдет, если мы задействуем оптимизаторы страничного просмотра.
С точки зрения реализации страничный оптимизатор является частью библиотеки битов и байтов. И вы можете включить или отключить его во время обучения QLoRA, просто установив или выключив флаг is_paged.
Объединяя три вышеупомянутых компонента, QLoRA эффективно использует тип данных хранения низкой точности, в нашем случае обычно 4-битный, и один тип вычислительных данных, обычно BFloat16.
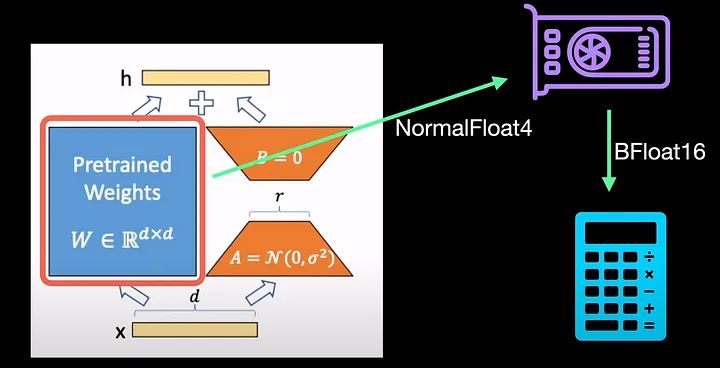
Что это значит? Возвращаясь к LoRA, это означает, что для оптимизации памяти веса модели сохраняются в NF4. Это позволяет нам загружать веса в один графический процессор, а загруженные веса преобразуются в BFloat16 для вычисления градиентов во время обратного распространения ошибки.
Чтобы связать его с LoRA, давайте вернемся к этому уравнению из LoRA, где x — это входные данные, а W_0 — это веса нашей предварительно обученной модели. A и B — разложение матрицы низкого ранга.

В случае с QLoRA мы вводим x — BrainFloat16. Наши веса хранятся как Normal Float4 (NF4). Во время вычисления градиентов наши веса и константы квантования проходят двойное деквантование, которое является обратным двойному квантованию. Это происходит путем предварительного деквантования констант квантования c_1 и c_2. Затем, используя константы, мы еще раз деквантуем веса в BrainFloat16, который используется для вычисления градиентов.
Если вам интересно, насколько хороши NormalFloat и двойное квантование, авторы QLoRA экспериментировали с четырьмя наборами данных и показали, что во всех четырех случаях использование нормального плавающего числа и двойного квантования повышает среднюю точность обучения с нулевым шагом по сравнению с простым использованием плавающего числа.< /п>
Что касается оценки GLUE, QLoRA может повторять точность 16-битного LoRA и полной точной настройки. Авторы приходят к выводу, что 4-битная QLORA с типом данных NF4 соответствует производительности 16-битной полной точной настройки и 16-битной точной настройки LoRA в академических тестах с хорошо зарекомендовавшими себя настройками оценки.
Итак, если вы заинтересованы в точной настройке на одном графическом процессоре и хотите, чтобы точно настроенная модель соответствовала производительности стандартной точной настройки на нескольких графических процессорах, то QLoRA — это то, что вам нужно.
Надеюсь, это была полезная информация о QLoRA. Увидимся в следующем. А пока берегите себя.
Также опубликовано здесь. эм>
Оригинал

