
Доказательства и понимание экспериментов по причинной кластеризации в условиях сетевых помех
1 февраля 2024 г.:::информация Авторы:
(1) Давиде Вивиано, факультет экономики Гарвардского университета;
(2) Лихуа Лэй, Высшая школа бизнеса Стэнфордского университета;
(3) Гвидо Имбенс, Высшая школа бизнеса и факультет экономики Стэнфордского университета;
(4) Брайан Каррер, FAIR, Meta;
(5) Окке Шрийверс, Meta Central Applied Science;
(6) Лян Ши, Meta Central Applied Science.
:::
Таблица ссылок
(Когда) следует кластеризовать?
Эмпирические иллюстрации и численные исследования
Доказательства C
На протяжении всех доказательств ожидания зависят от матрицы смежности A.
C.1 Доказательство леммы 3.1
У нас есть

В.2 Доказательство леммы 3.2

В.3 Доказательство леммы 3.3
Мы рассматриваем случай, когда два объекта находятся в одном или разных кластерах по отдельности. Для удобства обозначений мы будем называть µi(Di , D−i) µi(D).


Выполнив те же действия, что и в случае, когда i, j находятся в разных кластерах, с учетом уравнения (27), доказательство завершается.
В.4 Доказательство леммы 3.4
другие единицы не равны нулю для индивидуумов в множествах Bi, Gi, определенных в лемме 3.2.

где первое неравенство обусловлено неравенством Коши-Шварца, а последнее равенство следует из предположения 5. Доказательство завершается после сбора членов.
C.5 Доказательство теоремы 3.5


C.6 Доказательство теоремы 3.6

C.7 Доказательство теоремы 4.1
Смещение следует непосредственно из леммы 3.1. Теперь мы обсудим компонент дисперсии. Учитывая леммы 3.2, 3.3 и следуя уравнениям (28), (29), можно написать
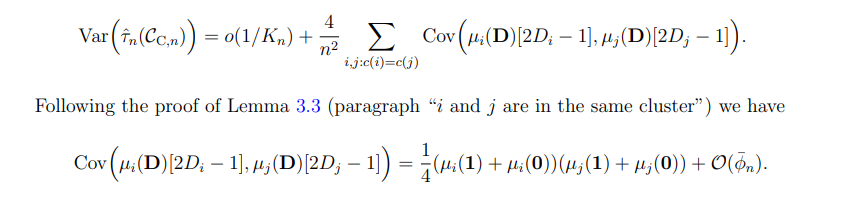

C.8 Доказательство теоремы 4.2

C.9 Доказательство теоремы 4.3

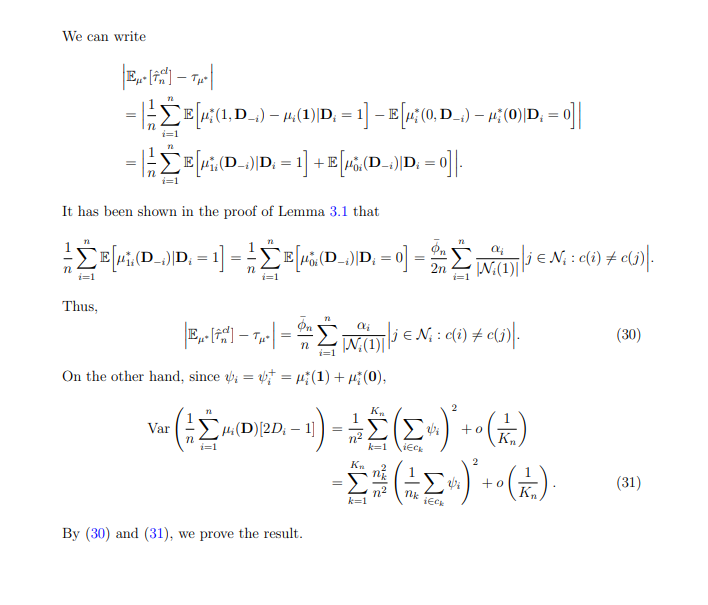
:::информация Этот документ доступен на arxiv по лицензии CC 1.0.
:::
Оригинал

