Перекрывающиеся прямоугольники: ежедневная проблема кодирования

Добро пожаловать, вам предстоит решить еще одну проблему! Сегодня мы имеем дело с небольшой геометрией и перекрывающимися прямоугольниками с этой интересной задачей: первой в 2024 году! Приветствую всех! 🎉

Даже если это простая проблема, для ее решения потребовался довольно большой объем кода, и я не совсем уверен, что это лучший подход для ее решения.

Итак, как всегда, не стесняйтесь ответить на свое решение, если вы хотите обсудить это дальше!

Как всегда, эту проблему предоставил замечательный информационный бюллетень Daily Coding Issue, на который вы можете подписаться здесь! Посмотрите это и попробуйте решить свои проблемы!

Итак, пока мы ждем, пока мое произведение искусства получит заслуженную цену, давайте перейдем к проблеме!

Проблема

==Дано два прямоугольника на двумерном графике, вернуть площадь их пересечения. Если прямоугольники не пересекаются, верните 0.==

==Например, для следующих прямоугольников:==

{
    "top_left": (1, 4),
    "dimensions": (3, 3) # width, height
}

==и==

{
    "top_left": (0, 5),
    "dimensions": (4, 3) # width, height
}

==возврат 6.==

Проблема довольно ясна: нам даны размеры и координаты двух прямоугольников. Нас просят вычислить площадь пересечения: если ее нет, мы должны просто вернуть 0.

Давайте сначала нарисуем планы!

План

Давайте нарисуем два перекрывающихся прямоугольника, как показано в примере.

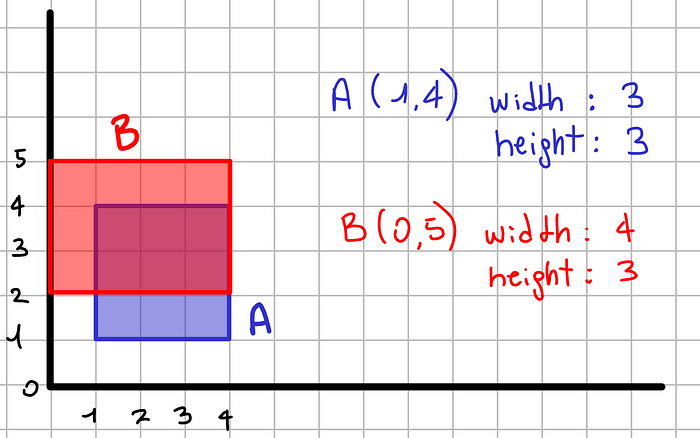
Поскольку мы находимся на графике, мы можем рассматривать подобные фигуры как набор точек. Например, синий прямоугольник A представляет собой совокупность следующих точек: (1,4) (2,4) (3,4) (4,4) (1,3) (2,3) … (3, 1) (4,1). Ту же идею можно применить и к другому прямоугольнику таким же образом.

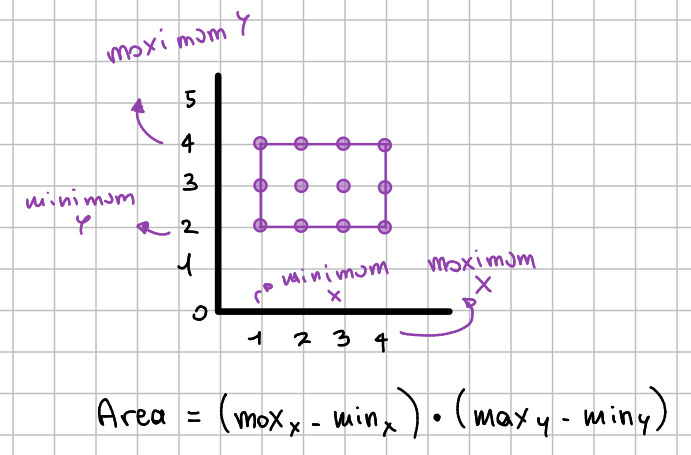
Таким образом, мы можем легко идентифицировать точки пересечения, просматривая, какие точки появляются в обоих прямоугольниках, как показано фиолетовым цветом ниже.

Собрав точки, мы можем легко вычислить длины сторон и размер области перекрытия.

Перейдем к коду. На этот раз будет Го, так что пристегните ремни: путешествие будет долгим и многословным!

Кодекс

Давайте, как обычно, пройдемся по коду шаг за шагом:

https://gist.github.com/NicolaM94/32290881cf90b365564f28459ad5ab82?embedable = правда #file-main-go

Во-первых, мы создаем struct для нашего прямоугольника с некоторыми свойствами, а именно startingX, startY, width, height , которые задаются текстом задачи.

После этого пишем метод для нашей структуры. Не дайте себя обмануть ключевым словом func: после этого слова объявляется тип структуры; это просто синтаксис построения методов Go.

Этот метод под названием Points , который возвращает массив целых чисел ( out [][]int ), будет использоваться для сбора… ну, координат точек прямоугольника. : кто бы мог подумать!

Чтобы вычислить точки, мы просто итерируем от точки к точке, собирая их одну за другой и временно сохраняя в переменную couple, которая очищается в каждом цикле.

Эта переменная также будет добавлена ​​к массиву out в каждом цикле, чтобы мы могли вернуть все в конце.

В основной функции мы инициализируем два прямоугольника и вычисляем их точки.

Теперь нам нужна функция для сбора общих точек: давайте ее напишем!

https://gist.github.com/NicolaM94/0f9826a99162b2ca2978149b9943bd4f?emb съедобный = правда #file-main-go

Функция CommonPoints принимает два экземпляра Rectangle, расположенные по их точкам. Если две точки имеют одинаковые координаты, эта точка добавляется в out для сбора.

Мы также обновили функцию main, чтобы распечатать эти общие точки.

Наконец, мы можем вычислить площадь: функция CalcAreaFromPoints делает именно это.

https://gist.github.com/NicolaM94/0dda69b1f877e3797fc213d1a52c22be?embedable = правда #file-main-go

Функция изначально оценивает длину массива, содержащего общие точки: если она равна нулю, общих точек нет, то есть прямоугольники не перекрываются.

После этого функция собирает четыре необходимые переменные, minX, maxX, minY, maxY, перебирая координаты точки и сравнивая их. Как только они собраны, размер общей области можно просто указать как (maxX — minX)*(maxY-minY) .

Нам нужно обновить нашу основную функцию в последний раз, чтобы распечатать область общих точек.

Временная сложность

Временная сложность этого алгоритма особенно болезненна, поскольку он переполнен квадратичным временем.

* Нам нужно набирать точки, а для их сбора нам нужно перемещаться по двум измерениям прямоугольника. Это ограничит нас квадратичной временной сложностью.

* Нам нужно собрать общие точки в пределах двух прямоугольников. По той же причине, что и выше, на этот раз мы ограничены квадратом временной сложности.

По указанным выше причинам временная сложность этого алгоритма в целом равна O(n²). Как я уже упоминал выше, я почти уверен, что для этого существуют лучшие или более быстрые алгоритмы: если вы знаете какой-либо алгоритм или просто хотите поделиться своим мнением, не стесняйтесь делать это в комментариях!

Заключение

Вот и все! Как всегда, я хочу поблагодарить вас за то, что дочитали до этого момента: если статья вам понравилась или оказалась полезной, пожалуйста, поставьте лайк или два; это действительно сделало бы мой день! Кроме того, если вы можете и если вы хотите, вы можете поддержать мою работу здесь, поделившись со мной Ko-Fi здесь< /a>!

Как всегда, спасибо за внимание.

Никола