О силлогизме.
1 ноября 2023 г.Логическое исчисление Джорджа Буля входит в серию книг HackerNoon. Вы можете перейти к любой главе этой книги здесь. О силлогизме.
О силлогизме.
Уже выведенные формы категорических суждений суть
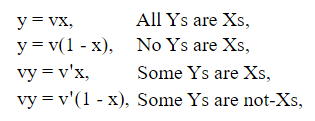
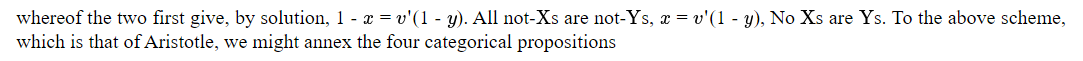

два первых из которых аналогичным образом конвертируются в
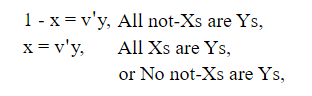 n Если теперь две посылки любого силлогизма выражаются уравнениями вышеуказанных форм, то устранение общий символ y приведет нас к уравнению, выражающему вывод.
n Если теперь две посылки любого силлогизма выражаются уравнениями вышеуказанных форм, то устранение общий символ y приведет нас к уравнению, выражающему вывод.
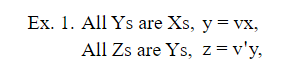
исключение y дает
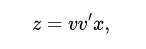
интерпретация которого
n 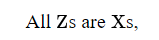
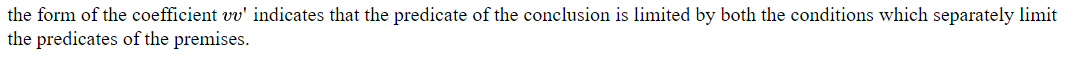
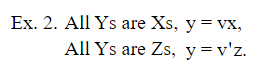
исключение y дает
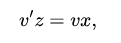
что можно интерпретировать как Некоторые Z — это X. Всегда необходимо, чтобы один член заключения можно было интерпретировать посредством уравнений посылок. В приведенном выше случае оба варианта таковы.
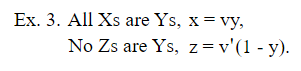
Вместо прямого исключения y позвольте любому уравнению быть преобразовано путем решения, как в (19). Первый дает
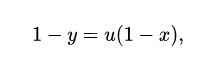
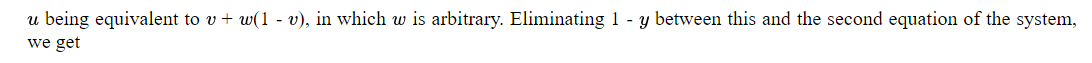
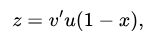
интерпретация которого
Никакие Z не являются X.
Если бы мы напрямую исключили y, у нас должно было бы получиться
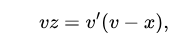
сокращенное решение которого
n 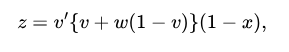
в котором w — произвольный выборный символ. Это точно согласуется с предыдущим результатом.
Этих примеров может быть достаточно, чтобы проиллюстрировать применение метода в конкретных случаях. Но ее применимость для доказательства общих теорем является здесь, как и в других случаях, более важной особенностью. Присоединяю результаты недавнего исследования законов силлогизма. Хотя эти результаты характеризуются большой простотой и практически не содержат следов своего математического происхождения, я полагаю, что было бы очень трудно прийти к ним путем рассмотрения и сравнения частных случаев.
О книжной серии HackerNoon: мы предлагаем вам наиболее важные технические, научные и познавательные книги, являющиеся общественным достоянием.
Эта книга является общественным достоянием. Джордж Буль (2022). Логическое исчисление. Урбана, Иллинойс: Проект Гутенберг. Получено в октябре 2022 г. https://www.gutenberg.org/cache/epub/69512/pg69512-images. .html
Эта электронная книга предназначена для использования кем угодно и где угодно, бесплатно и практически без каких-либо ограничений. Вы можете скопировать ее, отдать или повторно использовать в соответствии с условиями лицензии Project Gutenberg, включенной в данную электронную книгу или на сайте www.gutenberg.org, расположен по адресу https://www.gutenberg.org/policy/license.html.
Оригинал

