Обязательные базовые советы по разработке функций с данными временных рядов

Введение

Данные временных рядов, состоящие из точек данных, расположенных в хронологическом порядке, необходимы в различных секторах, таких как финансы, здравоохранение и метеорология.

Искусство разработки признаков, при котором новые признаки получаются из существующих данных, является важным аспектом разработки точных и надежных прогностических моделей.

В этой статье мы обсудим некоторые важные базовые советы по разработке функций с данными временных рядов, которые помогут вам использовать весь потенциал ваших данных и повысить производительность ваших моделей машинного обучения.

Мы углубимся в функции даты и времени, функции, специфичные для предметной области, функции задержки, функции скользящего и расширяющегося окна, экспоненциальное сглаживание и сезонную декомпозицию.

Освоив эти методы, вы сможете лучше подготовиться к выявлению скрытых закономерностей, тенденций и взаимосвязей в ваших данных временных рядов и повысите способность вашей модели делать точные прогнозы.

Советы

1. Функции даты и времени и функции для конкретных доменов

Данные временных рядов часто содержат временные метки, предоставляющие ценную информацию о данных.

Извлечение функций даты и времени, таких как день, месяц, год, день недели и час, может помочь повысить производительность модели за счет захвата закономерностей и тенденций, связанных с этими временными компонентами.

Сезонность, праздничные и выходные дни — это примеры циклических закономерностей, которые можно идентифицировать с помощью функций даты и времени.

Включение функций, специфичных для предметной области, может значительно повысить производительность модели машинного обучения. Специфические для предметной области функции получены из экспертных знаний в соответствующей области и могут предоставить ценную информацию, которой нет в необработанных данных временных рядов.

Например, в финансах индекс волатильности или другие экономические индикаторы можно использовать в качестве дополнительных функций для улучшения прогнозирования цен на акции.

Вот пример моей собственной функции, которая широко использовалась в практике квантовых хедж-фондов:

def extract_date_features(data):
    data['Year'] = data.index.year
    data['Month'] = data.index.month
    data['Day'] = data.index.day
    data['Weekday'] = data.index.weekday
    data['Day_of_year'] = data.index.dayofyear
    data['Week_of_year'] = data.index.isocalendar().week
    data['Quarter'] = data.index.quarter
    data['Is_month_start'] = data.index.is_month_start
    data['Is_month_end'] = data.index.is_month_end
    data['Is_quarter_start'] = data.index.is_quarter_start
    data['Is_quarter_end'] = data.index.is_quarter_end
    data['Is_year_start'] = data.index.is_year_start
    data['Is_year_end'] = data.index.is_year_end
    data['Days_in_month'] = data.index.days_in_month
    data['Is_leap_year'] = data.index.is_leap_year
    data['Elapsed_days'] = (data.index - data.index.min()).days
    data['Weekday_name'] = data.index.day_name()
    data['Month_name'] = data.index.month_name()
    data['Is_weekend'] = data['Weekday'].apply(lambda x: x >= 5)
    data['Is_weekday'] = ~data['Is_weekend']
    data['Days_till_month_end'] = data['Days_in_month'] - data['Day']
    data['Days_since_month_start'] = data['Day'] - 1
    data['Week_of_month'] = (data['Day'] - 1) // 7 + 1
    data['Weekday_of_month'] = (data['Day'] - 1) % 7 + 1
    data['Days_to_next_holiday'] = data.index.to_series().apply(lambda x: (x + pd.DateOffset(days=1)).to_period('D').start_time)
    data['Days_since_last_holiday'] = data.index.to_series().apply(lambda x: (x - pd.DateOffset(days=1)).to_period('D').end_time)
    data['Business_days_in_month'] = data.index.to_series().apply(lambda x: np.busday_count(x.replace(day=1), x.replace(day=x.days_in_month) + pd.DateOffset(days=1)))
    data['Business_day_of_month'] = data.index.to_series().apply(lambda x: np.busday_count(x.replace(day=1), x))
    data['Days_since_first_day_of_year'] = data['Day_of_year'] - 1
    data['Days_remaining_in_year'] = (data.index + pd.offsets.YearEnd(0)).dayofyear - data['Day_of_year']

    return data

data = extract_date_features(data)
print(data.head())

2. Функции отставания

Функции запаздывания относятся к значениям предыдущих временных шагов во временном ряду. Они могут помочь зафиксировать автокорреляцию, присутствующую в данных, которая представляет собой отношение между текущим значением и его прошлыми значениями.

Добавление запаздывающих функций может повысить производительность модели, позволяя ей изучать шаблоны из прошлого для прогнозирования будущих значений. Вы можете создавать функции задержки, сдвигая исходные данные временного ряда на определенное количество периодов, часто называемое "порядком задержки".

import pandas as pd

def create_lag_features(data, n_lags):
    data_frame = pd.DataFrame(data, columns=['value'])
    for i in range(1, n_lags+1):
        data_frame[f'lag_{i}'] = data_frame['value'].shift(i)
    return data_frame

time_series = [100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200]
n_lags = 3
lag_features = create_lag_features(time_series, n_lags)

#Result:

   value  lag_1  lag_2  lag_3
0    100    NaN    NaN    NaN
1    110  100.0    NaN    NaN
2    120  110.0  100.0    NaN
3    130  120.0  110.0  100.0
4    140  130.0  120.0  110.0
5    150  140.0  130.0  120.0
6    160  150.0  140.0  130.0
7    170  160.0  150.0  140.0
8    180  170.0  160.0  150.0
9    190  180.0  170.0  160.0
10   200  190.0  180.0  170.0

3. Свертывание и расширение функций Windows

Статистика скользящего окна и расширяющегося окна включает в себя вычисление сводной статистики, такой как среднее значение, медиана, стандартное отклонение, а также максимальное или минимальное значение в движущемся или постепенно увеличивающемся окне фиксированного размера.

Эти функции помогают фиксировать локальные тенденции, колебания и общее поведение данных временных рядов, позволяя модели учиться на основе временной динамики. Статистика скользящего окна может быть особенно полезна при работе с зашумленными данными или когда временной ряд демонстрирует нестационарность.

С другой стороны, расширение окон может дать представление о кумулятивных эффектах или долгосрочных тенденциях в данных. Как скользящую, так и расширяющуюся статистику окна можно легко реализовать с помощью функций скользящего и расширяющегося окна, доступных в библиотеке pandas.

Пример кода:

# Apply a rolling window
window_size = 3
time_series['Rolling_Mean'] = time_series['Data'].rolling(window=window_size).mean()
time_series['Rolling_Std'] = time_series['Data'].rolling(window=window_size).std()

# Apply an expanding window
time_series['Expanding_Mean'] = time_series['Data'].expanding().mean()
time_series['Expanding_Std'] = time_series['Data'].expanding().std()

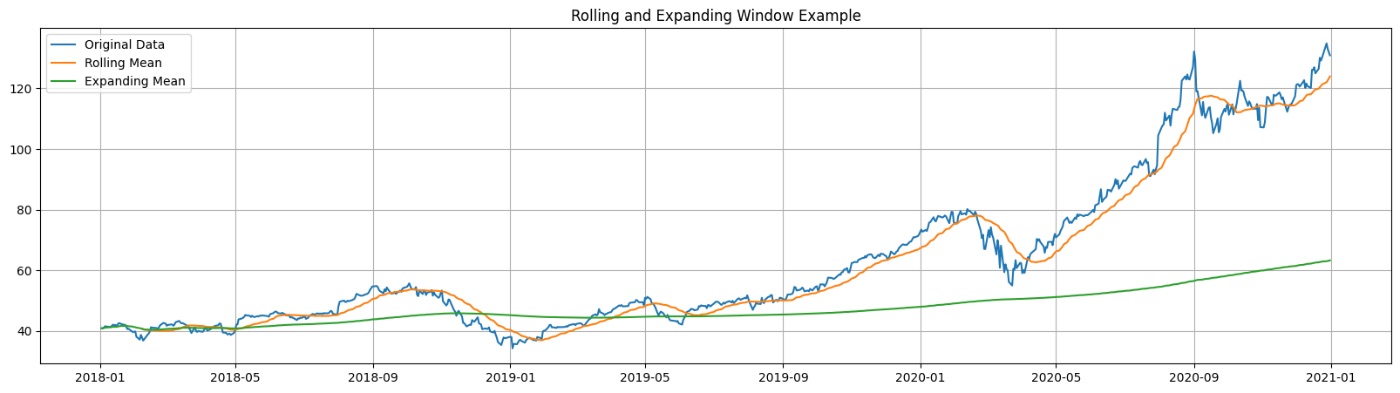
# Visualize the results
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(time_series['Date'], time_series['Data'], label='Original Data', marker='o')
ax.plot(time_series['Date'], time_series['Rolling_Mean'], label='Rolling Mean', marker='o')
ax.plot(time_series['Date'], time_series['Expanding_Mean'], label='Expanding Mean', marker='o')
ax.legend(loc='best')
ax.set_title('Rolling and Expanding Window Example')
plt.show()

4. Экспоненциальное сглаживание

Экспоненциальное сглаживание – это метод, при котором прошлым наблюдениям присваивается экспоненциально убывающий вес, при этом больший акцент делается на недавних наблюдениях. Этот подход может быть полезен для уменьшения шума и выявления тенденций в данных временных рядов.

Существуют различные формы экспоненциального сглаживания, такие как простое экспоненциальное сглаживание, двойное экспоненциальное сглаживание (метод Холта) и тройное экспоненциальное сглаживание (метод Холта-Уинтерса), которые можно использовать на основе характеристик данных временных рядов.

* Простое экспоненциальное сглаживание — еще один метод, используемый для сглаживания данных временных рядов. Он присваивает экспоненциально уменьшающиеся веса прошлым наблюдениям, придавая большее значение последним точкам данных. Формула экспоненциального сглаживания:

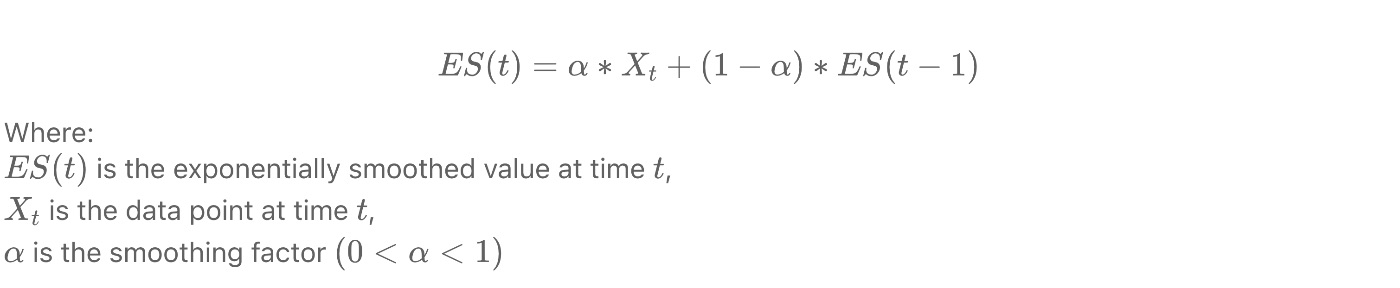
Где ES(t) — экспоненциально сглаженное значение в момент времени t, X_t — точка данных в момент времени t, а α — коэффициент сглаживания (0 < α < 1).

Простой пример Python:

def exponential_smoothing(data, alpha):
    es = [data[0]]
    for t in range(1, len(data)):
        es.append(alpha * data[t] + (1 - alpha) * es[t - 1])
        return es

• Холт-Уинтерс – это метод прогнозирования, расширяющий возможности простого метода экспоненциального сглаживания и учитывающий сезонность и тенденции. Метод состоит из трех компонентов: уровень (сглаживание ряда), тренд (сглаживание тренда) и сезонность (сезонный компонент).

Существует два варианта метода: аддитивный и мультипликативный.

Пример кода Холта-Уинтерса:

from statsforecast.models import HoltWinters
from statsforecast.utils import AirPassengers as ap


model = HoltWinters(season_length=12, error_type='A')
model = model.fit(y=ap)
y_hat_dict = model.predict(h=4)
y_hat_dict

5. Сезонное разложение

Сезонная декомпозиция – это метод разделения временного ряда на трендовые, сезонные и остаточные компоненты. Наиболее распространенным методом сезонной декомпозиции является метод STL (сезонная и трендовая декомпозиция с использованием лесса).

Пример кода для сезонной декомпозиции с использованием традиционной библиотеки statsmodels:

import statsmodels.api as sm
import matplotlib.pyplot as plt

data = np.array([...])
# Input time series data
seasonal_period = 12
result = sm.tsa.seasonal_decompose(data, period=seasonal_period)
trend = result.trend
seasonal = result.seasonal
residual = result.resid
result.plot()
plt.show()

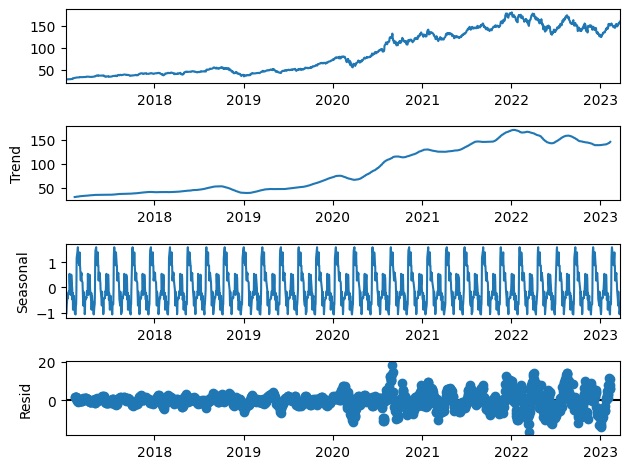
Дополнительный пример кода для сезонной декомпозиции с использованием библиотеки statsforecast:

from statsforecast import StatsForecast
from statsforecast.models import MSTL, AutoARIMA
import matplotlib.pyplot as plt

models = [
    MSTL(
        season_length=[12 * 7],  # seasonalities of the time series
        trend_forecaster=AutoARIMA(),  # model used to forecast trend
    )
]

sf = StatsForecast(
    models=models,  # model used to fit each time series
    freq="D",  # frequency of the data
)
sf = sf.fit(data)
test = sf.fitted_[0, 0].model_
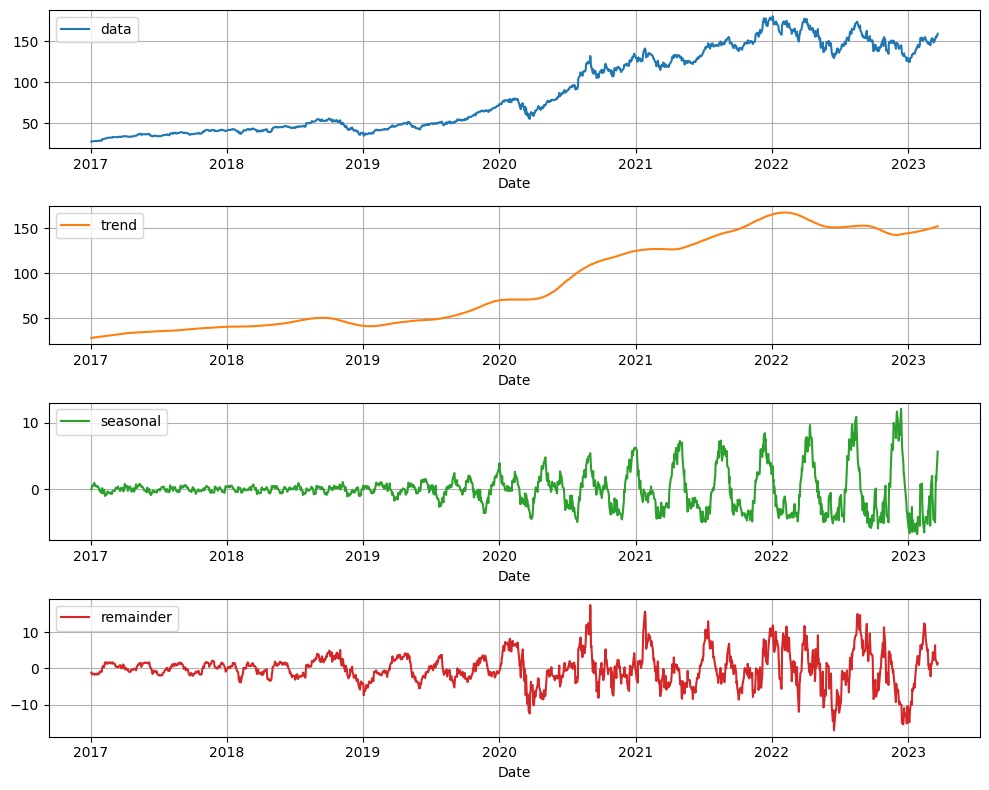
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
test.plot(ax=ax, subplots=True, grid=True)
plt.tight_layout()
plt.show()

Заключение

Данные временных рядов незаменимы в различных отраслях, и проектирование признаков играет ключевую роль в разработке точных и надежных прогностических моделей.

В этой статье мы обсудили основные методы разработки признаков с данными временных рядов, такие как извлечение признаков даты и времени, включение признаков, специфичных для предметной области, создание признаков задержки, использование скользящих и расширяющихся оконных функций, реализация экспоненциального сглаживания и выполнение сезонной декомпозиции. .

Освоив эти подходы, вы сможете лучше использовать весь потенциал данных временных рядов и повысить способность модели делать точные прогнозы.

Помните, что каждый набор данных временных рядов уникален, и очень важно адаптировать свои стратегии разработки признаков к вашей конкретной предметной области.

Поэкспериментируйте с различными методами, комбинациями и параметрами, чтобы выявить скрытые закономерности и взаимосвязи в ваших данных и создать модели, которые лучше подходят для решения задач в вашей конкретной области.

Таким образом вы сможете полностью раскрыть потенциал данных временных рядов и создать более надежные и точные прогностические модели.