Прогнозирование с несколькими точками: освоение алгоритмических рассуждений с расширенным использованием ресурсов
deep-learning tech-stories multi-token-prediction ai-reasoning algorithmic-reasoning pause-tokens llm-optimization computation-sharing ai-theory

Прогнозирование с несколькими точками: освоение алгоритмических рассуждений с расширенным использованием ресурсов

25 июля 2025 г.

Аннотация и 1. Введение

2. Метод

3. Эксперименты по реальным данным

4. Абляции на синтетических данных

5. Почему это работает? Некоторые предположения

6. Связанная работа

7. Заключение, Заявление о воздействии, воздействие на окружающую среду, подтверждения и ссылки

A. Дополнительные результаты по самопрокативному декодированию

Б. Альтернативные архитектуры

C. Скорость тренировок

D. МАГАЗИН

E. Дополнительные результаты по поведению масштабирования модели

F. Подробности о CodeContests Manetuning

G. Дополнительные результаты по сравнению с естественным языком

H. Дополнительные результаты по абстрактному текстовому суммированию

I. Дополнительные результаты по математическим рассуждениям на естественном языке

J. Дополнительные результаты по индукционному обучению

K. Дополнительные результаты по алгоритмическим рассуждениям

L. Дополнительные интуиции по многоцелевым прогнозам

М. Обучение гиперпараметры

K. Дополнительные результаты по алгоритмическим рассуждениям

Мы исследуем следующееГипотеза обмена вычислениямиДля объяснения эффективности многоцветного прогнозирования в качестве потери тренировок.

Сложность предсказания разных токенов в естественном тексте сильно варьируется. Некоторые токены могут быть продолжением частичных слов, которые уникально определены из их предыдущего контекста без каких -либо усилий, в то время как другим может потребоваться предсказать имена теорем в сложных математических доказательствах или правильный ответ на экзамен. Было показано, что языковые модели с остаточными соединениями уточняют распределение их выходных токков с каждым последовательным уровнем и могут быть обучены стратегии раннего выхода, которые тратят переменные объемы вычислительных ресурсов на позицию токена. Потеря с мульти-токеном прогнозирования явно поощряют обмен информацией между соседними позициями токена и, таким образом, могут рассматриваться как метод для изучения распределения вычислительных ресурсов в языковых моделях более эффективно для токенов, которые приносят пользу большей части.

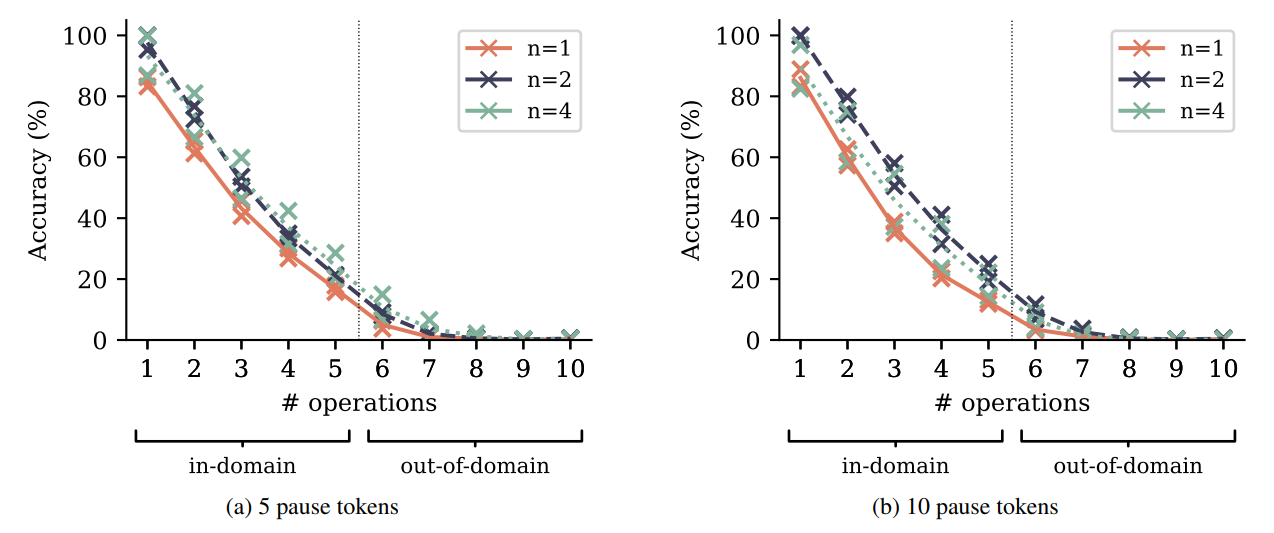
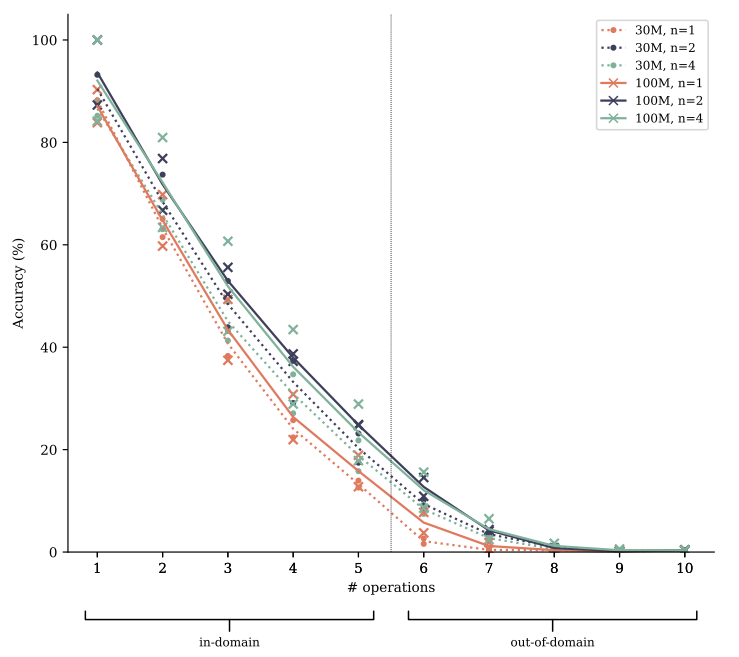
Чтобы проверить истину этой гипотезы, мы увеличиваем полиномиальную арифметическую задачу из Раздела 4.2 с различным числомТокены паузы(Goyal et al., 2023) вставлен между вопросом и токеном, который обозначает начало ответа. Токены Pause вводят дополнительные вычислительные ресурсы, которые могут быть потрачены на вычисления, которые, как ожидается, будут полезны позже в последовательности, другими словами: чтобы начать думать об ответе. СогласноГипотеза обмена вычислениями, Модели предсказания с несколькими токками изучают обмен информацией и, следовательно, обмен вычислениями между позициями токенов легче, и могут лучше использовать эти дополнительные вычислительные ресурсы, чем модели прогнозирования следующих ток. На рисунке S15 мы показываем результаты оценки по полиномиальной арифметической задаче с фиксированным количеством токенов паузы, вставленных как во время обучения, так и во время обучения. Модели предсказания с несколькими ток-точками также превосходят модели прогнозирования следующего ток на этих вариантах задач по трудностям и размерам моделей. Тем не менее, мы не видим убедительных доказательств расширения или сокращения этого разрыва, то есть мы не можем заключить из этих экспериментов о достоверности гипотезы обмена вычислениями.

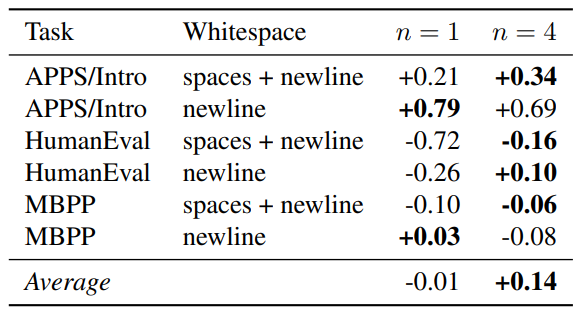
В таблице S11 мы сообщаем о результатах другого эксперимента в том же духе: добавляя пробелы и новички в Humaneval и MBPP подсказки, мы добавляем «токены паузы» несколько естественным образом. Согласно этим результатам, модели предсказания с несколькими точками имеют небольшое преимущество при использовании этого дополнительно предоставленного вычисления, но эффект является незначительным.

Figure S15: Accuracy on a polynomial arithmetic task with varying number of operations per expression and pause tokens. We train and evaluate models on the polynomial arithmetic task described in Section 4.2, modified by the addition of pause tokens (Goyal et al., 2023): between the question and the equality sign that indicates the beginning of the answer, we add a constant number of pause tokens both in training and evaluation. For both a variant with five and with ten pause tokens, respectively, we observe comparable improvements from using multi-token prediction to the ones obtained in the case without pause tokens (Figure 8).

Table S11: Utilization of additional whitespace tokens in code benchmarks.

Figure S16: Accuracy on a polynomial arithmetic task for two model sizes. We train and evaluate models with 30M and 100M parameters on the polynomial arithmetic task described in Section 4.2. Tripling the model size has a smaller effect on performance than replacing next-token prediction loss by multi-token prediction. Shown are two independent runs per configuration and their means, the 100M parameter models being identical to the ones in Figure 8.

Table S12: Optimal temperatures for all numbers in table 1

Авторы:

(1) Фабиан Глокл, ярмарка в Meta, Cermics Ecole des Ponts Paristech и равный вклад;

(2) Badr Youbi Idrissi, Fair at Meta, Lisn Université Paris-Saclayand и равный вклад;

(3) Baptiste Rozière, ярмарка в Meta;

(4) Дэвид Лопес-Паз, ярмарка в Meta и последний автор;

(5) Габриэль Синнев, ярмарка в Meta и последний автор.

Эта статья естьДоступно на ArxivПод CC по лицензии 4.0.

Оригинал

Recent Post

Categories

PREVIOUS ARTICLE
NEXT ARTICLE