
Предсказание с несколькими точками: управление качественными изменениями в возможностях LLM
6 июня 2025 г.Таблица ссылок
Аннотация и 1. Введение
2. Метод
3. Эксперименты по реальным данным
3.1. Шкала преимуществ с размером модели и 3,2. Более быстрый вывод
3.3. Изучение глобальных моделей с помощью мульти-байтового прогноза и 3.4. Поиск оптимальногоне
3.5. Обучение для нескольких эпох и 3.6. Создание нескольких предикторов
3.7 Многократный прогноз на естественном языке
4. Абляции на синтетических данных и 4.1. Индукционная способность
4.2. Алгоритмические рассуждения
5. Почему это работает? Некоторые спекуляции и 5.1. Lookahead Укрепляет очки выбора
5.2. Информация теоретичный аргумент
6. Связанная работа
7. Заключение, Заявление о воздействии, воздействие на окружающую среду, подтверждения и ссылки
A. Дополнительные результаты по самопрокативному декодированию
Б. Альтернативные архитектуры
C. Скорость тренировок
D. МАГАЗИН
E. Дополнительные результаты по поведению масштабирования модели
F. Подробности о CodeContests Manetuning
G. Дополнительные результаты по сравнению с естественным языком
H. Дополнительные результаты по абстрактному текстовому суммированию
I. Дополнительные результаты по математическим рассуждениям на естественном языке
J. Дополнительные результаты по индукционному обучению
K. Дополнительные результаты по алгоритмическим рассуждениям
L. Дополнительные интуиции по многоцелевым прогнозам
М. Обучение гиперпараметры
4. Абляции на синтетических данных
Что способствует улучшениям в производительности нисходящих моделей многоцветного прогнозирования во всех рассматриваемых мы заданиях? Проведя эксперименты по игрушкам на контролируемых наборах данных обучающих данных и задачах оценки, мы демонстрируем, что многократный прогноз приводит к качественным изменениям в возможностях модели и поведении обобщения. В частности, раздел 4.1 показывает, что для небольших размеров модели индукционная способность - как обсуждается Olsson et al. (2022)-либо формируются только при использовании многоцветного прогнозирования в качестве потери тренировок, или он значительно улучшается. Более того, раздел 4.2 показывает, что многоцветный прогноз улучшает обобщение арифметической задачи, даже больше, чем размер утроения модели.
4.1. Индукционная способность
Индукция описывает простую схему рассуждений, которая завершает частичные закономерности благодаря их последнему продолжению (Olsson et al., 2022). Другими словами, если предложение содержит «AB», а затем упоминает «A», индукция - это прогноз, что продолжение «B». Мы разрабатываем установку для измерения индукции

Возможности контролируемым образом. Обучение небольших моделей размеров от 1 млн до 1B Параметры не внедренных параметров на наборе данных о детских историях, мы измеряем возможность индукции с помощью адаптированного набора тестов: В 100 этажах из исходного разделения тестов мы заменяем имена символов случайно сгенерированными именами, которые состоят из двух токенов с токенизатором, который мы используем. Прогнозирование первого из этих двух токенов связано с семантикой предыдущего текста, в то же время предсказывая второй токен возникновения каждого имени после того, как оно упоминалось, по крайней мере, один раз можно рассматривать как задачу для чистой индукции. В наших экспериментах мы тренируемся до 90 эпох и выполняем раннюю остановку в отношении испытательной метрики (то есть мы разрешаем эпоху Oracle). На рисунке 7 представлена индукция, измеренная точностью на вторых токенах имен по отношению к размеру модели для двух прогонов с разными семенами.
Мы обнаруживаем, что потеря прогнозирования с двумя точками приводит к значительно улучшенной формированию индукционной способности для моделей параметров неэмблинга размером 30 м и ниже, с их преимуществом, исчезающим для размеров параметров не внесения 100 м и выше. [1] Мы интерпретируем этот вывод следующим образом: потери с множественными прогнозами помогают моделям изучения передачи информации по положениям последовательностей, что поддается формированию индукционных голов и других встроенных механизмов обучения. Однако, как только сформировались индукционные возможности, эти изученные особенности преобразуют индукцию
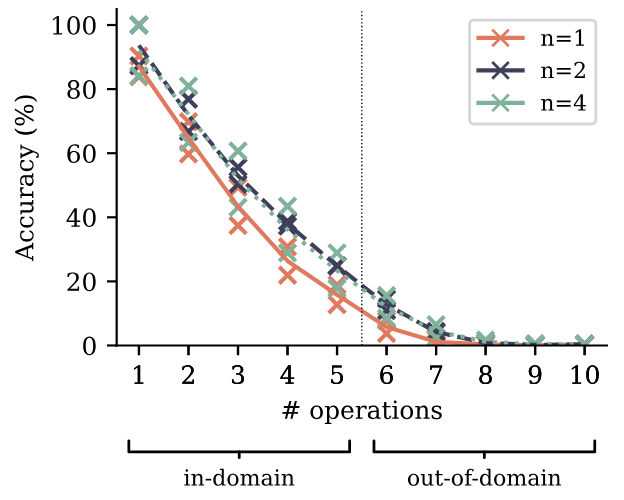
в задачу, которая может быть решена локально в текущем токене и изучена только с следующим предсказанием. С этого момента, многократный прогноз на самом деле больно в этом ограниченном эталоне, но мы предполагаем, что существуют более высокие формы рассуждений в контексте, в которые он дополнительно способствует, о чем свидетельствуют результаты в разделе 3.1. На рисунке S14 мы предоставляем доказательства этого объяснения: замена набора данных о детских историях на более высокий качественный сочетаний 9: 1 набор данных книг с детскими историями, мы обеспечиваем формирование индукционных возможностей в начале обучения только с помощью набора данных. В результате, за исключением двух наименьших размеров модели, преимущество многоцелового прогнозирования в задаче исчезает: обучение функциям индукционных функций преобразовало задачу в чистую задачу предсказания следующего ток.
Эта статья естьДоступно на ArxivПод CC по лицензии 4.0.
[1] Обратите внимание, что идеальная оценка не доступна в этом эталонном эталоне, поскольку некоторые токены в именах в наборе данных оценки никогда не появляются в учебных данных, а в нашей архитектуре параметры встраивания и неэмбенции не связаны.
Авторы:
(1) Фабиан Глокл, ярмарка в Meta, Cermics Ecole des Ponts Paristech и внес свой вклад;
(2) Badr Youbi Idrissifair в Meta, Lisn Université Paris-Saclay и внес свой вклад;
(3) Baptiste Rozière, ярмарка в Meta;
(4) Дэвид Лопес-Паз, ярмарка в Мете и его последний автор;
(5) Габриэль Синнев, ярмарка в Meta и последний автор.
Оригинал

