Моделирование Монте-Карло для устойчивой системы репутации, основанной на блокчейне
2 января 2024 г.:::информация Этот документ доступен на arxiv по лицензии CC BY-NC-SA 4.0 DEED.
Авторы:
(1) Х. Вэнь, факультет экономики, Университет Бата;
(2) Т. Хуанг, факультет бизнеса и права, Университет Рохэмптона;
(3) Д. Сяо, Школа математических наук.
:::
Таблица ссылок
Соответствующие технологии блокчейна
Расширенные модели для реальных сценариев
5. Моделирование Монте-Карло
После тщательного построения наших моделей в предыдущих разделах теперь необходимо подвергнуть их тщательному моделированию и выяснить, соответствуют ли их характеристики нашим ожиданиям. Центральное место в нашей методологии моделирования занимает известная методика Монте-Карло. Мы начинаем наше путешествие с краткого введения в моделирование Монте-Карло, подготавливая почву для новичков и закрепляя наши подходы на теоретической основе. Затем мы углубимся в общие настройки моделирования системы репутации по методу Монте-Карло, определив параметры и конфигурации, необходимые для наших экспериментов. Впоследствии исследуются два противоположных сценария начального распределения кредитов: один, где сценарий кредитных баллов первоначально равномерно распределен между агентами, и другой, в котором выделяется сценарий кредитных баллов, первоначально распределенных по степенному закону между агентами. По мере того, как мы углубляемся в результаты моделирования, наше внимание разделяется на два сегмента: «Результаты и интерпретации моделирования Монте-Карло для базовой модели» и «Результаты и интерпретации моделирования Монте-Карло для расширенных моделей», каждый из которых проливает свет на результаты соответствующих моделей и проводить сравнения там, где это необходимо.
<ем>5.1. Краткое введение в моделирование Монте-Карло
Моделирование Монте-Карло (MCS) [80] — мощный статистический метод, позволяющий использовать вероятностный подход к пониманию сложных систем. По сути, MCS использует случайную выборку и статистический анализ для приблизительного решения математических задач.
<ем>5.1.1. Основные принципы
Основная концепция MCS проста: выполнив достаточно большое количество случайных симуляций или «испытаний», можно получить аппроксимацию желаемой величины. Математически возьмем случайную величину X с ожидаемым значением E[X]. Оценка E[X] по методу Монте-Карло:
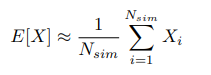

<ем>5.1.2. Применение к структурной надежности
В структурном проектировании, откуда берет свое начало MCS [81], MCS стала важным инструментом для оценки надежности конструкций. Давайте рассмотрим функцию предельного состояния (LSF) G(x), которая очерчивает границу между неудачным и успешным состояниями конструкции. Типичное представление:
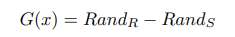
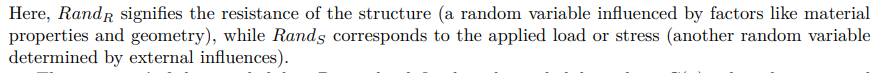
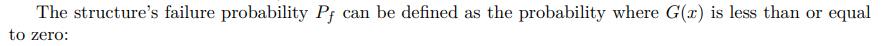
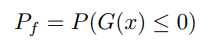
Чтобы оценить вероятность отказа с помощью MCS, можно:

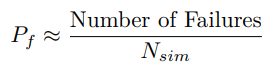

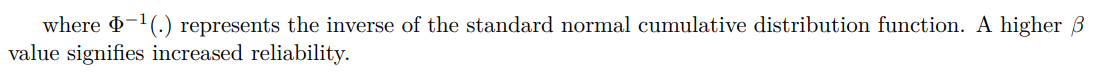
<ем>5.1.3. Ограничения и соображения

<ем>5.2. Общие настройки для моделирования системы репутации по методу Монте-Карло
В рамках сложных систем репутации, особенно тех, которые управляются такими механизмами, как «ставка кредитных баллов», задача заключается не только в построении надежной теоретической основы, но и в проверке ее жизнеспособности в различных сценариях реального мира. Здесь моделирование Монте-Карло выступает в качестве типичного инструмента, преодолевающего часто зияющую пропасть между теоретической надежностью и эмпирической эффективностью. Моделируя многочисленные раунды действий агентов, рейтингов и корректировок, мы можем получить представление о стабильности системы, распределении кредитных баллов и эффективности механизма ставок в продвижении желаемых действий.
Характер ставок, особенно с нетрадиционными показателями, такими как «кредитные баллы», привносит уровни изменчивости и потенциальных стратегических действий со стороны участников. Моделирование Монте-Карло с присущим ему стохастическим моделированием позволяет всесторонне исследовать эти действия в самых разных условиях. Запуская многочисленные симуляции, каждое из которых представляет возможное состояние мира, компания выявляет уязвимости, сильные стороны и непредвиденные последствия, связанные с системой.
Это систематическое исследование также устанавливает рейтинговую петлю. Результаты моделирования могут способствовать усовершенствованию базовой модели, гарантируя, что система репутации останется адаптивной и устойчивой. Например, если результаты моделирования покажут определенные стратегии, в которых производители могут чрезмерно централизовать ставки, теоретические конструкции можно скорректировать, чтобы сдержать такие действия, тем самым обеспечивая более справедливую и эффективную систему, если это то, на что нацелена модель.
Подчеркнем его значимость: метод Монте-Карло — это не просто инструмент тестирования. Это повторяющийся диалог между абстрактным миром теории и непредсказуемыми сферами практического применения. В контексте системы репутации, основанной на «ставках кредитных баллов», этот диалог имеет решающее значение, поскольку он укрепляет архитектуру модели в соответствии с требованиями реального мира и гарантирует ее долговечность и актуальность.
Результаты MCS будут проиллюстрированы и подробно обсуждены в разделах 5.5 и 5.6. Стоит отметить, что в результатах наших MCS наблюдались некоторые аномалии. Эти выбросы данных можно объяснить присущей методу моделирования случайностью и стохастическим характером. Метод Монте-Карло по своей конструкции использует случайную выборку для получения численных результатов для задач, которые в принципе могут быть детерминированными. Хотя закон больших чисел гарантирует, что эти симуляции сходятся к ожидаемому значению в течение огромного количества прогонов, случайные отклонения от ожидаемого результата не только возможны, но и ожидаемы из-за этой случайности. Детальное изучение этих аномалий дает представление о диапазоне возможных результатов, даже если они происходят с низкой вероятностью.
<ем>5.2.1. Разделение ставок между действиями и рейтингами

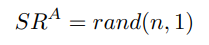

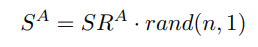
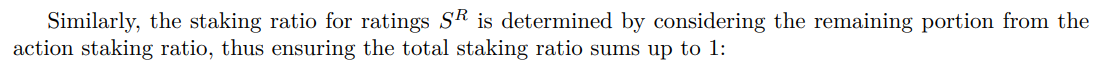

<ем>5.3. Сценарий первоначального равномерного распределения кредитных баллов между агентами
В контексте нашей теоретической модели системы репутации мы используем моделирование Монте-Карло для создания синтетических данных, которые соответствуют определенным статистическим свойствам. Для начальной MCS модели системы репутации мы предлагаем подход, при котором каждому агенту изначально предоставляется равная доля кредитных баллов. Агенты с соответствующим распределением кредитных баллов затем случайным образом определяют соотношение ставок для различных действий в системе. Основная цель этой схемы — выяснить, может ли такое равномерное распределение в сочетании со случайным подходом к ставкам стимулировать активное участие и способствовать позитивным действиям среди агентов.
Каждый агент Ai в системе, где i находится в диапазоне от 1 до n (общее количество агентов), начинает с одинаковой суммы кредита. баллы:

где CPtotal — общая сумма кредитных баллов в системе.


Благодаря единообразному начальному распределению кредитных баллов и случайным коэффициентам ставок основная цель системы — понять, склонны ли агенты к положительному участию. Ключевые моменты проверки включают в себя:
• Активное участие: с большей вероятностью будут ли агенты, имеющие равные права вначале, активно участвовать.
• Анализ рисков и вознаграждений: как агенты балансируют свои решения по ставкам, когда потенциальные вознаграждения и риски неопределенны.
• Динамика действий: если и как агенты корректируют свои коэффициенты ставок на основе наблюдаемых результатов, либо на основе их собственных действий, либо на основе действий других агентов.
Эта модель предлагает свежий взгляд на действия агентов, когда она представлена в системе репутации, которая начинается с равенства, а затем вводит случайность в решениях о ставках. Отслеживая действия агентов в этих условиях, мы можем получить представление об оптимальных стратегиях и корректировках, необходимых для создания среды более сотрудничества и взаимодействия.
<ем>5.4. Сценарий кредитных баллов, первоначально распределенных по степенному закону между агентами
Одной из фундаментальных проблем при разработке любой вычислительной модели является выбор правильных начальных условий и распределений, которые отражают сложность и нерегулярность реального мира. Эмпирические исследования в многочисленных областях, от экономики до природных явлений, часто демонстрируют, что некоторые системы не подчиняются простому равномерному распределению. Вместо этого они склоняются к распределениям, характеризующимся степенным законом.
Принцип Парето, в просторечии известный как правило 80-20, является ярким проявлением степенного закона распределения в социально-экономических условиях. Это предполагает, что примерно 80% последствий происходят от 20% причин, будь то распределение богатства, показатели продаж или другие явления. Этот принцип, основанный как на экономических рассуждениях, так и на математических обоснованиях, подчеркивает искаженную природу многих реальных распределений.
В свете этого, хотя начало с равномерного распределения обеспечивает чистую, симметричную основу для нашей модели, необходимо также изучить действие при распределении по степенному закону. Поступая так, мы можем обеспечить надежность нашей модели и ее способность обобщать реальные сценарии, где неравенство и дисбаланс часто являются нормой.
При случайной выборке MCS одной из основных проблем является генерация случайных чисел, которые придерживаются неравномерного распределения, такого как степенное распределение. Метод обратного преобразования предлагает элегантное решение этой проблемы [82, 83, 84, 85, 86].
<ем>5.4.1. Метод обратного преобразования
Метод обратного преобразования — это фундаментальный метод генерации случайных выборок из заданного распределения. Используя обратную функцию кумулятивного распределения (CDF), которая получается из функции плотности вероятности (PDF) для непрерывных переменных и функции массы вероятности (PMF) для дискретных переменных, этот метод может преобразовывать равномерно распределенные случайные числа, обычно из интервал (0, 1) на значения, соответствующие целевому распределению. Ссылаясь на формулу 9 CDF в разделе 3.4, мы разделяем применение этого метода на два сценария: непрерывный и дискретный.

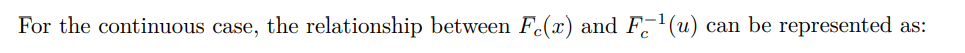

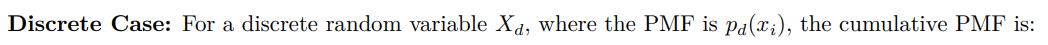
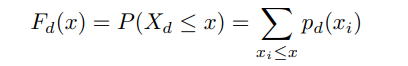

<ем>5.4.2. Применение метода обратного преобразования к степенным распределениям
Степенные законы, также известные как распределения Парето, часто возникают в различных природных и социальных явлениях. Для них характерны «тяжелые хвосты», указывающие на то, что хвостовые события (с низкой вероятностью) по-прежнему оказывают заметное влияние.
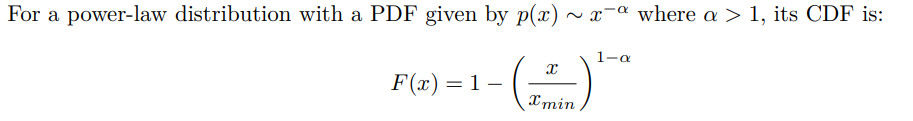
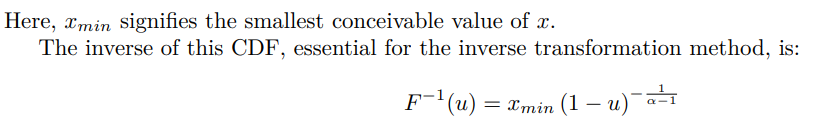
Метод обратного преобразования предпочтителен при моделировании систем со степенными характеристиками из-за:
• Его простая реализация, иллюстрируемая аналитической формой обратного CDF в уравнении (34).
• Его способность отражать уникальную природу тяжелого хвоста, присущую степенным распределениям.
Однако для распределений, в которых отсутствует определенный обратный CDF, этот метод может быть менее эффективным. Такие сценарии потребуют итеративных численных процедур, что потенциально увеличит вычислительные затраты и приведет к потенциальным неточностям.
В сумме метод обратного преобразования умело переводит равномерно распределенные случайные числа в числа, имеющие неравномерное распределение. В нашей модели системы репутации эта методология оказалась неоценимой для создания синтетических данных, которые отражают степенное распределение, подтверждая подлинность и точность модели.
<ем>5.5. Результаты и интерпретации моделирования Монте-Карло для базовой модели
После подготовки, описанной в разделе 5.2, мы без проблем выполнили MCS на базовой модели. Результаты полностью совпали с нашими ожиданиями, полученными в разделе 3.
<ем>5.5.1. Динамика кредитных баллов на основе действий агента
В нашей модели последствия действий агентов четко отражаются через выгоды или штрафы, которые они получают в виде кредитных баллов. Наши MCS категорически разделяют агентов на две основные категории на основе средних значений, присвоенных их действиям с меньшей дисперсией, чем у разных агентов, как это представлено в формуле 8 раздела 3.4.
<сильный>1. Выгодные участники: Агенты, наделенные более высокими средними значениями действий в симуляциях, неизменно получают положительную отдачу при оценке своих коллег. Величина их прироста кредитных баллов прямо пропорциональна сумме, которую они поставили во время своих действий, и сумме ставок оценивающих коллег.
<сильный>2. Вредные участники. И наоборот, агенты, которым присвоены более низкие средние значения действий, несут потери в кредитных баллах при оценке. Как и в случае с выгодоприобретателями, размер этих потерь напрямую зависит от суммы ставки агента во время его действий и доли оценивающих партнеров.
Чтобы проанализировать различия в уровнях действий среди агентов, мы используем переменную CDF, определенную в формуле 9 раздела 3.4. По мере развития моделирования различия в распределении кредитных баллов становятся более выраженными в зависимости от качества действий агентов. Это приводит к четкой тенденции: агенты, совершающие последовательные позитивные действия, получают больше выгод, а агенты, совершающие негативные действия, сталкиваются с возрастающими штрафами.
<ем>5.5.2. Связь между ставкой и вознаграждением в отношении рейтингов
Наши MCS, инициированные равномерным распределением кредитных баллов, проясняют сложную динамику между действиями агентов и прогрессивным распределением кредитных баллов. По ходу моделирования мы наблюдаем, что совокупная выгода или убыток, которые несет агент для каждого обзора, в первую очередь определяется двумя ключевыми факторами: знаком (положительным или отрицательным) его отзыва для конкретного агента и его соответствием или несоответствием большинству. консенсус. Кроме того, на величину этих выгод или убытков также пропорционально влияет сумма, которую агент обещает во время проверки, а также обещания, сделанные другими проверяющими. По сути, сумма ставки действует как множитель, усиливая потенциальную выгоду или ущерб. Таким образом, агенты будут испытывать различные совокупные выгоды или убытки с течением времени. Эти совокупные преимущества, или сумма индивидуальных рейтинговых результатов, зависят от таких факторов, как величина собственных ставок и ставок других оценщиков и особенно степень соответствия их рейтингов преобладающему мнению большинства.
В контексте степенного закона распределения наши выводы остаются поразительно схожими. Наши симуляции, инициализированные агентами, придерживающимися степенного закона распределения кредитных баллов, подчеркивают сложную взаимосвязь между действиями отдельных агентов и последующей динамикой распределения. Становится очевидным, что совокупная выгода или потеря агента от каждой оценки фундаментально определяется полярностью (положительной или отрицательной) его обратной связи для данного агента и ее соответствием или расхождением с консенсусом большинства. Совокупные выгоды, представляющие собой совокупность результатов отдельных рейтингов, зависят от различных факторов: частоты присвоения рейтингов агенту, суммы ставок, которые он делает во время своих оценок, и, главным образом, степени, в которой его отзывы отражают преобладающую точку зрения большинства.< /п>
<ем>5.6. Результаты и интерпретации моделирования Монте-Карло для продвинутых моделей
Крайне важно моделировать более продвинутые модели, которые очень похожи на реальные сценарии. Этот шаг необходим для всестороннего понимания динамики и последствий предлагаемой системы. Кроме того, перед официальным запуском системы репутации первостепенное значение имеет обширное тестирование в реальных условиях с реальными пользователями для обеспечения устойчивости и надежности системы. Это не только помогает выявить потенциальные проблемы, но также помогает усовершенствовать и оптимизировать модель для практического применения.
<ем>5.6.1. Адаптивная модель с обучением и корректировкой
На основе теоретического анализа, приведенного в разделе 4.2, мы видим заметную разницу между адаптивной моделью с обучением и адаптацией и моделями без обучения, касающимися ставок на действия. По ходу раунда агенты с положительной доходностью (часто признанные их коллегами) увеличивают свои ставки, увеличивая свои вознаграждения. И наоборот, агенты, получающие отрицательную доходность, главным образом из-за неблагоприятных рейтингов, уменьшают свою ставку, тем самым сокращая свои потери. Величина этих корректировок коррелирует с интенсивностью обучения (обозначается αL, как описано в разделе 4.3) и доходностью до тех пор, пока ставка не приближается к 0 или 1, после чего интервалы становятся незначительными.
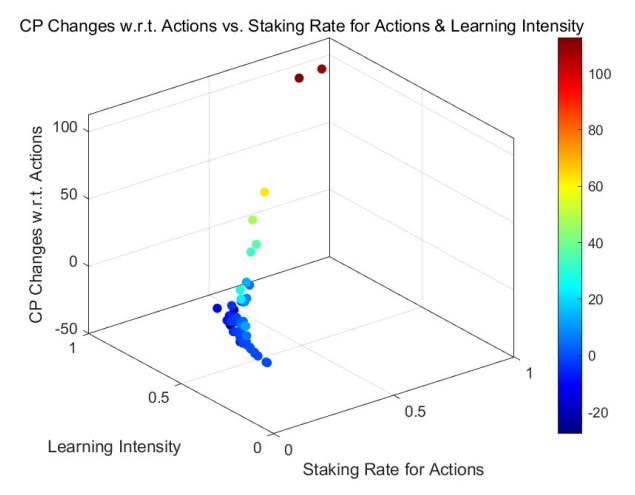
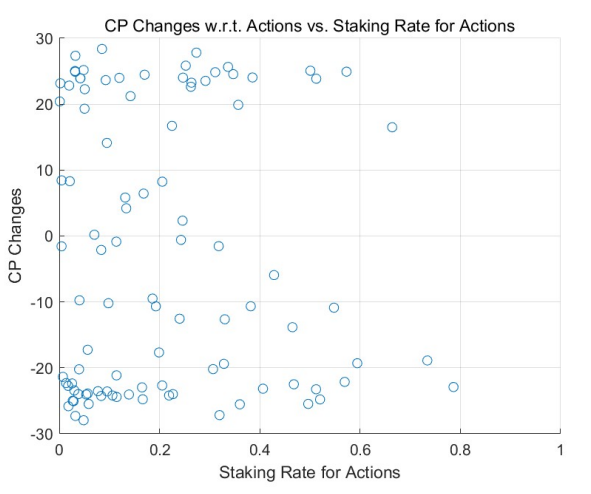
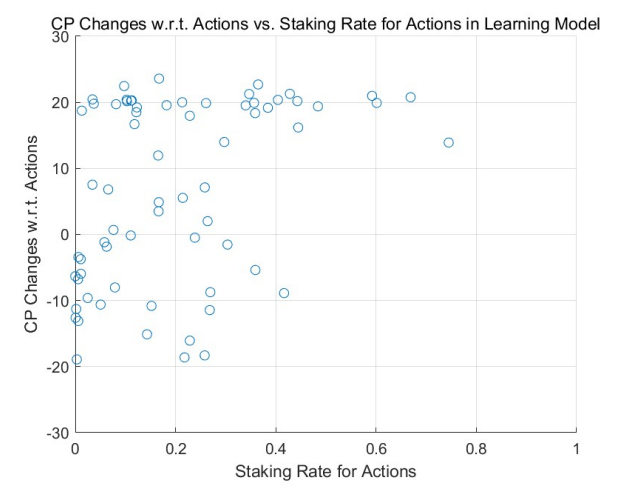
Такое поведение подтверждается результатами моделирования Монте-Карло (MCS), особенно в регионах с высокими ставками. Сравнительное исследование модели адаптивного обучения (см. рис. 3 для равномерного начального распределения и рис. 5 для степенного начального распределения) и модели без обучения (см. рис. 2 и рис. 4) подчеркивает эту тенденцию. Агенты с положительными результатами повышают свою ставку в high-stake
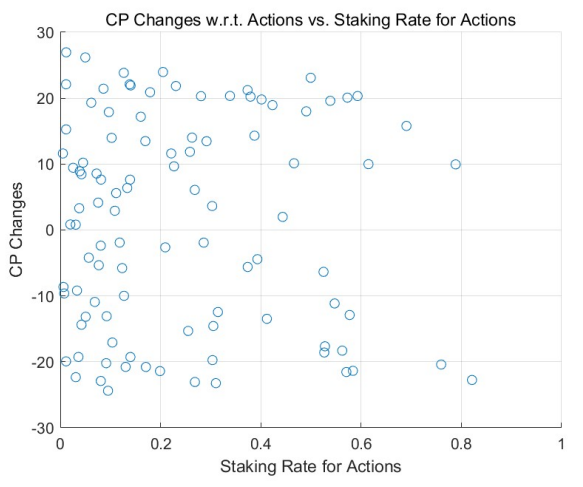
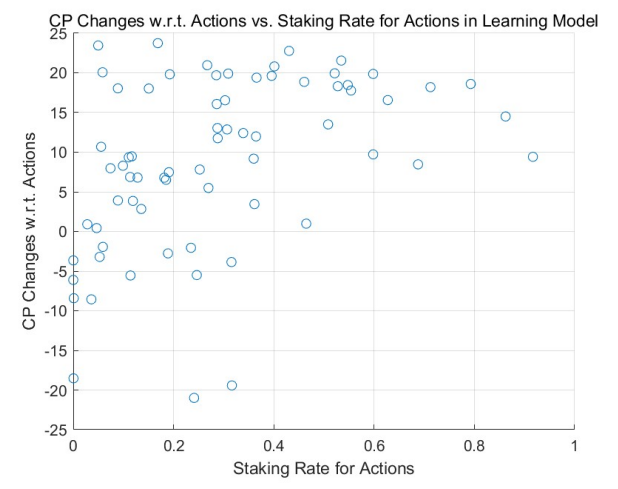
регионах, как видно из правых частей рисунков. Напротив, те, у кого отрицательные результаты, уменьшают свои ставки, тяготея к левой части диаграмм.
В течение нескольких раундов адаптивная модель с обучением и корректировкой демонстрирует рост числа агентов, достигающих положительной отдачи от действий с высокими ставками, тогда как модель без обучения показывает снижение числа таких агентов. Эта динамика напоминает естественную эволюцию свободных рынков, где специалисты преуспевают в своей области, повторяя поговорку: «Самые искусные люди справляются с самыми тонкими задачами».
В рамках модели обучения мы использовали моделирование Монте-Карло для оценки различной интенсивности обучения (обозначаемой αL) среди агентов, что подробно описано в разделе 4.3. Мы исследовали два сценария: равномерную интенсивность обучения для всех агентов и индивидуальную интенсивность.

Мы использовали два подхода к индивидуальной интенсивности обучения. Изначально мы присвоили случайные значения
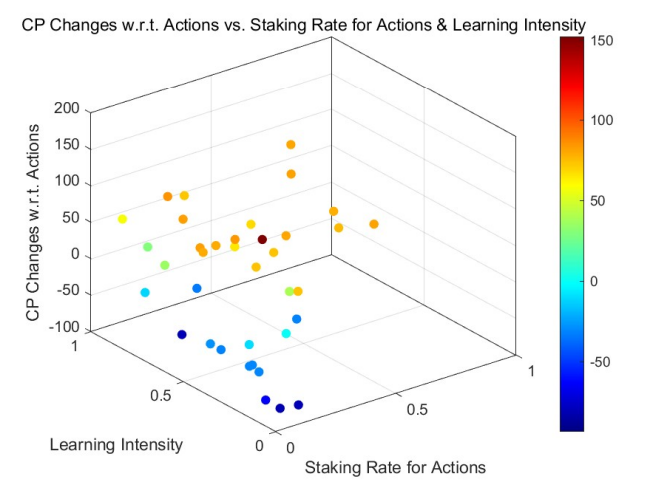


Для обоих подходов общие тенденции совпадают: агенты с более высокой интенсивностью обучения, как правило, получают больший кредитный выигрыш и меньшие потери. Под влиянием предыдущих результатов они корректируют свои ставки, оптимизируя баланс риска и прибыли.
Примечательно, что закономерности более выражены на рисунках 8 и 9, чем на рисунках 6 и 7. Это различие возникает из-за кумулятивного эффекта увеличения интенсивности ставок и обучения в течение раундов, что позволяет предположить, что изменения кредитов согласуются с этой интенсивностью с течением времени.< /п>
Более того, различия между начальными кредитными баллами, распределенными по равномерному и степенному закону, согласуются с нашими предыдущими обсуждениями. Роль интенсивности обучения в изменении кредитных баллов остается
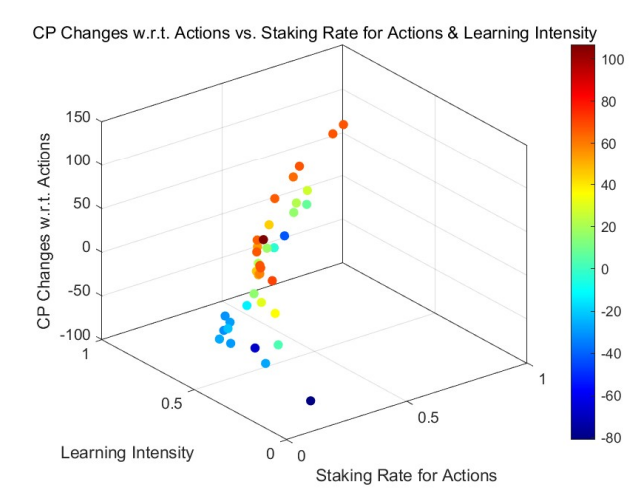
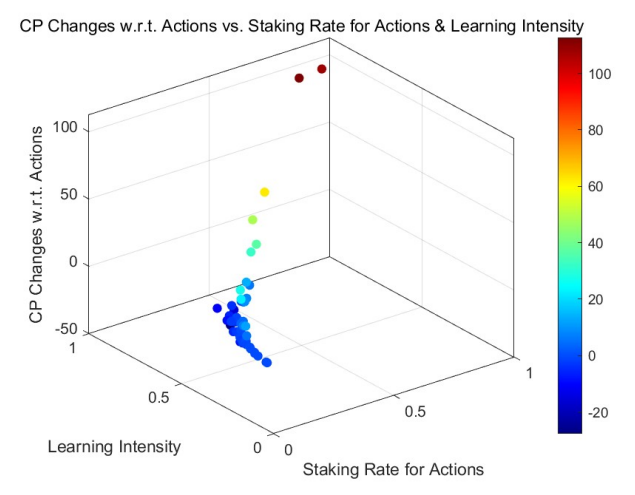
единообразен для различных начальных распределений, при этом степенное распределение сохраняет эффект длинного хвоста.
В отличие от ставок на действия, расхождение между адаптивными моделями и моделями без обучения, касающимися ставок на рейтинги, более тонкое. Этот нюанс возникает из-за сложности обучения на основе рейтинговых последствий. Агенты выигрывают, когда их рейтинги совпадают с рейтингами большинства, но сталкиваются с проблемами, когда они отличаются. Эта дисперсия несколько смягчает эффект «кейнсианского конкурса красоты» [87], когда агенты ожидают оценок большинства, а не предоставляют реальные оценки.
Эти результаты моделирования перекликаются с теоретическими положениями раздела 4.3. Они предполагают, что наша система репутации, ориентированная на блокчейн, эффективно создает внутрисетевой рыночный механизм, умело избегая проблем фальсифицированных рейтингов, распространенных на традиционных платформах сторонних поставщиков, как указано в разделе 1.
<ем>5.6.2. Разрешение агентам пропускать раунды
Мы разработали программу MCS, в которой реализован механизм, позволяющий агентам пропускать раунды. В частности, в каждом раунде определенная часть агентов не будет совершать никаких действий и давать какие-либо оценки. Если не указано иное, во всех последующих результатах моделирования будет учитываться этот механизм пропуска.
<ем>5.6.3. Моделирование неслучайного выбора потребителей
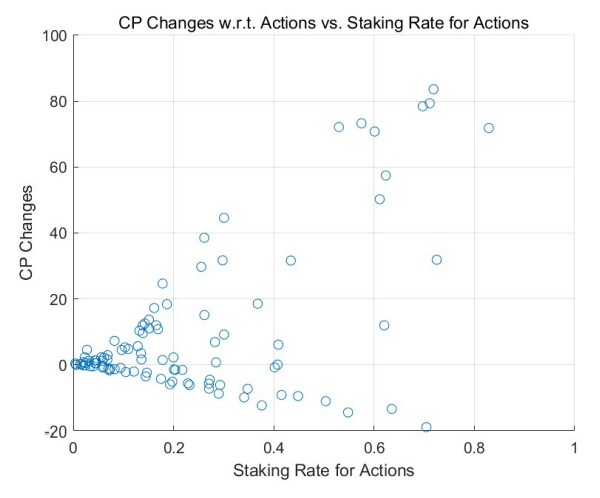
Как подробно описано в разделе 4.2, прозрачность информации о ставках естественным образом склоняет потребителей отдавать предпочтение производителям, которые поставили на ставку большее количество кредитных пунктов. Учитывая, что потребители по своей природе отдают предпочтение агентам-поставщикам с более высокой долей кредитных баллов, из этого следует, что те, у кого минимальные кредитные баллы ставятся за действия
с большей вероятностью будут упущены из виду и пропущены потребителями в соответствии с механизмом пропуска, описанным в Разделе 4.1 и Разделе 5.6.2. Теперь мы используем этот механизм пропуска для моделирования неслучайного выбора потребителей.
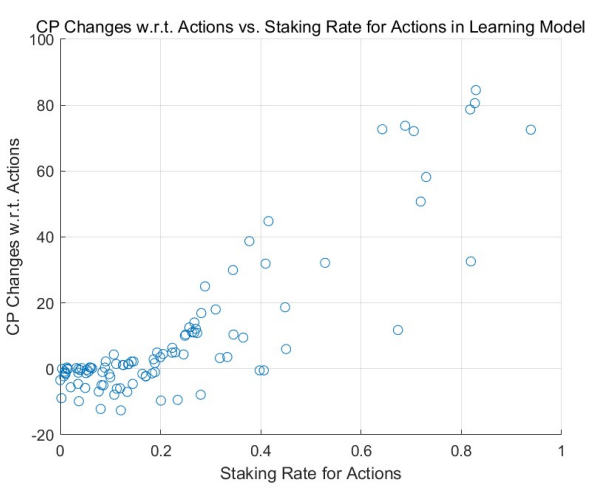
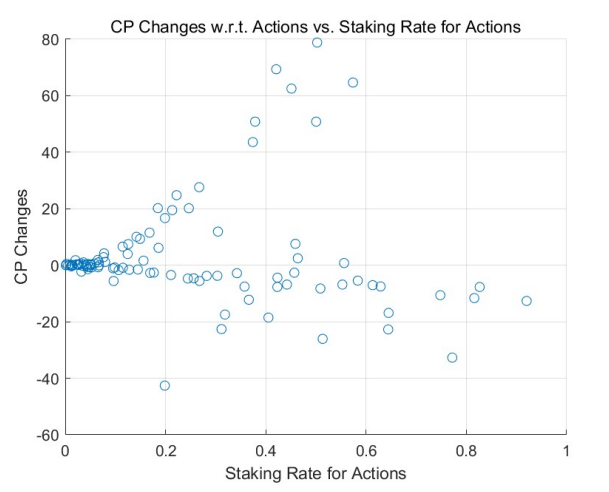
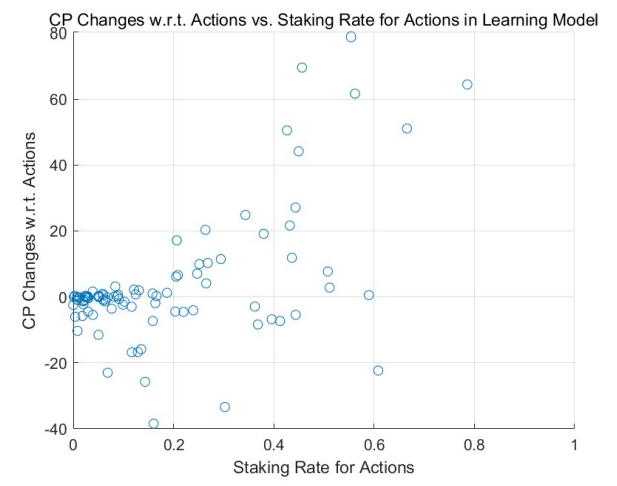
MCS проясняют динамику кредитных баллов относительно ставки ставок за действия, особенно когда включены механизмы отбора потребителей. Начиная с равномерного начального распределения, результаты для модели без обучения изображены на рисунке 10, а результаты модели обучения представлены на рисунке 11. Результаты, полученные из начального распределения по степенному закону, аналогичным образом показаны на рисунках 12 и 13. .
В ходе этих симуляций становится очевидной четкая тенденция: влияние механизмов отбора потребителей приводит к практически незначительной положительной или отрицательной отдаче для тех, кто ставит на действия минимальные кредитные баллы. Закономерности, наблюдаемые в регионах с высокими ставками (в правой половине рисунков), согласуются с предыдущими наблюдениями: агенты, получающие положительную доходность, склонны увеличивать свои ставки, тогда как те, кто получает отрицательную доходность, склонны снижать свои ставки, смещаясь в сторону более низких ставок. регионы ставок, т. е. левые части рисунков.
Это еще раз говорит о том, что задачи, как правило, чаще поручаются людям, которые ставят большее количество кредитных баллов за свои действия. С национальной экономической точки зрения можно сделать вывод, что эти агенты более склонны к совершению своих действий, возможно, из-за их специализированных навыков или по другим причинам. Следовательно, они часто получают положительные оценки. С другой стороны, те, кто менее специализирован или постоянно получает менее положительные отзывы, со временем оказываются маргинализованными. Эта развивающаяся ситуация перекликается с проверенным временем убеждением: «самые специализированные люди решают самые специализированные задачи».
<ем>5.6.4. Механизмы стимулирования вкладов
MCS с механизмами стимулирования вкладов указывают на то, что распределение кредитных баллов за действия и рейтинги вне системы может уменьшить кредитные баллы для других. Однако сетевой эффект, который обеспечивает конкурентные преимущества среди коллег, может повысить внутреннюю ценность каждого кредитного балла. Ожидается, что если механизм стимулирования будет разработан надлежащим образом, а это означает, что увеличение кредитных баллов перевешивает эффект разбавления, то в целом все в системе выиграют.
Оригинал

