Калибровка модели в машинном обучении: важная, но незаметная концепция

29 января 2023 г.

Содержание

• Введение
• Концепция калибровки модели
• Некоторые приложения для калибровки моделей в реальном времени
• Заключение
• Ссылки

Введение

Калибровка. Хотя это одна из самых важных концепций машинного обучения, о ней мало говорят начинающие энтузиасты в области искусственного интеллекта и машинного обучения. Калибровка говорит нам, насколько мы можем доверять предсказанию модели, особенно в моделях классификации. Хорошее понимание калибровки необходимо для осмысленной интерпретации числовых выходных данных классификаторов машинного обучения. В этой статье мы обсудим теорию калибровки модели машинного обучения и ее важность на нескольких простых примерах из реальной жизни.

Концепция калибровки модели

Модель машинного обучения считается откалиброванной, если она дает калиброванные вероятности. В частности, вероятности калибруются, когда предсказание класса с достоверностью p верно в 100*p процентах случаев

Выглядит сложно?

Давайте разберемся на простом примере:

Предположим, что нам нужно построить модель машинного обучения, чтобы предсказать, будет ли дождь в конкретный день или нет. Поскольку возможны только 2 исхода — «Дождь» и «Нет дождя», мы можем рассматривать это как модель бинарной классификации.

Здесь «Дождь» — это положительный класс, который представлен как 1, а «Нет дождя» — это отрицательный класс, который представлен как 0.

Если прогноз модели для определенного дня равен 1, то мы можем считать, что ожидается, что день будет дождливым.

Точно так же, если прогноз модели для определенного дня равен 0, мы можем считать, что ожидается, что день не будет дождливым.

В режиме реального времени модели машинного обучения часто представляют прогноз в виде числового вектора, представляющего некоторые значения вероятности.

Таким образом, нет необходимости, чтобы мы всегда получали значение 0 или 1. Обычно, если прогнозируемое значение больше или равно 0,5, оно считается 1, а если прогнозируемое значение меньше 0,5, то оно считается 0. .

Например, если прогноз модели на конкретный день равен 0,66, мы можем считать его равным 1. Точно так же, если прогноз модели на конкретный день равен 0,24, мы можем считать его равным 0.

Предположим, что наша модель предсказала результат на ближайшие 10 дней следующим образом:

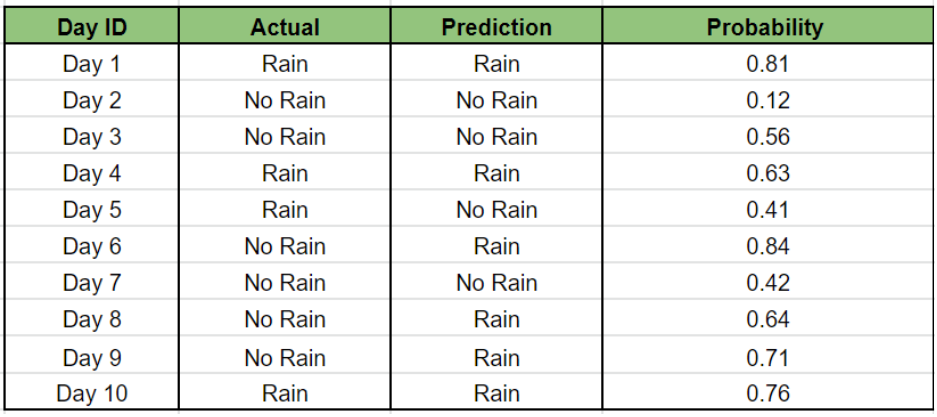
Мы видим, что если значение вероятности больше или равно 0,5, то прогноз «Дождь».

Аналогичным образом мы видим, что если значение вероятности меньше 0,5, то прогноз «Дождя нет».

Теперь вопрос статистики:

<цитата>

"Являются ли значения вероятности реальными значениями правдоподобия для результата?"

Другими словами, если у меня есть значение вероятности 0,8, означает ли это, что вероятность того, что день будет дождливым, составляет 80 %?

Если у меня есть значение вероятности 0,2, значит ли это, что существует 20% вероятность того, что день будет дождливым?

Статистически, если я утверждаю, что моя модель откалибрована, ответ должен быть «Да».

Значения вероятности не должны быть просто пороговыми значениями для определения класса выходных данных. Вместо этого он должен отражать реальную вероятность результата.

Здесь День 1 имеет значение вероятности 0,81, а День 10 имеет значение вероятности всего 0,76. Это означает, что, несмотря на вероятность дождя в оба дня, в 1-й день вероятность дождя на 5% выше, чем в 10-й. Это показывает силу вероятностного прогноза исхода. Хороший статистик выведет множество закономерностей из большого количества результатов, подобных этому, если у него есть такая модель.

Давайте посмотрим, как статистики интерпретируют калибровку модели графически.

Рассмотрите подобный график со значениями от 0 до 1, разделенными поровну по оси X-

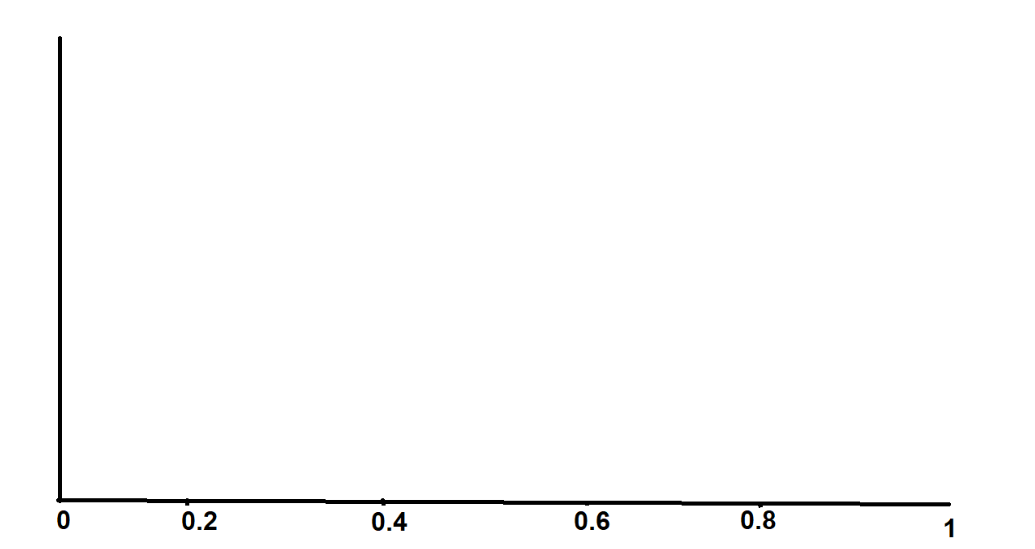
Теперь в каждом сегменте постройте график результатов в соответствии с их значениями вероятности.

Например,

В сегментах 0,6–0,8 у нас есть 4 точки данных: день 4, день 8, день 9 и день 10.

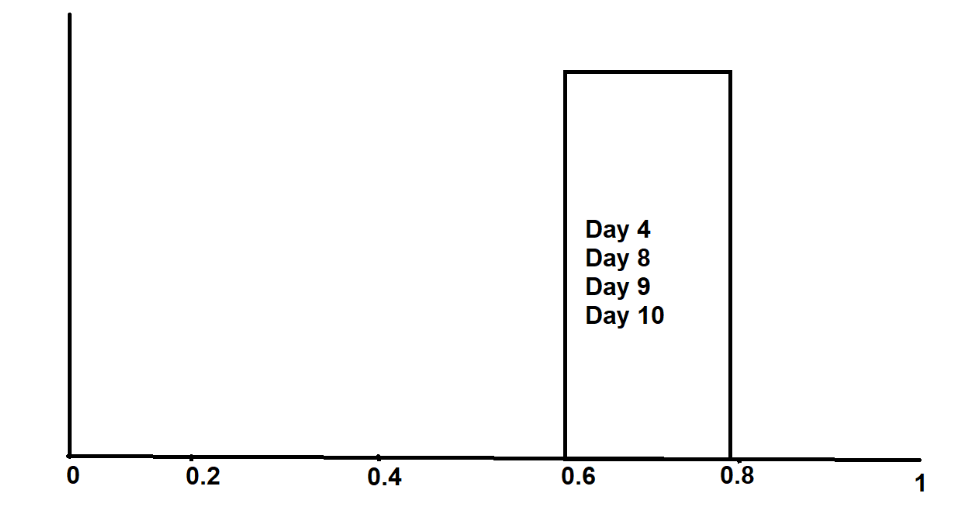
Точно так же мы можем выполнить ту же процедуру для всех других сегментов —

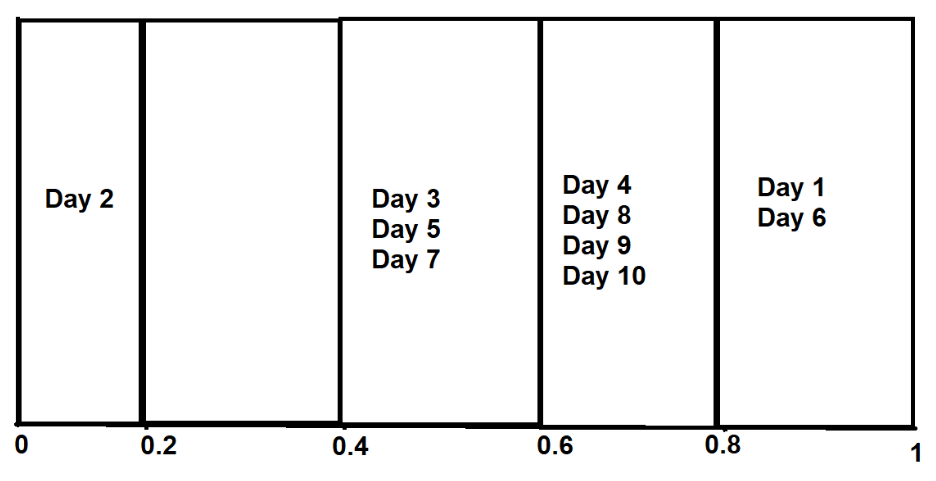До сих пор мы отображали только прогнозируемые значения.< /p>

Поскольку наш положительный класс — «Дождь», давайте продифференцируем значения в каждом ведре, фактическое значение которых — «Дождь». n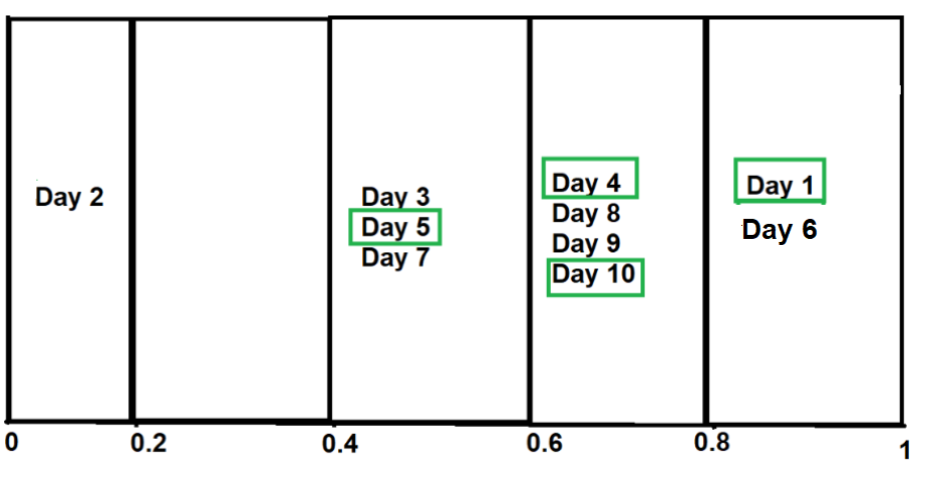

Теперь найдите долю положительного класса в каждом сегменте: n 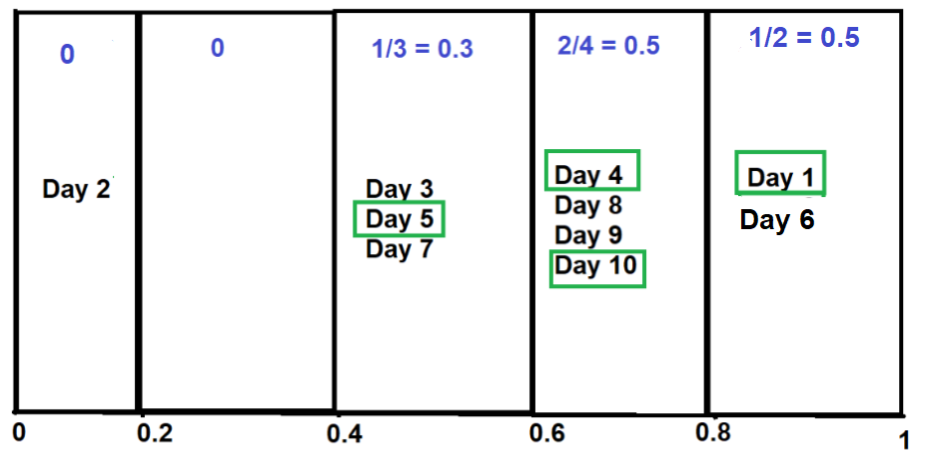< /p>

Как только этот этап будет достигнут, просто нанесите эти дробные значения в виде линии вдоль оси Y- n

Линия не имеет правильной линейной структуры. Это означает, что наша модель плохо откалибрована. График хорошо откалиброванной модели выглядел бы так:

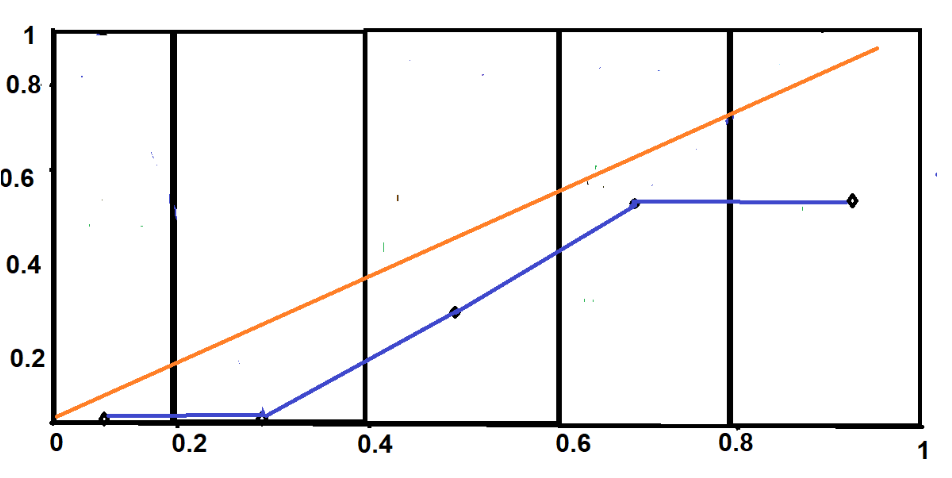
В идеале хорошо откалиброванная модель предполагает вероятность «Дождя» около 40%-60% в 3-м ведре (0,4-0,6). Однако наша модель дает только 30% вероятность того, что исход будет «Дождь». Это значительное отклонение. Подобные отклонения можно увидеть и в других сегментах.

Некоторые статистики используют площадь между калиброванной кривой и кривой вероятности модели для оценки эффективности модели. Когда площадь становится меньше, производительность будет выше, поскольку кривая модели будет ближе к калиброванной кривой.

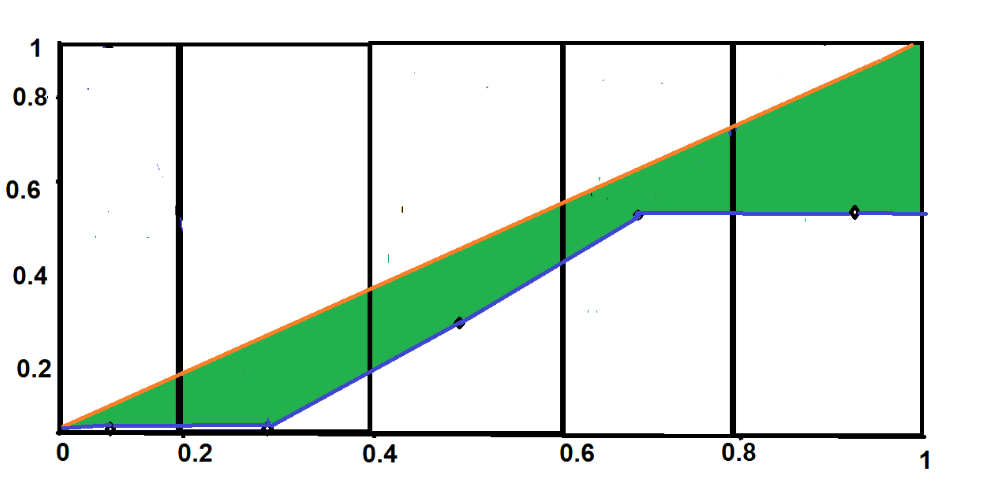
Некоторые приложения калибровки моделей в реальном времени для машинного обучения

Существует множество сценариев реального времени, в которых конечные пользователи приложений машинного обучения зависят от калибровки модели для эффективного и проницательного принятия решений, таких как-

1. Предположим, что мы создаем модель на основе ранжирования для платформы электронной коммерции. Если модель хорошо откалибрована, ее значениям вероятности можно доверять в качестве рекомендации. Например, модель говорит о том, что с вероятностью 80 % пользователю понравится продукт А и с вероятностью 65 %, что пользователю понравится продукт Б. Следовательно, мы можем рекомендовать пользователю продукт А в качестве первого предпочтения, а продукт Б в качестве второго предпочтения.

2. В случае клинических испытаний учтите, что некоторые врачи разрабатывают лекарства. Если модель предсказывает, что 2 препарата очень эффективны для лечения — препарат А и препарат Б. Теперь врачи должны выбрать наилучший доступный вариант из списка, поскольку они не могут рисковать, поскольку это очень рискованное испытание, связанное с человеческая жизнь. Если модель дает значение вероятности 95 % для лекарства A и 90 % для лекарства B, то врачи, очевидно, будут продолжать лечение лекарством A. n

Заключение

n В этой статье мы рассмотрели теоретические основы калибровки модели и обсудили важность понимания того, откалиброван классификатор или нет, на простых примерах из реальной жизни. Создание «надежности» для моделей машинного обучения часто является более сложной задачей для исследователей, чем ее разработка или развертывание на серверах. Калибровка модели чрезвычайно полезна в случаях, когда интерес представляет прогнозируемая вероятность. Это дает представление или понимание неопределенности в прогнозе модели и, в свою очередь, надежность модели, которую должен понять конечный пользователь, особенно в критически важных приложениях.

Я надеюсь, что эта статья помогла вам получить предисловие к этой концепции и понять ее важность. Вы можете обратиться к материалам, упомянутым в справочном разделе, чтобы получить более полное представление о них.

Ссылки

1. Калибровка — Википедия
2. Гебель, Мартин (2009 г.). Многомерная калибровка оценок классификатора в вероятностном пространстве (PDF) (кандидатская диссертация). Университет Дортмунда.
3. У. М. Гарчарек " Архивировано 23 ноября 2004 г. на Wayback Machine, "Правила классификации в стандартизированных пространствах разделов", диссертация, Дортмундский университет. , 2002 г.
<ли>. Хасти и Р. Тибширани, «Классификация попарным сцеплением». В: MI Jordan, MJ Kearns and SA Solla (ред.) , Достижения в системах обработки нейронной информации, том 10, Кембридж, MIT Press, 1998.

---

Оригинал