Интервалы слияния в алгоритмах Java (LeetCode)
20 октября 2022 г.Описание задачи:
По заданному массиву интервалов, где intervals[i] = [start_i, end_i], объединить все перекрывающиеся интервалы и вернуть массив не- перекрывающиеся интервалы, охватывающие каждый входной интервал.
Пример 1:
Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6].
Пример 2:
Input: intervals = [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considered overlapping.
Ограничения:
1 <= intervals.length <= 10^4интервалы[i].length == 20 <= начало <= конец <= 10^4
Обоснование:
Давайте попробуем сделать что-нибудь естественное. Нарисуем интервалы из первого примера. Это поможет нам понять природу проблемы и решить, какой подход следует использовать для ее решения.
У нас есть эти интервалы [1,3],[2,6],[8,10],[15,18]
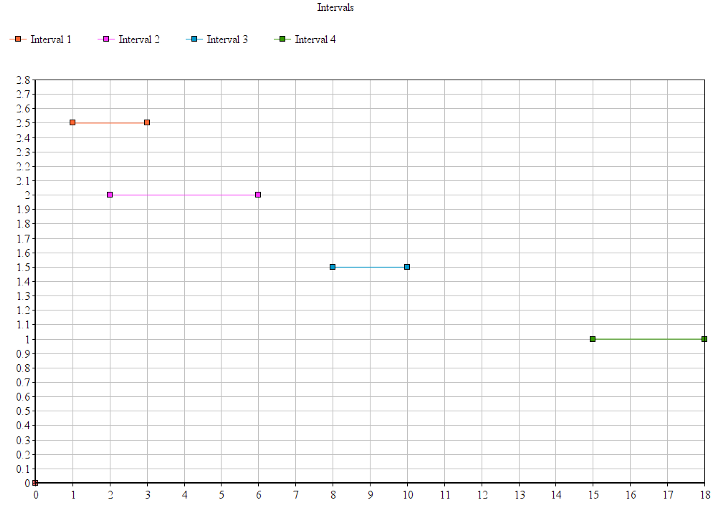
Глядя на эту диаграмму, мы можем сделать два важных наблюдения.
- Нарисовав линии, мы можем легко сказать, какие из них пересекаются.
- После того как мы рисуем линии, они сортируются.
Имея это в виду, мы можем продолжить решение.
Решение:
Первое, что мы хотим сделать, это отсортировать все имеющиеся у нас интервалы. Мы делаем это, чтобы объединить их вместе, когда смотрим на график выше. Это простая сортировка, мы начинаем с точки интервала, а затем с конца.
Arrays.sort(intervals, (a, b) ->
{
if (a[1] == b[1])
{
return a[0] - b[0];
}
return a[1] - b[1];
});
Как только интервалы отсортированы, мы можем начать их объединение. Глядя на график выше, мы можем сделать важное наблюдение — пересекающиеся интервалы перекрываются или начинаются в конечной позиции другого интервала. Мы будем использовать LinkedList, так как он предоставляет метод getLast(). Мы также можем использовать ArrayList и получить последний элемент, вызвав list.get(list.size() — 1). Для каждого интервала проверяем, есть ли у нас пересечение с предыдущим. Если у нас есть пересечение, мы просто объединяем их вместе и возвращаем в список.
LinkedList<int[]> list = new LinkedList<>();
for (int[] interval : intervals)
{
if (!list.isEmpty() && list.getLast()[1] >= interval[0])
{
while (!list.isEmpty() && list.getLast()[1] >= interval[0])
{
interval[0] = Math.min(list.getLast()[0], interval[0]);
interval[1] = Math.max(list.getLast()[1], interval[1]);
list.removeLast();
}
}
list.addLast(interval);
}
Последнее, что нужно сделать, это создать ответ. Мы делаем это, потому что изначально не знаем, сколько элементов не пересекаются друг с другом.
int pos = 0;
int[][] answer = new int[list.size()][];
for (int[] inteval : list)
{
answer[pos++] = inteval;
}
Решение задачи выглядит так:
public int[][] merge(int[][] intervals)
{
Arrays.sort(intervals, (a, b) ->
{
if (a[1] == b[1])
{
return a[0] - b[0];
}
return a[1] - b[1];
});
LinkedList<int[]> list = new LinkedList<>();
for (int[] interval : intervals)
{
if (!list.isEmpty() && list.getLast()[1] >= interval[0])
{
while (!list.isEmpty() && list.getLast()[1] >= interval[0])
{
interval[0] = Math.min(list.getLast()[0], interval[0]);
interval[1] = Math.max(list.getLast()[1], interval[1]);
list.removeLast();
}
}
list.addLast(interval);
}
int pos = 0;
int[][] answer = new int[list.size()][];
for (int[] inteval : list)
{
answer[pos++] = inteval;
}
return answer;
}
Приведенный выше код выглядит хорошо. Он имеет n log n временную и линейную пространственную сложность.

Также опубликовано здесь
Оригинал

