Машинное обучение: ваше полное руководство по выбору функций. Часть 2. Выбирайте самое лучшее

Введение

Добро пожаловать во вторую главу нашей серии статей о методах выбора функций в машинном обучении. В первой главе мы заложили основу, изучив фильтры методы, которые предлагают экономичный и эффективный подход к сокращению количества объектов в наборе данных. Теперь мы углубимся в мир выбора функций, сосредоточившись на двух других важных методах: методах-оболочках и встроенных методах.

Методы-оболочки

Они представляют собой более сложный и вычислительный подход по сравнению с методами фильтрации. Эти методы включают использование прогностических моделей для оценки подмножеств функций. , тем самым создавая более адаптированный и потенциально более эффективный набор функций для конкретной модели. В этой главе мы рассмотрим, как работают методы-оболочки, их преимущества и связанные с ними компромиссы, особенно с точки зрения вычислительных затрат и риска переобучения.

Встроенные методы

С другой стороны, он включает выбор функций в процесс построения модели. Эти методы присущи определенным алгоритмам, которые по своей сути выполняют выбор признаков при изучении параметров модели. Встроенные методы предлагают сбалансированный подход, сочетающий в себе сильные стороны методов фильтра и оболочки. Мы рассмотрим различные методы встроенных методов, обсудим, как они легко включают выбор признаков в процесс обучения модели и как они сравниваются с другими методами с точки зрения эффективности и результативности.

По мере изучения этой главы мы стремимся предоставить всестороннее понимание оболочек и встроенных методов, дополненное практическими примерами и идеями. Эти знания дадут вам возможность принимать обоснованные решения при выборе подходящего метода выбора функций для ваших проектов машинного обучения. Оставайтесь с нами, пока мы раскрываем сложности и нюансы этих продвинутых методов выбора функций.

Методы-оболочки

Суть этой категории методов заключается в том, что модель запускается на разных подмножествах признаков из исходного набора обучающих данных. Затем выбирается подмножество с лучшими параметрами на обучающем наборе, которое тестируется на тестовом наборе (тестовый набор не участвует в процессе выбора оптимального подмножества).

В этом классе методов есть два подхода:

• Прямой выбор
• Обратное исключение

Первый метод начинается с пустого подмножества, к которому постепенно добавляются различные функции (на каждом этапе выбирается оптимальное включение). Во втором случае он начинается с подмножества, равного исходному набору признаков, из которого они постепенно удаляются (каждый раз с перерасчетом классификатора).

Прямой выбор

• SequentialFeatureSelector (SFS) изначально запускается без функций и находит тот, который максимизирует оценку перекрестной проверки.
• После выбора первой функции SFS повторяет процесс, добавляя новую функцию к ранее выбранной.
• Процедура продолжается до тех пор, пока не будет достигнуто желаемое количество функций, определяемое параметром n_features_to_select. Если пользователь не указывает точное количество для выбора или порог улучшения качества, алгоритм автоматически выбирает половину существующего набора функций.

Ниже представлена ​​функция для процесса включения признаков на основе модели линейной регрессии OLS из библиотеки statsmodels, где критерием выбора признака будет полученный показатель статистической значимости (p-значение). от этой модели. Как и в первой главе, мы будем использовать набор данных Kaggle из «Титаника — машинное обучение на случай катастрофы» (https://www. kaggle.com/competitions/titanic/data):

from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.linear_model import LogisticRegression

LR = LogisticRegression()
sfs = SequentialFeatureSelector(LR, n_features_to_select=5)
sfs.fit(train, train_y)

sfs.get_support()

sfs.get_feature_names_out()

Выход:

Также в библиотеке mlxtend реализована функция SequentialFeatureSelector, которая принимает не только модель, но и тип метрики, по которой происходит включение, а также параметр front=True/False, отвечающий за для типа выбора, включения или исключения функций. (Подобный параметр существует в предыдущей функции SequentialFeatureSelector из sklearn, только он называется направлением и принимает значения «назад»/«вперед»):

from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.linear_model import LogisticRegression
# Sequential Forward Selection(sfs)
sfs = SFS(LogisticRegression(),
          k_features=11,
          forward=True,
          floating=False,
          scoring='accuracy',
          cv=0)

sfs.fit(train, train_y)
sfs.k_feature_names_

Выход:

Из всех продемонстрированных примеров мы получаем отфильтрованный список функций, который, по данным использованных моделей, невозможно улучшить по показателям качества за счет добавления остальных функций.

Обратное исключение

Тот же процесс, но в обратном направлении: начинается со всех функций, а затем начинается их удаление из набора.

Опять же, давайте рассмотрим специально написанную функцию, использующую модель OLS.

def backward_elimination(data, target,significance_level = 0.05):
    features = data.columns.tolist()
    while(len(features)>0):
        features_with_constant = sm.add_constant(data[features])
        p_values = sm.OLS(target, features_with_constant).fit().pvalues[1:]
        max_p_value = p_values.max()
        if(max_p_value >= significance_level):
            excluded_feature = p_values.idxmax()
            features.remove(excluded_feature)
        else:
            break 
    return features

# Example of usage
backward_elimination(train, train_y)

Выход:

Опять же функция SequentialFeatureSelector из sklearn, но с добавлением значения к параметру direction='backward' (стандарт значение параметра установлено на «переслать»).

from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.linear_model import LogisticRegression

LR = LogisticRegression()
sfs = SequentialFeatureSelector(LR, n_features_to_select=11,direction='backward')
sfs.fit(train, train_y)

sfs.get_support()

sfs.get_feature_names_out()

Выход:

#Sequential backward selection(sbs)
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
sbs = SFS(LogisticRegression(),
         k_features=11,
         forward=False,
         floating=False,
         cv=0)
sbs.fit(train, train_y)
sbs.k_feature_names_

Выход:

Как и в случае с включением функций, на выходе мы получаем список функций. Дальнейшее исключение любой функции из этого списка при обучении модели приведет к ухудшению метрики качества.

Сводка методов-оболочек

При изучении методов-оболочек ключевым аспектом, который следует учитывать, является их высокая вычислительная стоимость. И прямой выбор, и обратное исключение являются ресурсоемкими процессами, прежде всего потому, что они требуют многократного запуска модели для различных комбинаций признаков. Этот итерационный процесс, несмотря на его тщательность, требует значительных вычислительных мощностей, особенно для наборов данных с большим количеством функций.

Чтобы смягчить эти проблемы, можно использовать несколько стратегий:

1. Случайные перестановки. Вместо исчерпывающей оценки всех возможных комбинаций функций можно использовать случайные перестановки номеров функций для систематической оценки влияния добавления или исключения не только лучшей или худшей функции на каждом этапе. но также с учетом второго, третьего и т. д. Такой подход позволяет более тщательно изучить пространство признаков. Вот как мы можем это реализовать:

```питон из sklearn.model_selection импортировать cross_val_score импортировать numpy как np импортировать случайный

def Stepwise_random_permutation(модель, X, y, вперед=True, num_steps=5, num_permutations=30): лучший_score = 0 selected_features = установить() rest_features = set(X.columns)

   for step in range(num_steps):
       step_scores = []
       for _ in range(num_permutations):
           if forward:
               if not remaining_features:
                   break
               feature_to_add = random.sample(remaining_features, 1)[0]
               current_features = list(selected_features) + [feature_to_add]
           else:
               if not selected_features:
                   break
               feature_to_remove = random.sample(selected_features, 1)[0]
               current_features = list(selected_features - {feature_to_remove})

           score = cross_val_score(model, X[current_features], y, cv=5).mean()
           step_scores.append((score, feature_to_add if forward else feature_to_remove))

       if not step_scores:
           break

       step_scores.sort(reverse=True)
       best_feature = step_scores[0][1]
       if forward:
           selected_features.add(best_feature)
           remaining_features.remove(best_feature)
       else:
           selected_features.remove(best_feature)

       if step_scores[0][0] > best_score:
           best_score = step_scores[0][0]

   return selected_features, best_score

```

Эта функция будет итеративно добавлять или удалять функции в зависимости от их вклада в производительность модели, при этом не обязательно выбирая лучшую или худшую функцию на каждом этапе, а исследуя ряд основных функций для определения оптимальной комбинации.

2. Генетические алгоритмы. Эти алгоритмы имитируют процесс естественного отбора для выявления наиболее эффективных подмножеств признаков. Используя такие операции, как мутация, скрещивание и отбор, генетические алгоритмы могут эффективно перемещаться в пространстве поиска оптимальных или почти оптимальных решений. Этот метод обеспечивает баланс между исчерпывающим поиском и случайным выбором, потенциально сокращая время вычислений и одновременно выявляя сильные комбинации признаков.

Функция ниже использует подход генетического алгоритма для выбора признаков. Это более продвинутый метод, и для него могут потребоваться дополнительные библиотеки, такие как deap.

```питон из базы глубокого импорта, создателя, инструментов, алгоритмов импортировать numpy как np

def генетический_алгоритм_feature_selection(модель, X, y, n_gen=10, size_pop=50, prob_mut=0.2): Creator.create("FitnessMax", base.Fitness, Weights=(1.0,)) Creator.create("Индивидуальный", list, Fitness=creator.FitnessMax)

   toolbox = base.Toolbox()
   toolbox.register("attr_bool", random.randint, 0, 1)
   toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_bool, n=X.shape[1])
   toolbox.register("population", tools.initRepeat, list, toolbox.individual)

   def evalOneMax(individual):
       features = [i for i, x in enumerate(individual) if x == 1]
       if len(features) == 0: return 0,
       score = cross_val_score(model, X.iloc[:, features], y, cv=5).mean()
       return score,

   toolbox.register("evaluate", evalOneMax)
   toolbox.register("mate", tools.cxTwoPoint)
   toolbox.register("mutate", tools.mutFlipBit, indpb=prob_mut)
   toolbox.register("select", tools.selBest)

   pop = toolbox.population(n=size_pop)
   hof = tools.HallOfFame(1)
   stats = tools.Statistics(lambda ind: ind.fitness.values)
   stats.register("avg", np.mean)
   stats.register("min", np.min)
   stats.register("max", np.max)

   algorithms.eaSimple(pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=n_gen, stats=stats, halloffame=hof)

   return hof[0]

``` 3. Последовательные прогоны прямого/обратного исключения: На практике более осуществимым подходом часто является последовательное выполнение прямого или обратного исключения. Этот процесс включает добавление (или удаление) одной функции за раз в зависимости от ее влияния на производительность модели. Хотя этот метод не гарантирует абсолютно оптимальный набор функций, он имеет тенденцию определять высокоэффективное подмножество более вычислительно управляемым способом.

```питон из mlxtend.feature_selection импортировать SequentialFeatureSelector как SFS из клона импорта sklearn.base

def alternating_sequential_feature_selector(модель, X, y, итерации=5, оценка='точность', cv=5): current_features = установить() лучший_score = 0 best_features = Нет

   for i in range(iterations):
       forward = i % 2 == 0  # Alternate between forward and backward

       sfs = SFS(clone(model), 
                 k_features='best', 
                 forward=forward, 
                 scoring=scoring, 
                 cv=cv)

       sfs = sfs.fit(X[list(current_features) + list(X.columns.difference(current_features))], y)

       # Update current features and score
       new_features = set(X.columns[list(sfs.k_feature_idx_)])
       new_score = sfs.k_score_

       if new_score > best_score:
           best_features = new_features
           best_score = new_score

       current_features = new_features

   return best_features, best_score

```

В этой функции параметр iterations контролирует, сколько раз SFS запускается с переменными направлениями. модель клонируется на каждой итерации, чтобы гарантировать использование нового экземпляра для каждого запуска SFS. Эта функция попеременно добавляет функции (прямой выбор) и удаляет их (обратное исключение), стремясь итеративно уточнить набор функций.

Этот метод может привести к более тонкому процессу выбора функций, потенциально сбалансировав включение важных функций и удаление избыточных в ходе нескольких итераций.

Подводя итог, все эти подходы признают компромисс между вычислительными затратами и качеством выбранного набора функций. Применяя эти стратегии, становится возможным более эффективно использовать методы-оболочки даже для больших наборов данных, сохраняя при этом баланс между эффективностью вычислений и оптимальностью набора функций. В следующих разделах мы углубимся в практическое применение этих стратегий и рассмотрим, как их можно реализовать для улучшения процесса выбора функций в машинном обучении.

Встроенные методы

Наконец, встроенные методы позволяют не разделять выбор признаков и обучение модели, а выполнять выбор в процессе расчета модели. Эти методы требуют меньше вычислений, чем оболочки, но больше, чем фильтры.

Примеры встроенных методов:

• Регуляризация
• Ридж
• Лассо
• Важность функции
• На основе дерева
• RFE (исключение рекурсивных функций)
• Ценности Шепли

Регуляризация

Начнем с методов регуляризации. Существуют различные типы регуляризации, но основной принцип общий. Если рассматривать работу классификатора без регуляризации, то она предполагает построение модели, которая будет лучше всего подстраиваться под прогнозирование всех точек набора обучающих данных.

Например, если алгоритмом классификации является линейная регрессия, то выбираются коэффициенты полинома, аппроксимирующего зависимость между признаками и целевой переменной. Если оценкой качества выбранных коэффициентов служит среднеквадратическая ошибка, то параметры выбираются так, чтобы суммарный квадрат отклонений прогнозируемых классификатором точек от реальных был минимальным.

Идея регуляризации заключается в построении алгоритма, который минимизирует не только ошибку, но и количество используемых переменных.

В этом материале я лишь наглядно представлю формулы для типов задач с регуляризацией.



В процессе обучения алгоритма размеры коэффициентов будут пропорциональны важности соответствующих переменных, а перед теми переменными, которые меньше всего способствуют устранению ошибок, будут появляться близкие к нулю значения.

р>

Параметр регуляризации лямбда позволяет регулировать вклад оператора регуляризации в общую сумму. С его помощью можно задать приоритет — точность модели или минимальное количество используемых переменных.



Похоже на предыдущее во всем, кроме регуляризующего оператора. Это не сумма квадратов, а сумма абсолютных значений коэффициентов. Несмотря на небольшую разницу, свойства различаются. В Ridge по мере увеличения лямбды все коэффициенты получают значения, близкие к нулю, но обычно не становятся точно равными нулю. В Лассо с увеличением лямбды все больше коэффициентов становятся равными нулю и вообще перестают вносить вклад в модель. Таким образом, происходит фактический выбор признаков. Более значимые признаки сохранят свои коэффициенты ненулевыми, а менее значимые станут нулевыми.

Таким образом, регуляризация — это своего рода наказание за чрезмерную сложность модели, позволяющее защититься от переобучения при наличии избыточных функций.

В этом примере мы сразу запустим обе регрессии и получим коэффициенты (веса для каждого признака) из обученных моделей, а затем построим графики для визуализации значений этих коэффициентов.

# Ridge
clf = LogisticRegression(penalty='l2')
clf.fit(train, train_y)
coefs_ridge=pd.DataFrame(clf.coef_.T,index=train.columns, columns=['coef'])

# Lasso
clf = LogisticRegression(penalty='l1',solver='liblinear')
clf.fit(train, train_y)
coefs_lasso=pd.DataFrame(clf.coef_.T,index=train.columns, columns=['coef'])

fig, ax = plt.subplots(1, 2, figsize=(16, 8))
plt.rcParams.update({'font.size': 8})

sns.barplot(coefs_ridge.sort_values(
    'coef', ascending=False).reset_index(), x='coef', y='index', ax=ax[0])
ax[0].set_xlabel('Ridge Coef')
sns.barplot(coefs_lasso.sort_values(
    'coef', ascending=False).reset_index(), x='coef', y='index', ax=ax[1])
ax[1].set_xlabel('Lasso Coef')



Как мы видим, Регуляризация Лассо действительно обнулила большую часть функции. веса, поэтому мы можем уверенно использовать оставшиеся в качестве выбранных функций. В случае с регуляризацией Риджа мы также получаем четкую картину, с той лишь разницей, что нам нужно будет выбрать значение весов из модели в качестве порога для отсечения признаков.

Важность функции

Важность функции – это показатель, показывающий «важность» каждой функции для обучения конкретной модели. Более высокая важность означает, что конкретная функция будет иметь большее влияние на модель, используемую для прогнозирования конкретной целевой переменной.

Давайте возьмем реальный пример для лучшего понимания. Предположим, вам нужно купить новый дом рядом с вашим местом работы. При покупке дома вы можете учитывать различные факторы. Наиболее важным фактором при принятии решения может быть местоположение недвижимости, поэтому вы, скорее всего, будете искать дома, расположенные недалеко от вашего места работы. Важность функции работает аналогичным образом; он ранжирует функции на основе их влияния на прогнозы модели.

Древовидные модели

Важность функции рассчитывается как уменьшение количества необъяснимой информации в узле (точка ветвления, разделяющая лист дерева на два других листа), взвешенное по вероятности достижения этого узла. Вероятность узла можно рассчитать, разделив количество выборок, достигших узла, на общее количество выборок. Чем выше значение, тем важнее функция.

В математических определениях это можно описать следующими утверждениями.





Например, давайте рассмотрим обычный классификатор на основе деревьев решений (DecisionTreeClassifier) и получим значения важности признаков с помощью встроенной функции .feature_importances_ после обучения.< /п>

from sklearn.tree import DecisionTreeClassifier

model = DecisionTreeClassifier()
# fit the model
model.fit(train, train_y)
# get importance
importance = model.feature_importances_
fi_tree = pd.DataFrame(importance.T,index=train.columns, columns=['importance'])
plt.figure(dpi=100, figsize=(8, 8))
plt.rcParams.update({'font.size': 9})
plot_scores(fi_tree.importance, "Feature Importance")

Выход:



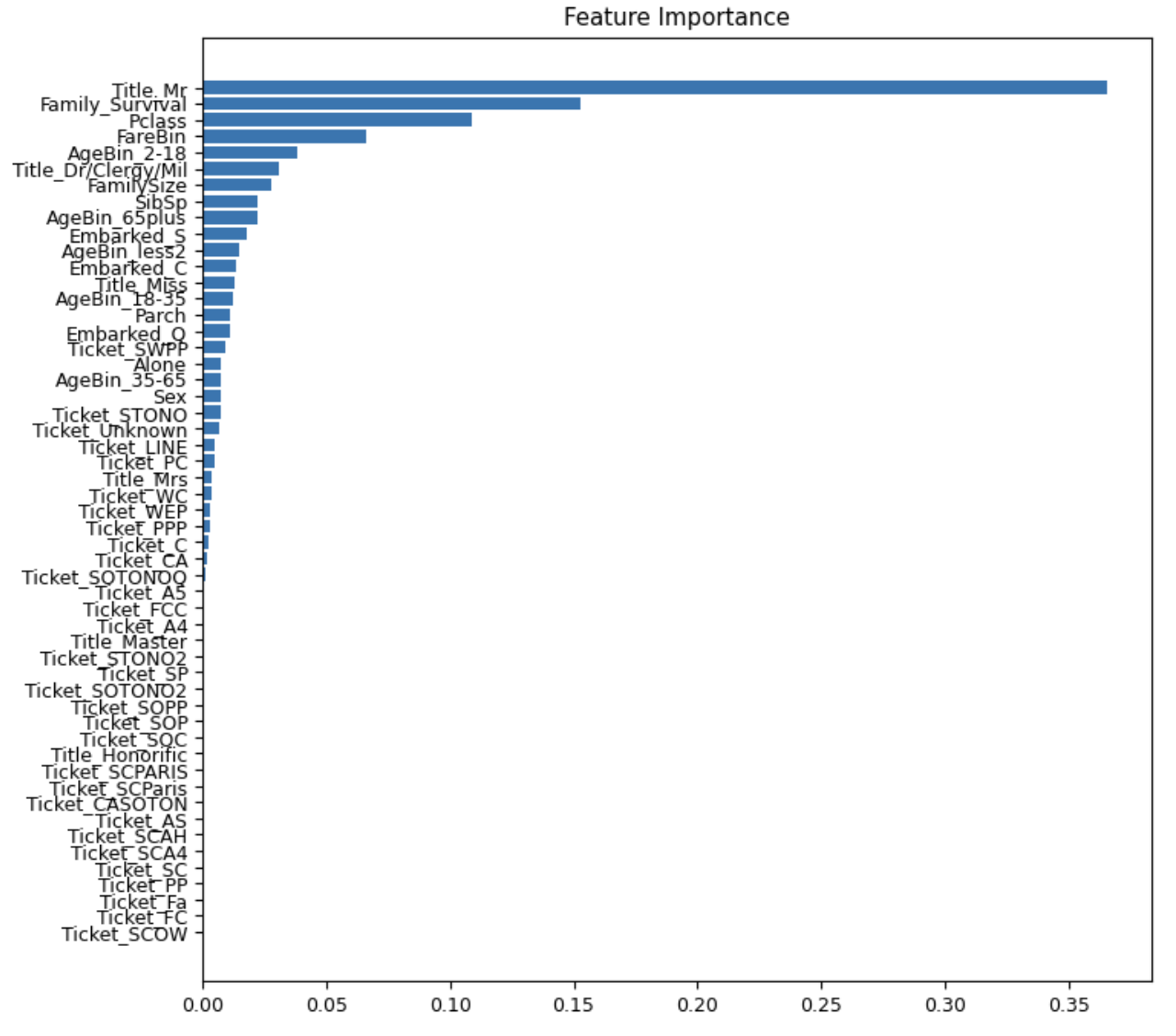
На графике мы можем наблюдать обычное распределение важности признаков; соответственно, чем выше важность функции, тем больше вероятность, что она будет работать лучше в будущей модели.

Рекурсивное исключение функций (RFE)

Одним из примеров таких методов является Recursive Feature Elimination (RFE). Как следует из названия, он принадлежит к классу алгоритмов, которые постепенно исключают функции из общего пула. Этот метод требует выбора классификатора, который будет использоваться для оценки признаков, например, линейной регрессии.

Например, изначально линейная регрессия обучается на всех признаках, и признак, получивший наибольшее значение абсолютного коэффициента во время обучения, откладывается. На следующем этапе обучение проводится по всем признакам, кроме отложенного, и так далее.

Хотя метод исключения лучше отслеживает взаимосвязи между объектами, он требует гораздо больше вычислительных затрат. Более того, все методы этой категории требуют значительно больше вычислений, чем методы фильтрации. Кроме того, в случае большого количества функций и небольшого размера набора обучающих данных эти методы подвержены риску переобучения.

Пошаговый процесс RFE:

1. Сначала RFE обучает пользовательскую модель всему набору функций. Пользовательской моделью может быть любая модель контролируемого обучения с методом fit_, который предоставляет информацию о важности функций.
2. Затем он вычисляет важность каждой функции обученной модели. Важность можно получить либо с помощью любого атрибута модели (например, coef_, feature_importances_), либо с помощью определяемой пользователем метрики.
3. Затем метод отбрасывает функцию с индикатором наименьшей важности и повторяет шаги 1 и 2 с уменьшенным количеством функций.
4. Шаг 3 повторяется до тех пор, пока количество функций не достигнет заданного пользователем значения.

Разница между RFE и SFS (последовательный выбор функций) заключается в том, что SFS не требует расчета показателей важности функций. SFS также может выполнять как прямой, так и обратный выбор, тогда как RFE может выполнять только обратное исключение. Более того, SFS обычно медленнее, чем RFE. Например, при обратном исключении переход от n признаков к n-1 с использованием k-кратной перекрестной проверки требует обучения n * k моделей, тогда как для RFE необходимо только k тренировок.

В качестве примера рассмотрим функцию RFE из библиотеки sklearn и введите в нее модель линейной регрессии ( RFE(LR,n_features_to_select=10) )

from sklearn.feature_selection import RFE

#select 5 the most informative features
rfe = RFE(LR,n_features_to_select=10) 
rfe = rfe.fit(train, train_y)
rfe.get_feature_names_out()

Выход:



В результате мы получим список функций (всего 10, поскольку мы сами установили этот порог), которые показали лучшие результаты за 10 итераций с точки зрения важности функций.

Значения Шепли (объяснения аддитивов Шепли)

Теория игр включает категорию кооперативных игр, в которых группы игроков могут объединять свои усилия, образуя коалиции для достижения наилучшего результата. В свою очередь, оптимальное распределение выигрыша между игроками можно определить с помощью вектора Шепли. Оно представляет собой распределение, в котором выигрыш каждого игрока равен его среднему вкладу в общее благосостояние при определенном механизме формирования коалиции (более строго из Википедии: ожидаемое значение их вклада в соответствующие коалиции):



Применяя приведенные выше принципы теории игр к интерпретации моделей ML, можно сделать следующие предположения:

• Результатом обучения с учителем (на основе приведенного примера) является игра;
• выигрыш — это разница между ожидаемым результатом на всех доступных примерах и результатом, полученным на данном примере;
• Вклад игроков в игру – это влияние каждого значения функции на выигрыш, то есть на результат.

Тогда при расчете вектора Шепли необходимо формировать коалиции из ограниченного набора признаков. Однако не каждая модель ML позволяет просто удалить функцию без переобучения модели с нуля. Поэтому для формирования коалиций признаки обычно не удаляются, а заменяются случайными значениями из «фонового» набора данных. Усредненный результат модели со случайными значениями признака эквивалентен результату модели, в которой этот признак полностью отсутствует.

Практическая реализация этого подхода представлена ​​специальной библиотекой SHAP (Shapley Additive exPlanations), которая поддерживается для моделей «ансамблей деревьев» в XGBoost, LightGBM, CatBoost, scikit-learn и pyspark.

Например, мы обучаем модель xgboost и используем библиотеку Shap для иллюстрации распределения значений вектора Шепли.

import shap
import xgboost as xgb
from sklearn.model_selection import train_test_split

model_xgb = xgb.XGBClassifier(
    base_score=0.5, booster='gbtree', colsample_bylevel=1,
       colsample_bynode=1, colsample_bytree=1, gamma=0, learning_rate=0.1,
       max_delta_step=0, max_depth=3, min_child_weight=1, missing=None,
       n_estimators=100, n_jobs=1, nthread=None,
       objective='binary:logistic', random_state=0, reg_alpha=0,
       reg_lambda=1, scale_pos_weight=1, seed=None, silent=None,
       subsample=1, verbosity=1)

model_xgb.fit(train, train_y)


shap_values = shap.TreeExplainer(model_xgb).shap_values(train)
shap.summary_plot(shap_values, train, show=True, color_bar=True)

Выход:



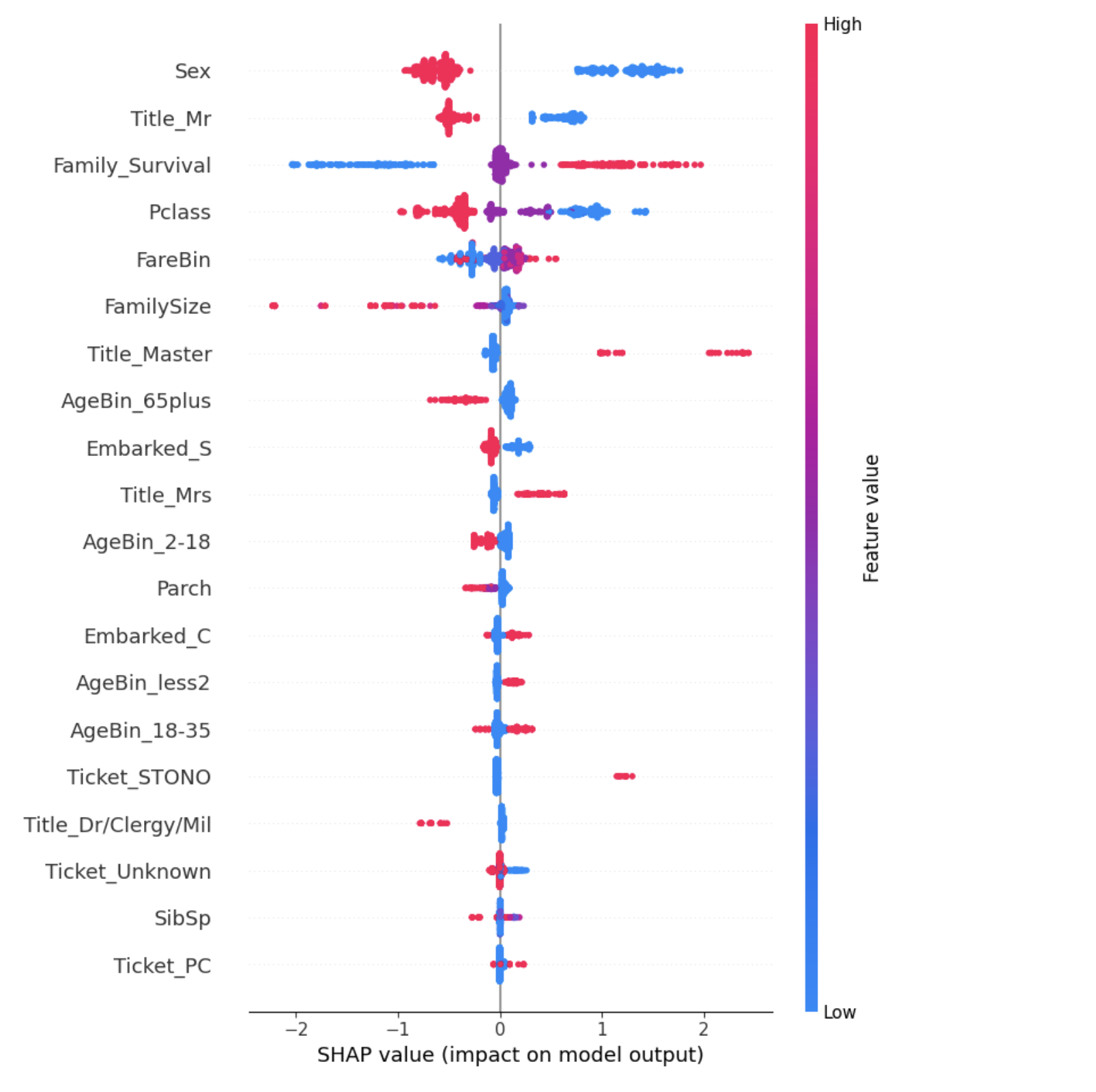
Полученный график интерпретируется следующим образом:

• значения слева от центральной вертикальной линии представляют отрицательный класс (0), а справа — положительный (1) в соответствии с матрицей ошибок модели прогнозного машинного обучения (чем дальше влево, тем больше модель стремится уверенно отнести наблюдение к классу 0 и, наоборот, чем дальше вправо - к классу 1)
• толщина линии прямо пропорциональна количеству точек наблюдения;
• чем краснее точки, тем выше значение функции в этой точке.

Например: В наших данных переменная Пол принимает два значения {"мужской": 1, "женский": 0} На рисунке мы видим, что значительная часть (которая довольно велика, учитывая толщину линия) значений 1 (краснее — большее значение) расположены слева от вертикальной линии, то есть данный признак влияет на модель следующим образом: модель с высокой степенью достоверности классифицирует мужчин как не выживших, а женщин — как выживших (целевая переменная Survived - 1/0, где 1 означает выживший)

Другой возможный метод использования — вычисление среднего значения Шепли:

explainer = shap.Explainer(model_xgb, train)
shap_values2 = explainer(train)
shap.plots.bar(shap_values2)



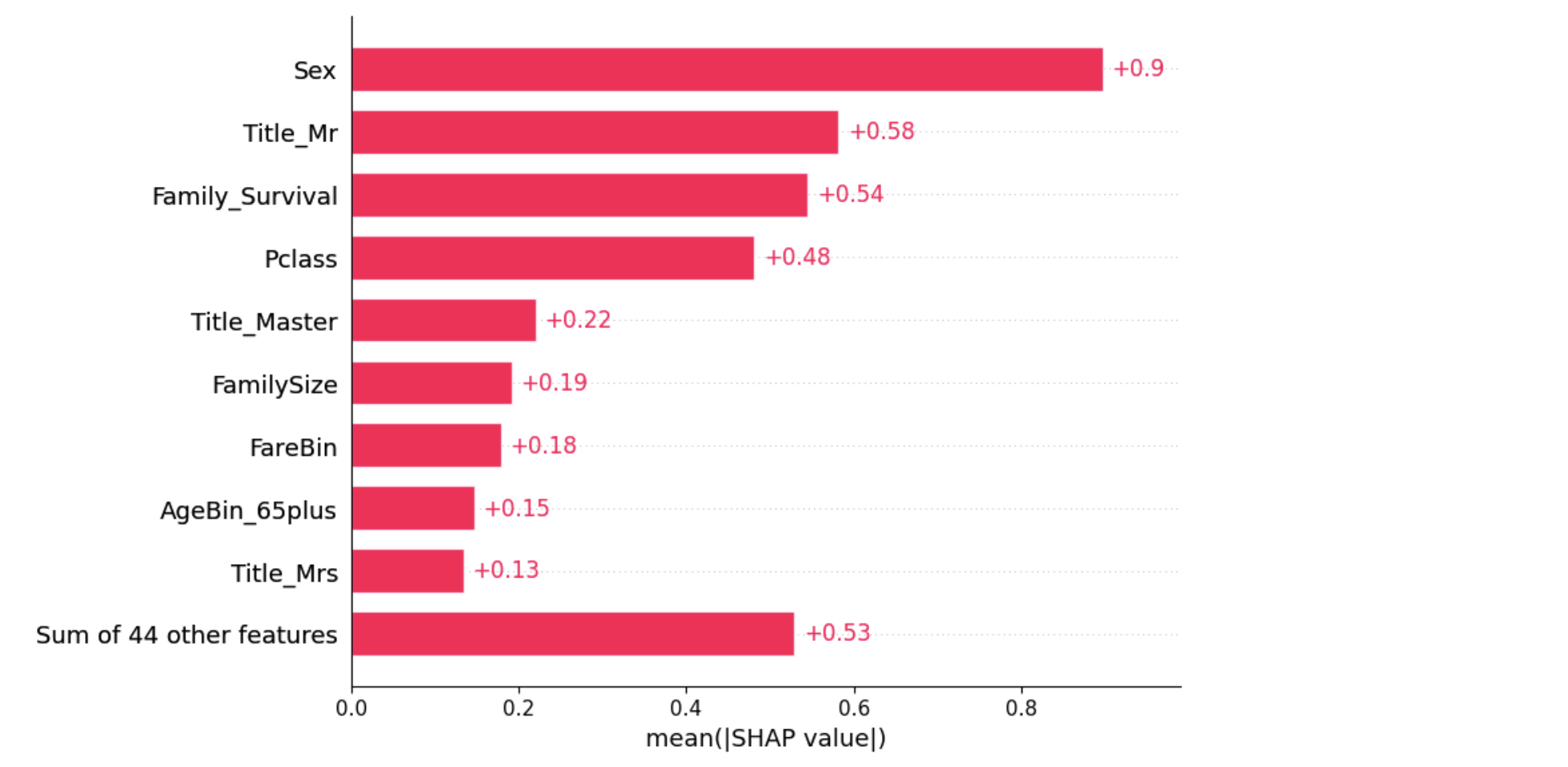
Этот график позволяет нам посмотреть средние абсолютные значения Шепли для каждого признака, которые можно интерпретировать так же, как важность признака.

Заключение

Завершая вторую часть нашей серии статей о методах выбора функций в машинном обучении, мы рассмотрели тонкости оболочек и встроенных методов. Наше путешествие началось с углубленного изучения методов-оболочек, которые, хотя и требуют больших вычислительных ресурсов, предлагают индивидуальный процесс выбора, потенциально повышая производительность модели. Затем мы перешли к использованию встроенных методов, которые элегантно интегрируют выбор функций в процесс обучения модели, обеспечивая гармонию между эффективностью и результативностью.

На протяжении всей этой главы мы вооружились практическими идеями и примерами, которые освещают сильные стороны и потенциальные недостатки каждого метода. От тщательной оркестровки функций в методах-оболочках до встроенных возможностей выбора встроенных методов — теперь у нас есть более четкое представление о выборе правильной техники для наших проектов.

Оставайтесь с нами до следующей главы, в которой мы раскроем тайну роли AutoML в выборе функций, предоставив путь к эффективному построению моделей и предоставив нам возможность использовать весь потенциал наших данных. Присоединяйтесь к нам, и мы шагнем в будущее машинного обучения, где выбор функций становится не искусством, а наукой, и все это благодаря достижениям AutoML.

---

Оригинал