Машинное обучение: ваше полное руководство по выбору функций. Часть 1. Фильтруйте самое интересное

Основная идея и подходы сериала

Выбор признаков, также известный как выбор переменных, выбор атрибутов или выбор предикторов (реже обобщение), представляет собой тип абстракции, процесс выбора подмножества значимых признаков (как зависимых, так и независимых переменных) для построения модели.

Выбор функций используется по четырем причинам:

• Упрощение модели для повышения интерпретируемости
• Чтобы сократить время обучения.
• Чтобы избежать проклятия размерности
• Чтобы улучшить способность модели к обобщению и бороться с переобучением.

Проклятие размерности — проблема, связанная с экспоненциальным увеличением объёма данных из-за увеличения размерности пространства. Это приводит к следующим трудностям:

• Вычислительная трудоемкость.
• Необходимость хранить огромный объем данных.
• Увеличение доли шума
• В линейных классификаторах увеличение числа признаков приводит к проблемам мультиколлинеарности и переобучения.
• В метрических классификаторах расстояния обычно рассчитываются как средний модуль различий по всем признакам. Согласно Закону больших чисел, сумма n слагаемых стремится к определенному фиксированному пределу при n → ∞. Таким образом, расстояния во всех парах объектов имеют тенденцию иметь одинаковое значение и, следовательно, становятся неинформативными.

Основная идея использования метода выбора признаков заключается в том, что данные содержат определенные признаки, и если некоторые из них являются избыточными или незначительными, их можно удалить без существенной потери информации. «Избыточный» и «незначительный» — это два разных понятия, поскольку одна значимая особенность может быть избыточной при наличии другой значимой особенности, с которой она сильно коррелирует.

Методы выбора признаков обычно делятся на три класса в зависимости от того, как они сочетают алгоритмы выбора и построение модели.

• Методы фильтрации
• Методы-оболочки
• Встроенные методы

Далее мы обсудим немного теории о каждом из этих методов, а затем рассмотрим более конкретные примеры для каждого из них.

Методы фильтрации (Методы фильтрации)

Эти методы используют косвенный индикатор вместо показателя ошибки для оценки подмножества функций. Этот показатель выбран таким образом, чтобы его можно было легко рассчитать, сохраняя при этом полезность набора функций. Обычно применяемые показатели включают взаимную информацию, коэффициент корреляции смешанных моментов Пирсона, расстояние между классами или внутри них или результаты критериев значимости для каждой комбинации класса/функции.

Фильтрация обычно требует меньше вычислительных затрат, чем упаковка, но в то же время фильтрация дает наборы функций, которые не настроены на определенный тип прогнозной модели. Этот недостаток означает, что набор признаков, полученный в результате фильтрации, является более общим, чем набор, полученный с помощью методов-оболочек, и совершенно не связан с будущими моделями, что приводит к более низкой способности модели к обобщению, чем при использовании методов-оболочек, поскольку признаки выбираются без участия каких-либо модели. Однако набор признаков, полученный после фильтрации, не содержит предположений о прогнозной модели и, следовательно, больше подходит для обнаружения связей между признаками.

Многие методы фильтрации обеспечивают ранжирование признаков, но не дают явно лучшего подмножества, а точка отсечения в рейтинге выбирается с помощью перекрестной проверки.

Методы фильтрации также используются в качестве этапов предварительной обработки для методов-оболочек, что позволяет применять фильтрацию к более крупным задачам. Методы фильтрации очень эффективны по времени при вычислениях и устойчивы к переобучению.

Методы-обертки (Методы-обертки)

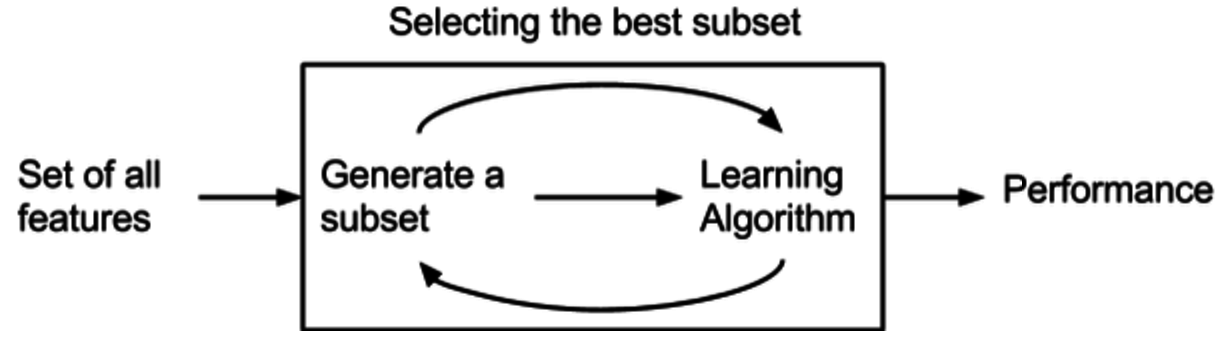
Методы-оболочки для выбора функций используют модель предварительной оценки производительности для ранжирования подмножеств функций. Каждое новое подмножество используется для обучения модели, которая затем тестируется на контрольной выборке. Метрика, рассчитанная на этой контрольной выборке, дает оценку для данного подмножества.

Два основных недостатка этих методов:

• Повышенный риск переобучения при недостаточном количестве наблюдений.
• Значительное время вычислений при большом количестве переменных.

Поскольку методы-оболочки включают перебор всех подмножеств функций с последующим обучением модели, они являются наиболее затратными в вычислительном отношении, но обычно дают лучший набор функций для конкретной модели.

Встроенные методы (Встроенные методы)

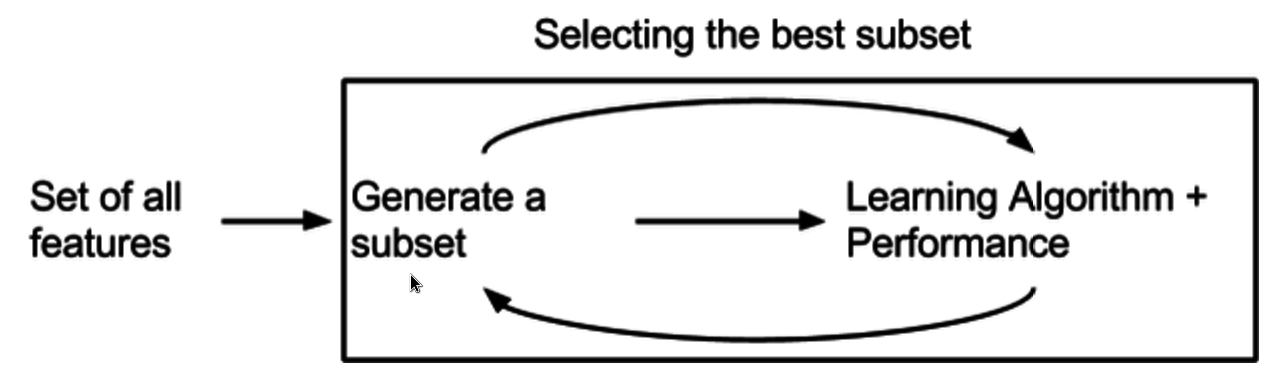
Встроенные методы — это обобщающая группа методов, выполняющих выбор признаков в процессе построения модели. Алгоритм обучения имеет преимущество собственного процесса выбора переменных и одновременно выполняет выбор и классификацию признаков. Позже мы обсудим этот метод более подробно на примерах.

В будущем для отработки примеров кода будет использован экспериментальный набор данных, взятый из чрезвычайно популярной задачи бинарной классификации для прогнозирования выживших на Титанике (https://www.kaggle.com/competitions/titanic/data).

Методы фильтрации

Методы фильтрации основаны на статистических методах и обычно рассматривают каждую функцию независимо. Они позволяют оценить и ранжировать признаки по значимости, под которой понимается степень их корреляции с целевой переменной. Давайте рассмотрим несколько примеров.

Взаимная информация

Метод тесно связан с понятием информационной энтропии. Формула энтропии довольно проста:

Чтобы лучше понять смысл этой меры, можно рассмотреть два простых примера. Во-первых, подбрасывание монеты, при котором вероятность выпадения орла и решки равна. В этом случае энтропия, рассчитанная по формуле, будет равна 1. Однако если монета всегда выпадает решкой вверх, то энтропия будет равна 0. Другими словами, энтропия, близкая к 1, указывает на равномерное распределение, а близкая к 0 указывает на что-то интереснее.

Чтобы рассчитать корреляцию между переменными, нам нужно определить еще несколько показателей. Первым из них является частичная условная энтропия:

Условная энтропия рассчитывается как:

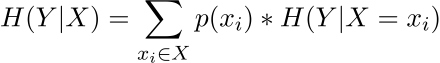
Интересна не сама мера, а ее отличие от обычной энтропии признака Y. Это мера того, насколько более упорядоченной для нас становится переменная Y, если мы знаем значения X. Или, проще говоря, есть ли корреляция между значениями X и Y и насколько она сильна. На это указывает значение - взаимная информация (взаимная информация):

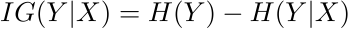
Чем больше параметр IG, тем сильнее корреляция. Таким образом, мы можем легко рассчитать показатель взаимной информации для всех признаков и удалить те, которые слабо влияют на целевую переменную. Тем самым, во-первых, сокращается время расчета модели, а во-вторых, снижается риск переобучения.

Итак, чтобы проверить это, мы напишем нашу собственную функцию make_mi_scores, используя mutual_info_classif из библиотеки sklearn, которая вычисляет оценку взаимной информации для функции, а также добавляет функцию plot_scores для отображения взаимной информации.

from sklearn.feature_selection import mutual_info_classif

def make_mi_scores(X, y, discrete_features):
    mi_scores = mutual_info_classif(X, y, discrete_features=discrete_features)
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
    mi_scores = mi_scores.sort_values(ascending=False)
    return mi_scores

mi_scores = make_mi_scores(train, train_y, discrete_features='auto')
mi_scores[::3]  # show a few features with their MI scores


def plot_scores(scores,name):
    scores = scores.sort_values(ascending=True)
    width = np.arange(len(scores))
    ticks = list(scores.index)
    plt.barh(width, scores)
    plt.yticks(width, ticks)
    plt.title(name)


plt.figure(dpi=100, figsize=(8, 8))
plt.rcParams.update({'font.size': 9})
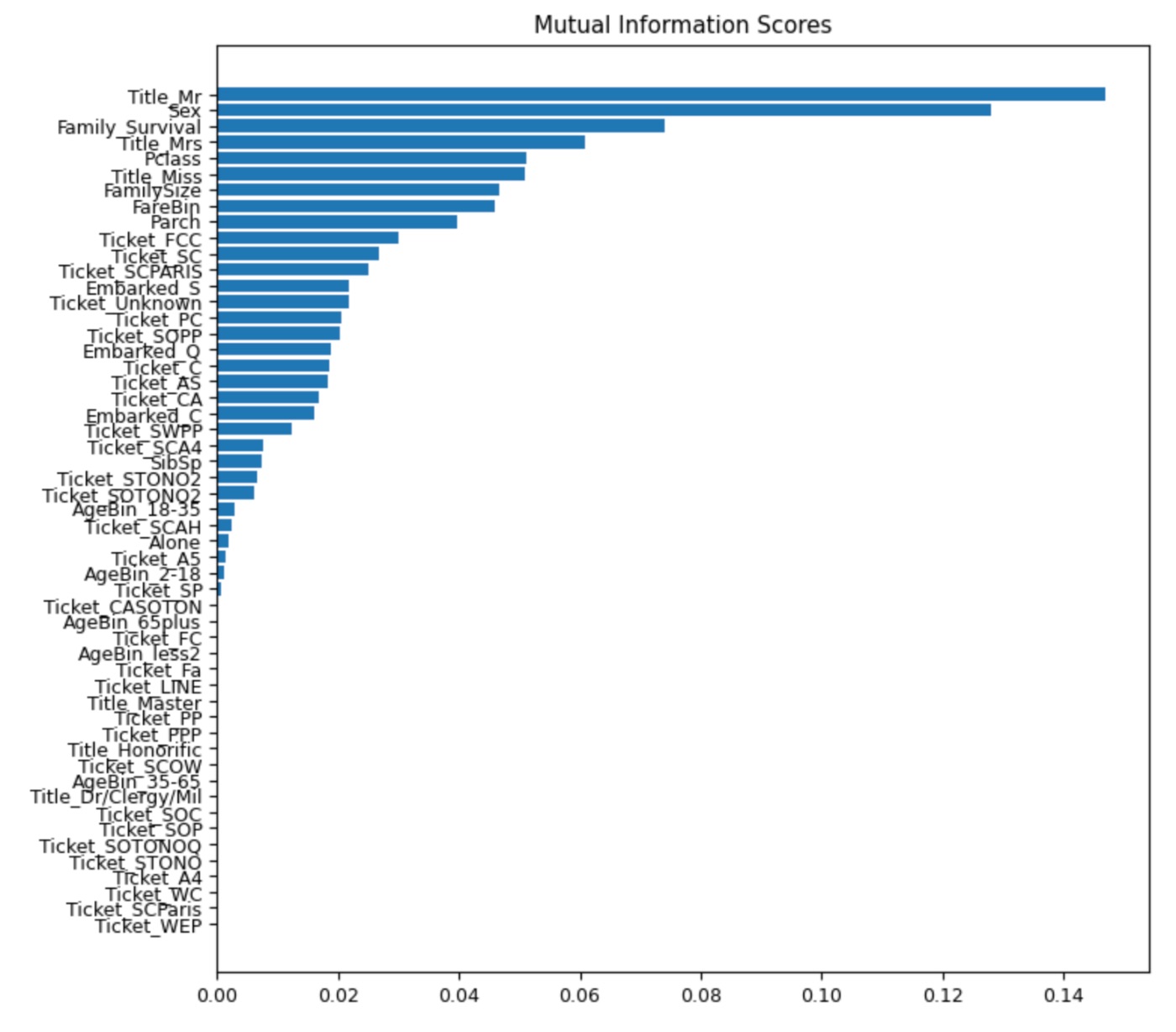
plot_scores(mi_scores, "Mutual Information Scores")

И вывод:

Корреляция Пирсона

Коэффициент корреляции Пирсона характеризует наличие линейной зависимости между двумя величинами.

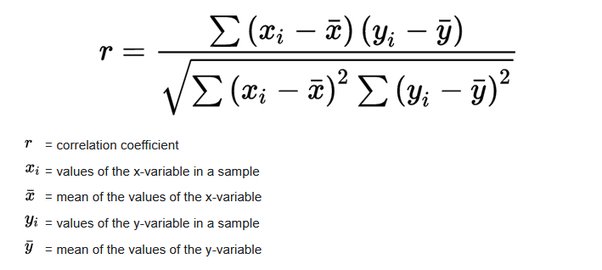
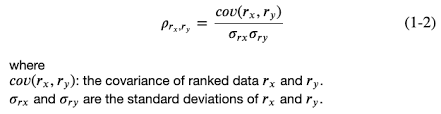
Коэффициент корреляции Пирсона можно использовать для определения силы линейной связи между величинами (другие типы связей выявляются с помощью методов регрессионного анализа).

Необходимо понять разницу между понятиями «независимость» и «некоррелированность». Первое подразумевает второе, но не наоборот. Например, корреляция между возрастом и ростом у детей вполне очевидна в причинно-следственном отношении, а вот корреляция между настроением и здоровьем людей менее очевидна. к улучшению здоровья, или хорошее здоровье приводит к хорошему настроению, или и то, и другое? Или есть другой фактор, лежащий в основе обоих? Другими словами, корреляция может рассматриваться как свидетельство возможной причинно-следственной связи, но не может указывать на то, какой может быть причинно-следственная связь если он есть.

Корреляция обычно рассчитывается:

1. Между каждой функцией и целевой переменной для определения важности каждой функции в описании поведения целевой переменной.
2. Попарно между всеми объектами, чтобы определить схожие объекты в пространстве.

Коэффициент Пирсона относится к числу параметрических статистических критериев. Это означает, что его можно использовать только в том случае, если параметры, которые мы коррелируем, удовлетворяют определенным условиям, главным из которых является нормальность распределения.

Итак, пример кода будет выглядеть так:

train_pearson_corr_with_target = (
    train.corrwith(train_y["Survived"], method="pearson")
    .to_frame()
    .rename(columns={0: "corr"})
    .join(
        train.corrwith(train_y["Survived"], method="pearson")
        .to_frame()
        .abs()
        .rename(columns={0: "abs_corr"})
    )
).sort_values("abs_corr",ascending=False)
train_pearson_corr_with_target.head()

plt.figure(dpi=100, figsize=(8, 8))
plt.rcParams.update({'font.size': 8})
plot_scores(train_pearson_corr_with_target.abs_corr,'Pearson Correlation')

Выход:





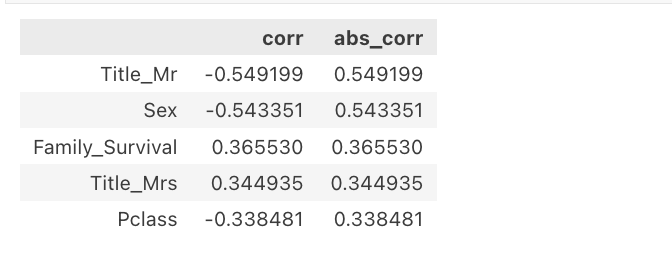
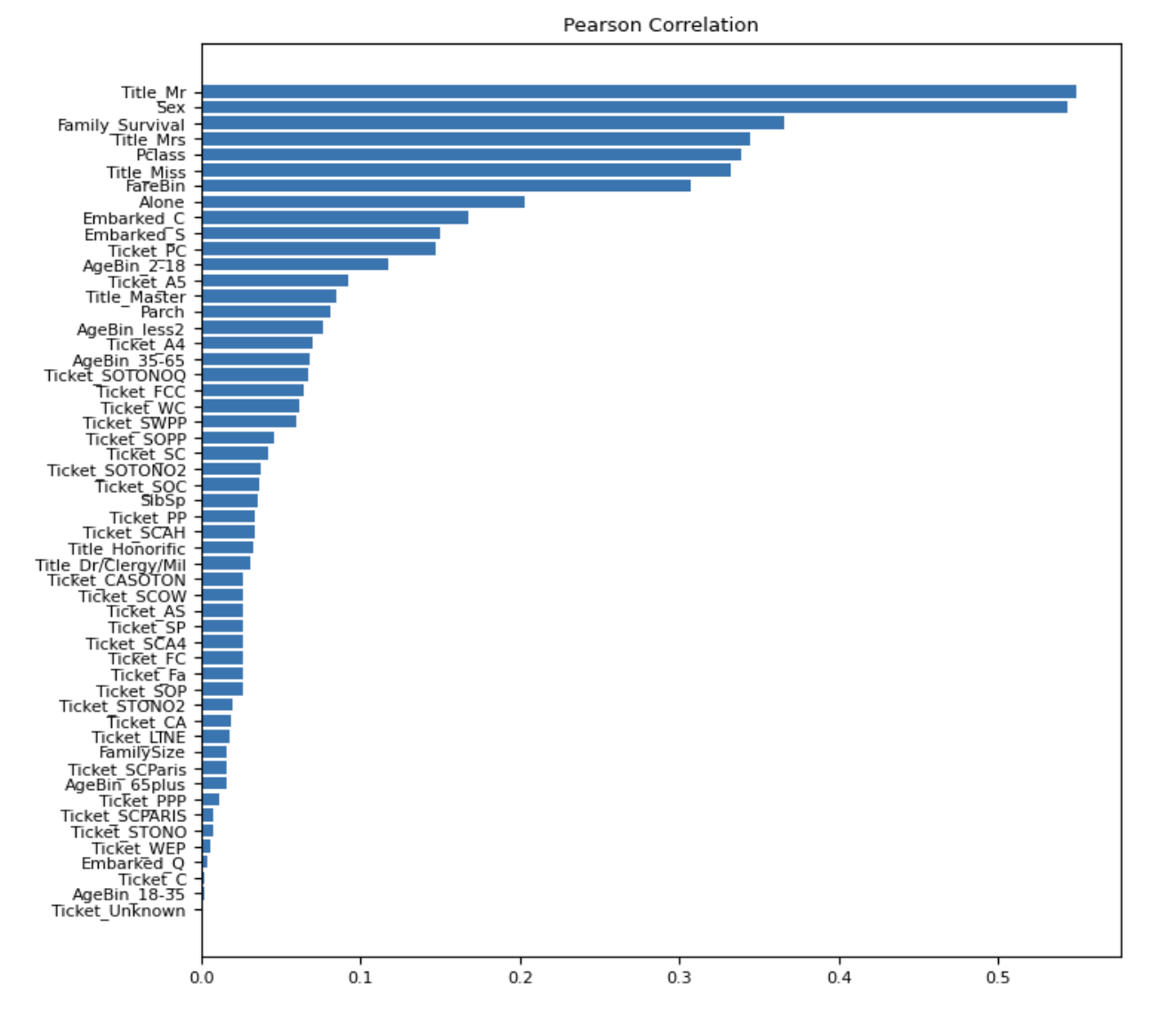
На графике выше мы можем наблюдать распределение значений корреляции с целевой переменной по различным функциям.

Примечательно, что объекты с высокими показателями взаимной информации также имеют высокие коэффициенты корреляции Пирсона.

Корреляция Спирмена

Коэффициент корреляции Спирмена — это мера линейной связи между случайными величинами. Корреляция Спирмена основана на рангах, то есть вместо числовых значений для оценки корреляции используются соответствующие ранги. Рангом наблюдения в данном случае является его порядковый номер в вариационном ряду, т. е. вместо фактических значений признака используется номер в последовательности значений признака, расположенных в неубывающем порядке. Другими словами, порядковый номер после сортировки по возрастанию.



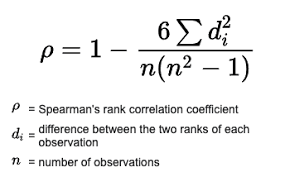
Коэффициент инвариантен к любому монотонному преобразованию шкалы измерения. Следовательно, параметры, между которыми рассчитывается корреляция, не обязательно должны иметь нормальное распределение.

Данные часто не имеют нормального распределения, и в этом случае, строго говоря, коэффициент Пирсона использовать нельзя. В таких случаях следует использовать коэффициенты Спирмена.

Таким образом, метод Спирмена более универсален и менее строг, чем метод Пирсона. Точность Пирсона немного выше, но в контексте задач машинного обучения это не принципиально.

Итак, пример кода будет выглядеть точно так же, как пример Пирсона:

train_spearman_corr_with_target = (
    train.corrwith(train_y["Survived"], method="spearman")
    .to_frame()
    .rename(columns={0: "corr"})
    .join(
        train.corrwith(train_y["Survived"], method="spearman")
        .to_frame()
        .abs()
        .rename(columns={0: "abs_corr"})
    )
).sort_values("abs_corr",ascending=False)
train_spearman_corr_with_target.head()

plt.figure(dpi=100, figsize=(8, 8))
plt.rcParams.update({'font.size': 8})
plot_scores(train_pearson_corr_with_target.abs_corr,'Pearson Correlation')

Выход:





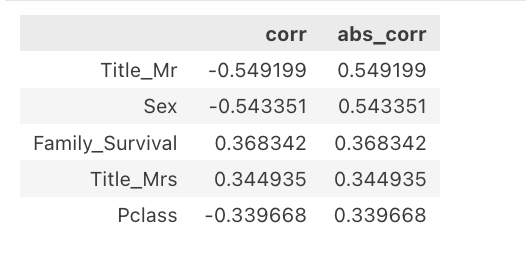
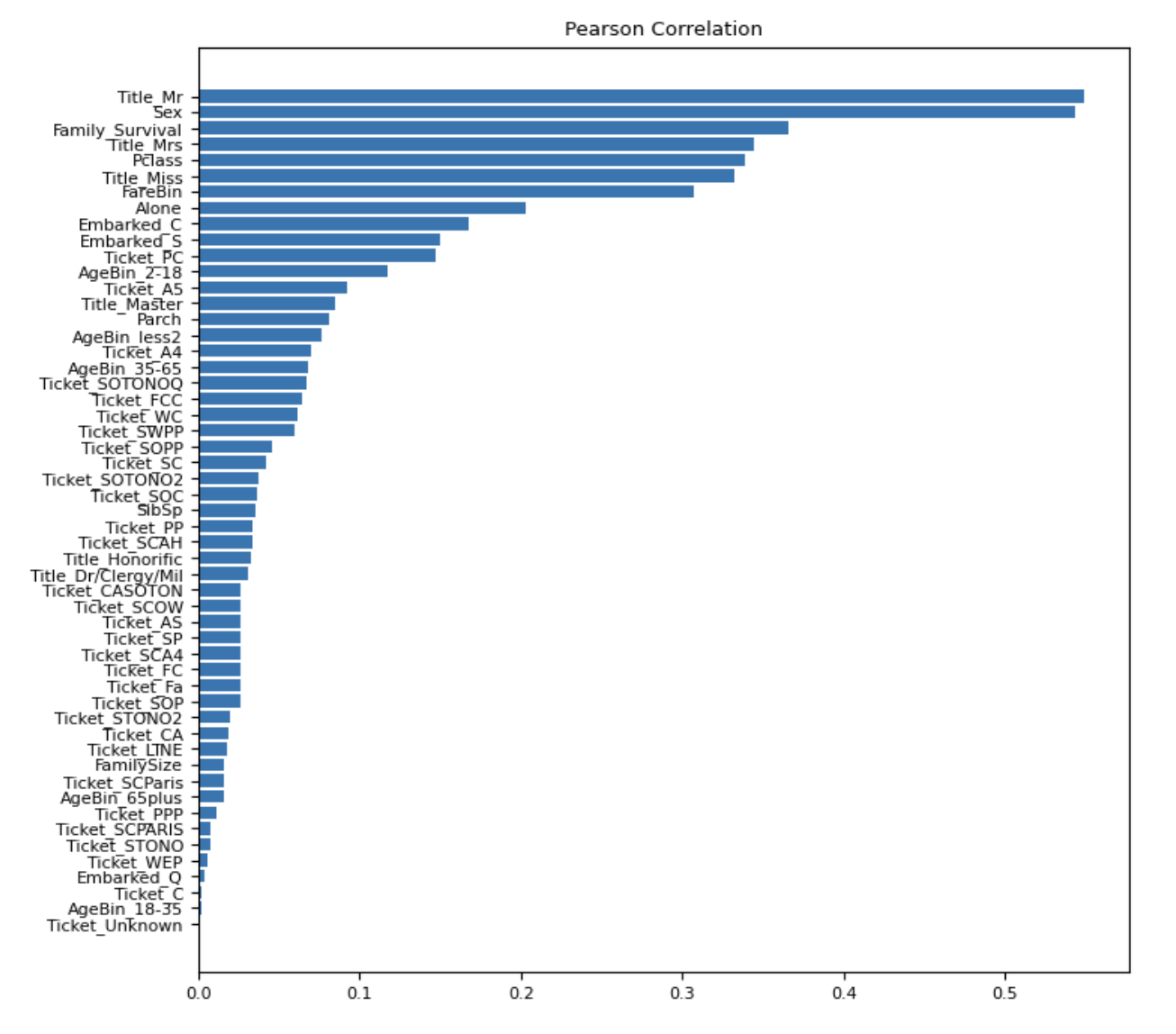
Спирмен против Пирсона

Несмотря на фундаментальные различия, между ними есть несколько ключевых отличий и применений:

1. Предположение о нормальности:
2. Корреляция Пирсона требует предположения о нормальности данных. Если это предположение не выполняется, оно становится менее надежным.
3. Корреляция Спирмена не требует нормального распределения данных и подходит как для нормально, так и для ненормально распределенных данных.
4. Чувствительность к выбросам:
5. Корреляция Пирсона более чувствительна к выбросам.
6. Корреляция Спирмена за счет рангов уменьшает влияние выбросов.
7. Тип данных:
8. Корреляция Пирсона лучше всего подходит для непрерывных данных.
9. Корреляция Спирмена может использоваться как с порядковыми данными (ранговыми), так и с непрерывными данными.
10. Характер взаимоотношений:
11. Корреляция Пирсона измеряет линейные отношения.
12. Корреляция Спирмена подходит как для линейных, так и для монотонных нелинейных связей.
13. Применение в машинном обучении:
14. В машинном обучении корреляция Пирсона полезна, когда данные нормально распределены и ожидается, что связь между переменными будет линейной.
<ли>

Корреляция Спирмена более универсальна для задач машинного обучения, особенно когда данные не подчиняются нормальному распределению или когда связь между переменными не является строго линейной.

Подводя итог, можно сказать, что выбор между коэффициентами корреляции Пирсона и Спирмена во многом зависит от характера данных и конкретных требований анализа. Для приложений машинного обучения корреляция Спирмена имеет тенденцию быть более универсально применимой, особенно при работе с реальными данными, которые могут не соответствовать предположениям о нормальности и линейности, требуемым корреляцией Пирсона.

Парная корреляция

Помимо фильтрации по значениям корреляции с целевой переменной крайне полезно проверить корреляцию признаков между собой для выявления избыточных данных. Для этого мы рассчитаем корреляции между каждым признаком с помощью функции corr() (без указания дополнительных параметров будет рассчитана корреляция Пирсона) и отобразим ее на тепловой карте.

import seaborn as sns
corr = train.corr()
plt.figure(figsize=(15,15))
sns.heatmap(corr, cmap="coolwarm")
plt.show()



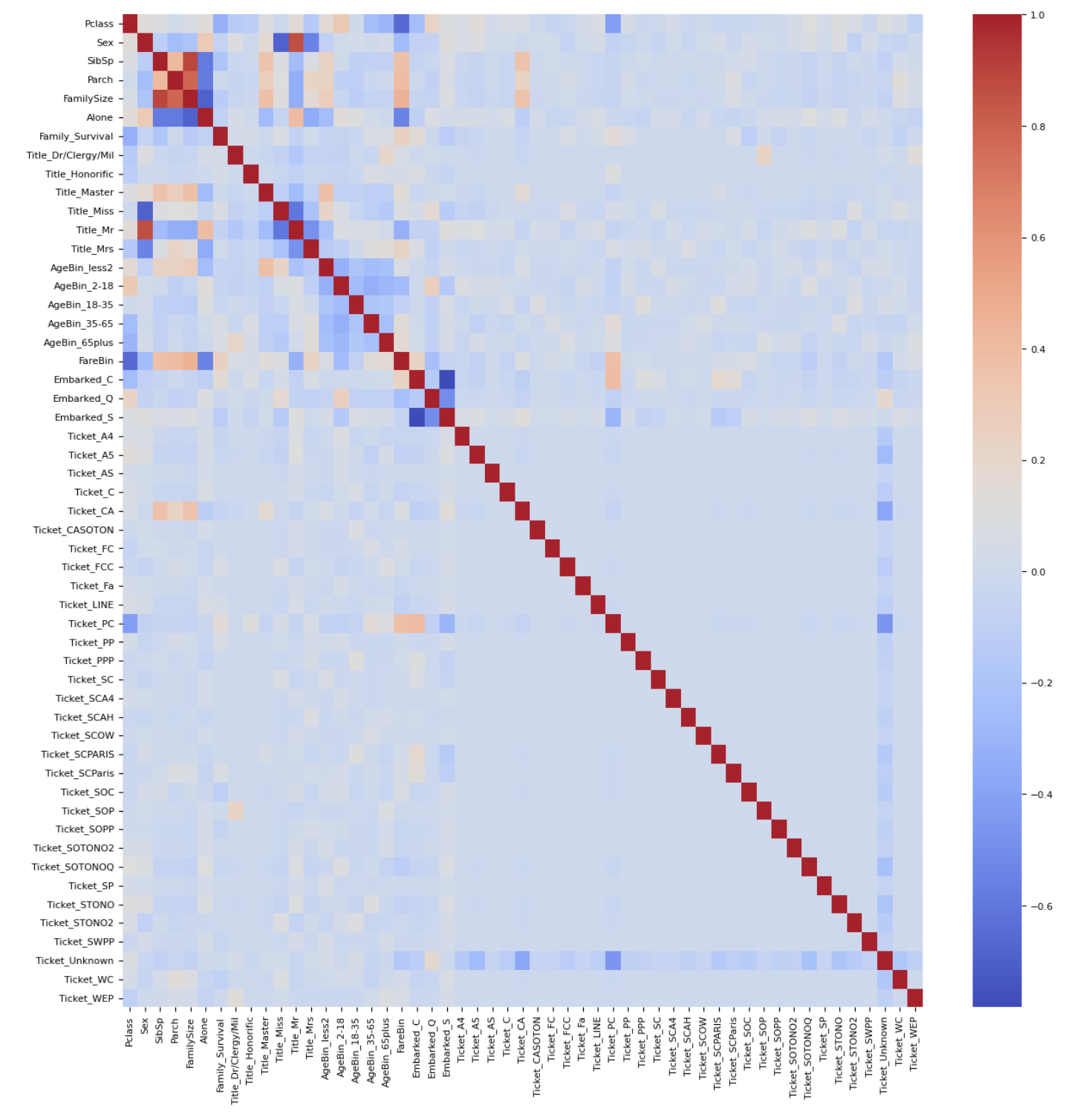
Как видно из тепловой карты, у нас есть признаки с довольно высокими абсолютными значениями корреляции. Поэтому из пар с высокими значениями мы можем выбрать только один признак.

Заключение

В этой вводной статье нашей серии о выборе функций мы начали изучать важную концепцию выбора наиболее подходящих функций для эффективного построения моделей в машинном обучении. Выбор функций имеет решающее значение для упрощения моделей, сокращения времени вычислений и повышения производительности модели за счет устранения проклятия размерности.

Мы коснулись различных подходов к выбору функций, включая фильтры, оболочки и встроенные методы, каждый из которых предлагает уникальные преимущества при анализе данных. В частности, методы фильтрации отличаются экономичным способом фильтрации большого количества функций. Они эффективно определяют ключевые взаимосвязи между функциями, не приспосабливая их к какой-либо конкретной модели, что делает их универсальным и важным инструментом на начальных этапах выбора функций.

Продолжая эту серию статей, мы будем углубляться в каждый подход, раскрывая его тонкости и приложения. Наше внимание будет сосредоточено на предоставлении краткого практического понимания искусства и науки выбора функций, гарантируя, что читатели будут хорошо подготовлены к решению задач оптимизации моделей в машинном обучении. Следите за обновлениями, чтобы получить более подробные сведения и рекомендации в следующих статьях этой серии.

---

Оригинал