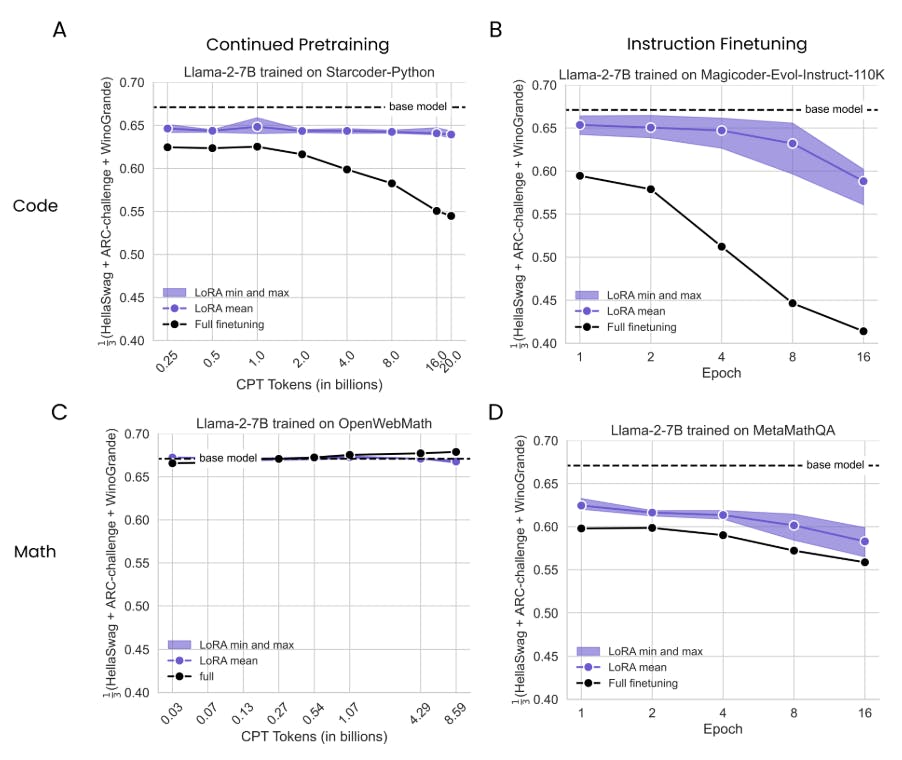
Лора не достигает полного создания в программировании и математических задачах
17 июня 2025 г.Таблица ссылок
Аннотация и 1 введение
2 фон
3 Экспериментальная настройка и 3,1 наборов данных для продолжения предварительной подготовки (CPT) и создания инструкций (IFT)
3.2 Измерение обучения с помощью кодирования и математических показателей (оценка целевой области)
3.3 Забыть метрики (оценка доменов источника)
4 Результаты
4.1 Lora Underperforms Полное создание в программировании и математических задачах
4.2 Лора забывает меньше, чем полное создание
4.3 Обмен на обучение
4.4 Свойства регуляризации Лоры
4.5 Полная производительность на коде и математике не изучает низкие возмущения
4.6 Практические выводы для оптимальной настройки LORA
5 Связанная работа
6 Обсуждение
7 Заключение и ссылки
Приложение
А. Экспериментальная установка
B. Поиски скорости обучения
C. Обучающие наборы данных
D. Теоретическая эффективность памяти с LORA для однократных и мульти-GPU настройки
4 Результаты
4.1 Lora Underperforms Полное создание в программировании и математических задачах
Мы сравниваем LORA и полную компанию после выполнения исчерпывающей скорости обучения для каждого метода, который, по нашему мнению, имеет решающее значение (Dettmers et al., 2024). Мы включаем результаты развертки скорости обучения на рисунке 8.
Мы выполняем анализ эффективности образца-то есть вычисляем метрики обучения в зависимости от того, что они наблюдаются-как для LORA, так и для полного искусства. Для IFT мы тренируем отдельные модели для 1, 2, 4, 8, 16 эпох. Для CPT мы манипулируем количеством уникальных токенов (0,25, 0,5, 1, 2, 4, 8, 16, 20 миллиардов), используя индивидуальные расписания по сокращению обучения. Мы тренируем шесть моделей LORA для каждого условия (3 целевых модуля [«Внимание», «MLP» и «все»] × 2 ранга [16, 256]).
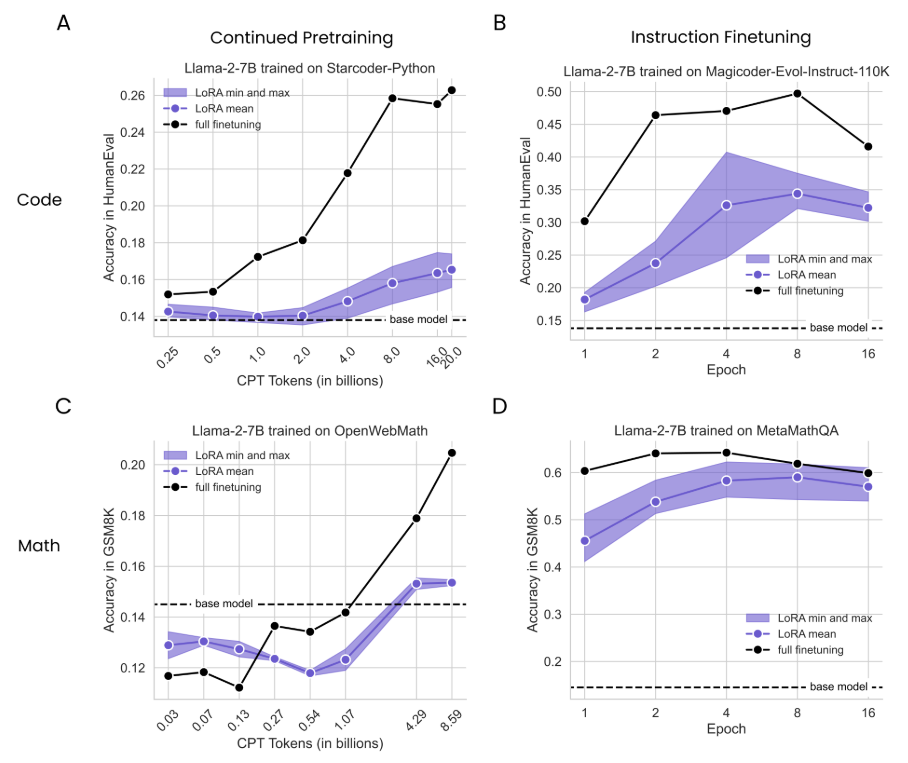
На рис. 2 мы суммируем производительность шести моделей LORA с их минимальной, средней и максимальной производительностью для каждой продолжительности обучения (в фиолетовом) и сравниваем их с полным созданием (сплошные черные линии) и базовой модели (пунктирная горизонтальная линия); Результаты дополнительно разбиты на конфигурацию LORA на рис. S2. Сначала отмечаем, что для обоих доменов IFT приводит к более значительным улучшениям по сравнению с CPT, что ожидается, потому что проблемы IFT более похожи на проблемы оценки (например, для кода, IFT достигает максимального гуманного проживания 0,50 против 0,26 для CPT).
ДляКод cpt(Рис. 2A), мы определяем значительный разрыв между полным созданием и Лорой, который растет с большим количеством данных. Лучшие лучшие пики Лоры в токенах 16b (ранга = 256, «все») с гуманом = 0,175, что примерно соответствует полному искусству с токенами 1B (Humaneval = 0,172). Полное создание достигает своего пикового гуманевала 0,263 при 20B токенах. ДляКод ift(Рис. 2B), наиболее эффективная LORA (R = 256, «все») достигает гуманевала = 0,407 в эпохе 4, осмысленно снижая полную производительность в эпохе 2 (гуманевл = 0,464) и при его пиковом балле HumaneVal 0,497 в 8 эпохах.Math Cpt(Рис. 2C) Результаты показывают, что обучение токенам 1B или меньше деградирует результаты GSM8K ниже базовой линии (GSM8K = 0,145). Улучшения появляются с большим количеством данных, где лучшая LORA (Rank = 256, «All») достигает GSM8K = 0,187 при 8,6 миллиарда токены, снижая полную производителя в 4,3 миллиарда токены (GSM8K = 0,191) и в 8,6 млрд. Токен (GSM8K = 0,230). Лора закрывается
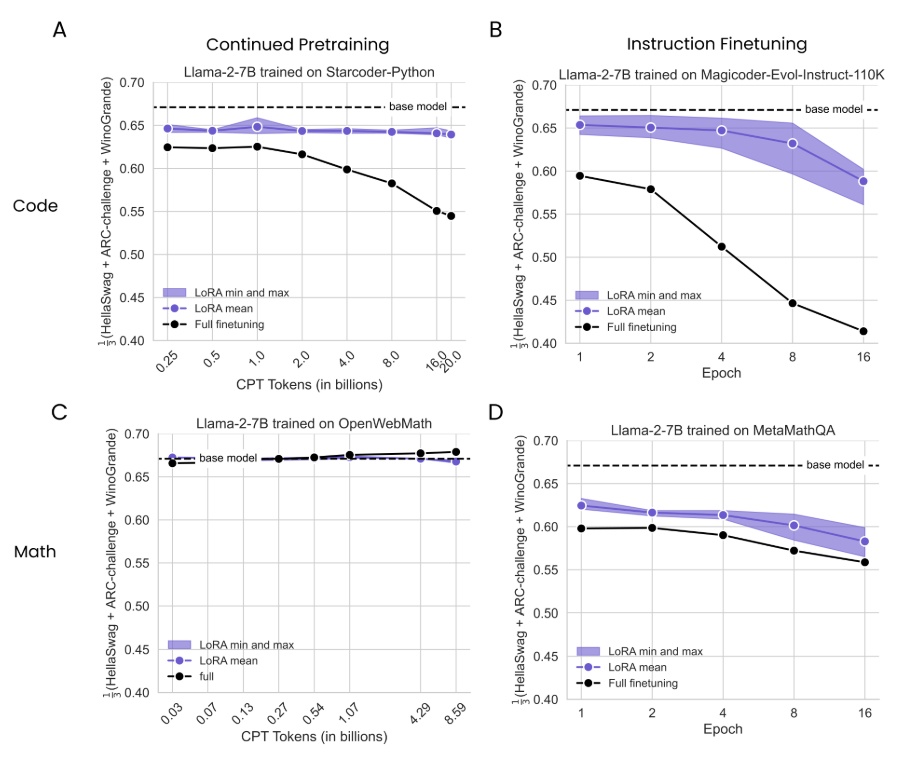
Большая часть разрыва с полным набором данных в математическом наборе данных IFT (рис. 2D). Тем не менее, Лора все еще остается менее эффективной выборкой. Lora (r = 256, «все») пика в 4 эпох (GSM8K = 0,622), в то время как полное создание достигает GSM8K = 0,640 в 2 эпохах и пиках в 4 эпохах, с GSM8K = 0,642. [6] Оба метода существенно превышают базовую модель. Мы предполагаем, что более мягкие пробелы здесь соответствуют меньшему сдвигу домена между математическими задачами и данными предварительного подготовки, отличающимися от больших сдвигов в коде.
Таким образом, через конфигурации LORA и продолжительность обучения, это все еще, по -видимому, не работает. Эти эффекты более выражены для программирования, чем математика. Для обоих доменов, создание инструкций приводит к большему повышению точности, чем продолжающаяся предварительная подготовка.
Авторы:
(1) Дэн Бидерман, Колумбийский университет и Databricks Mosaic AI (db3236@columbia.edu);
(2) Хосе Гонсалес Ортис, DataBricks Mosaic AI (j.gonzalez@databricks.com);
(3) Джейкоб Портес, DataBricks Mosaic AI (jportes@databricks.com);
(4) Mansheej Paul, DataBricks Mosaic AI (mansheej.paul@databricks.com);
(5) Филип Грингард, Колумбийский университет (pg2118@columbia.edu);
(6) Коннор Дженнингс, DataBricks Mosaic AI (connor.jennings@databricks.com);
(7) Даниэль Кинг, DataBricks Mosaic AI (daniel.king@databricks.com);
(8) Сэм Хейвенс, DataBricks Mosaic AI (sam.havens@databricks.com);
(9) Vitaliy Chiley, DataBricks Mosaic AI (vitaliy.chiley@databricks.com);
(10) Джонатан Франкл, DataBricks Mosaic AI (jfrankle@databricks.com);
(11) Коди Блакни, DataBricks Mosaic AI (Cody.blakeney);
(12) Джон П. Каннингем, Колумбийский университет (jpc2181@columbia.edu).
Эта статья есть
[6] Отметим, что в оригинальной метаматской статье сообщается о максимальной точности 0,665, когда (полностью) создает лама-2-7b в наборе данных Metamathqa. Мы приписываем это небольшим различиям в гиперпараметрах; Они тренировались в 3 эпохах с размером партии 128, используя оптимизатор ADAMW, скорость обучения 2E-5, разминка скорости обучения в 3%.
Оригинал

